Susceptibility assessment of precipitation-induced mass landslides based on optimal random forest model: Taking the extreme precipitation event in western Qinling mountains as an example
-
摘要:
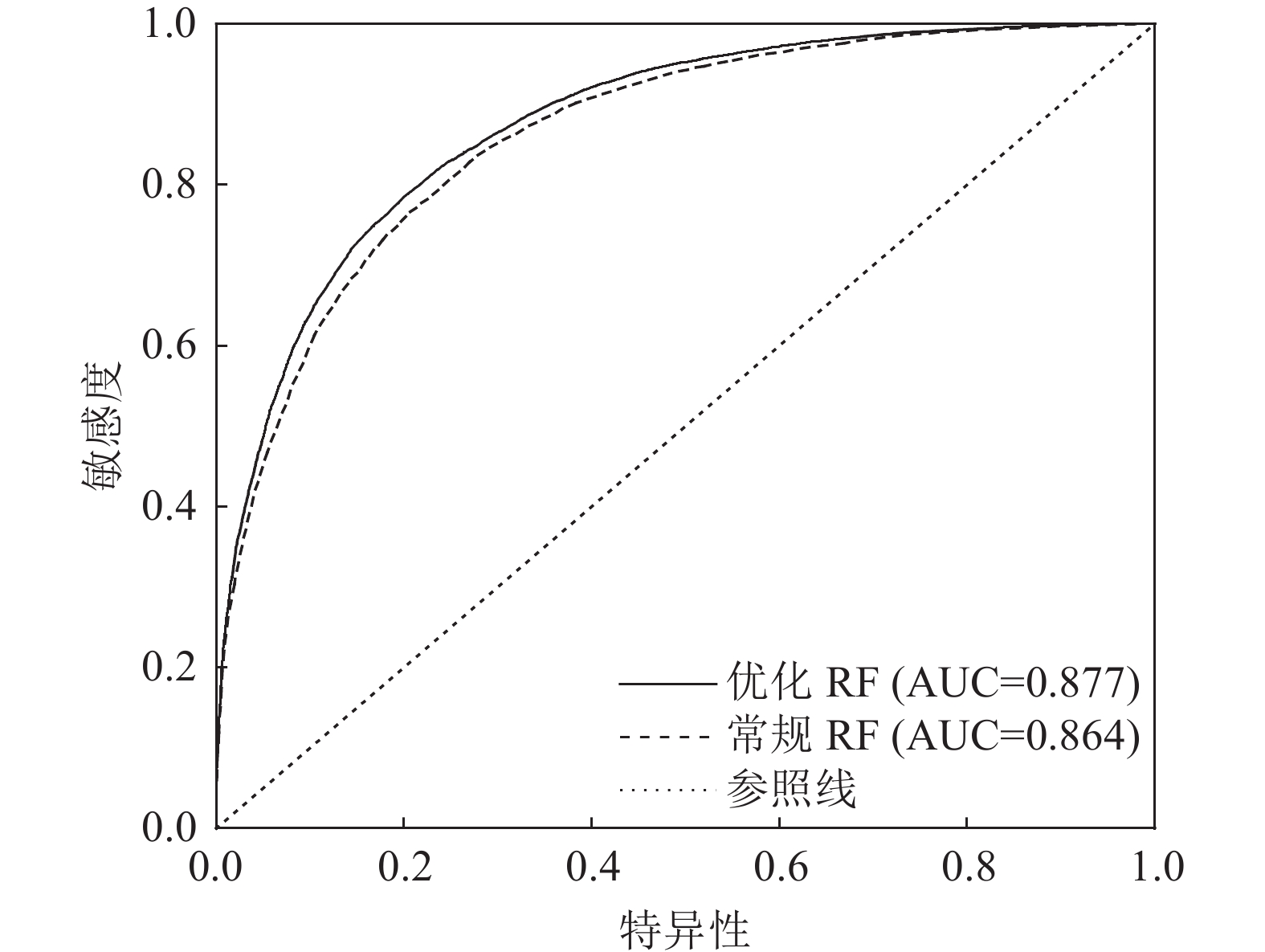
随机森林模型(RF)是在滑坡易发性评价中广泛应用的机器学习模型之一。针对制约随机森林模型评价应用质量的难点问题,以西秦岭山区娘娘坝镇极端降雨诱发的2万余处群发滑坡为例,从滑坡−非滑坡样本筛选方法、影响因子选取、联结方法应用和超参数优化4个方面开展了模型优化及与常规模型评价的对比研究。通过区域滑坡易发性评价和有效性比较可知,2种情形评价均取得理想结果,优化随机森林评价结果AUC(精度曲线下的面积)可达0.877,对比常规评价结果更优,表明该优化方法可以明显提升随机森林模型在区域降雨滑坡评价中的效果和学习效率,可为气候变化背景下极端降雨群发滑坡灾害易发性评估提供参考。
Abstract:Random forest model (RF) is one of the widely used machine learning models for landslide susceptibility assessment. Aiming at the difficult problems that restrict the application quality of random forest model assessment, taking more than 20000 extreme rainfall landslides induced by extreme rainfall in Niangniangba Town, western Qinling Mountains as an example, the model optimization and comparison with conventional model evaluation were carried out mainly from four aspects: landslide−non−landslide sample screening method, influence factor selection, coupling method application and hyper−parameter optimization. Based on the above optimization, the regional landslide susceptibility evaluation and effectiveness comparison of typical towns−Niangniangba Town are carried out. The evaluation of both situations has achieved ideal results. The optimized random forest evaluation result AUC can reach 0.877, which is better than the conventional assessment results. It shows that the optimization method can obviously improve the assessment effect and learning efficiency of random forest model in regional rainfall landslide, and can provide reference for the risk assessment of extreme rainfall landslide hazard under the background of climate change.
-
Key words:
- landslide /
- susceptibility /
- random forest /
- extreme rainfall /
- West Qinling
-

-
表 1 影响因子数据来源统计结果
Table 1. Statistical results of influence factor data sources
分类 序号 要素 致灾指示意义、数据说明及处理方法 地形地貌 1 坡度 指示坡体属性, ALOS DEM(12.5 m分辨率) 2 坡向 3 高程 4 平面曲率 5 剖面曲率 6 起伏度 地层岩性 7 地层岩性分区 指示斜坡岩土体的物理力学强度特征,基于1∶20万地质图(公开版) 河流 8 距一级河流距离 指示坡脚侵蚀及坡体的水文地质特征,使用1∶25万基础地理信息数据 9 距二级河流距离 道路 10 距一级道路距离 指示人类工程活动对斜坡破环的影响,使用1∶25万基础地理信息数据 11 距二级道路距离 前期有效降雨 12 前3日有效降雨 指示降雨有效入渗对滑坡发育的影响,通过气象台站降雨数据插值获取,1 km栅格 地质构造 13 距主要断层距离 指示地质构造对地质灾害的形成发展的影响,基于1∶20万地质图(公开版) 环境地质特征 14 土地利用类型 指示影响斜坡发育的环境地质特征,基于Landsat8遥感影响数据,30 m 15 修正归一化水体指数(MNDWI) 16 归一化建筑指数(NDBI) 17 归一化植被指数(NDVI) 表 2 影响因子量化结果
Table 2. Quantitative results of impact factors
类型 序号 分类 要素 实际取值范围 归一化取值 连续性 1 地形地貌 坡度 0~81° 0 ~ 1 2 坡向 0~360° 3 高程 1471~2030 m 4 平面曲率 −284~320 5 剖面曲率 −373~297 6 起伏度 0−171 m 7 河流 距一级河流距离 0~5594 m 8 距二级河流距离 0~2396 m 9 道路 距一级道路距离 0~4315 m 10 距二级道路距离 0~3819 m 11 前期有效降雨 前3日有效降雨 9−159 mm 12 地质构造 距主要断层距离 0~8047 m 13 环境地质特征 修正归一化水体指数(MNDWI) −0.40~0.27 14 归一化建筑指数(NDBI) −0.37~0.14 15 归一化植被指数(NDVI) −0.04~0.70 离散型 16 环境地质特征 土地利用类型 0~2.07(频率比) 17 地层岩性 地层岩性分区 0.09~1.50(频率比) 表 3 优化前后超参数对比
Table 3. Comparison of hyperparameters before and after optimization
参数名 优化参数值 默认参数值 训练用时 53 h 42 min 58 s 2 s 决策树数量 50 100 内部节点分裂的最小样本数 50 2 叶子节点的最小样本数 48 1 树的最大深度 12 10 叶子节点的最大数量 101 50 表 4 优化前后训练集结果对比
Table 4. Comparison of training set results before and after optimization
训练集 准确率 召回率 精确率 F1 优化RF 0.827 0.827 0.827 0.827 常规RF 0.794 0.794 0.794 0.794 表 5 滑坡易发性评价分区统计结果
Table 5. Landslide susceptibility assessment zoning statistical results
预测模型 易发性等级 高 中 低 非 分区面积/% 滑坡面积/% 分区面积/% 滑坡面积/% 分区面积/% 滑坡面积/% 分区面积/% 滑坡面积/% 优化RF 18.67 14.04 24.63 3.73 26.32 1.29 30.37 0.27 常规RF 17.47 13.56 24.37 2.98 20.91 1.62 37.25 0.39 -
[1] Abbas F, Zhang F, Ismail M, et al. 2023. Optimizing machine learning algorithms for landslide susceptibility mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A comparative study of baseline, bayesian, and metaheuristic hyperparameter optimization techniques[J]. Sensors (Basel, Switzerland), 23(15): 6843.
[2] Achu A L, Aju C D, Di N M, et al. 2023. Machine−learning based landslide susceptibility modelling with emphasis on uncertainty analysis[J]. Geoscience Frontiers, 14(6): 101657. doi: 10.1016/j.gsf.2023.101657
[3] Ado M, Amitab K, Maji A K, et al. 2022. Landslide susceptibility mapping using machine learning: A literature survey[J]. Remote Sensing, 14(13): 3029. doi: 10.3390/rs14133029
[4] Ahmad A, Farida M, Juita N, et al. 2023. Soil micromorphology for modeling spatial on landslide susceptibility mapping: A case study in Kelara subwatershed, Jeneponto Regency of South Sulawesi, Indonesia[J]. Natural Hazards, 118(2): 1445−1462. doi: 10.1007/s11069-023-06063-1
[5] Alvioli M M, Melillo F, Guzzetti M, et al. 2018. Implications of climate change on landslide hazard in Central Italy[J]. Sci. Total Environ., 630: 1528−1543. doi: 10.1016/j.scitotenv.2018.02.315
[6] Bui D, Tsangartos P, Nguyen T, et al. 2020. Comparing the prediction performance of a deep learning neural network model with conventional machine leaning models in landside susceptibility assessment[J]. Catena, 188: 104426. doi: 10.1016/j.catena.2019.104426
[7] Danika S, Edward M C, Sylvia H M, et al. 2019. A Mixed−Methods Evaluation of a gender affirmative education program for families of trans young people[J]. Journal of GLBT Family Studies, 16(1): 18−31.
[8] Deng H, Wu X T, Zhang W J, et al. 2022. Slope−unit scale landslide susceptibility mapping based on the random forest model in deep valley areas[J]. Remote Sensing, 14(17): 4245. doi: 10.3390/rs14174245
[9] Du G L, Zhang Y S, Iqbal J, et al. 2017. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China[J]. Journal of Mountain Science, 14(2): 249−268. doi: 10.1007/s11629-016-4126-9
[10] Guilherme G O, Luis F C, Laurindo A G, et al. 2019. Random forest and artificial neural networks in landslide susceptibility modeling: a case study of the Fão River Basin, Southern Brazil[J]. Natural Hazards, 99(2): 1049−1073. doi: 10.1007/s11069-019-03795-x
[11] Havenith H B, Torgoev A, Schlöge R, et al. 2015. Tienshan geohazards database: Landslide susceptibility analysis[J]. Geomorphology, 249: 2856.
[12] Huang F M, Chen J W, Liu W P, et al. 2022. Regional rainfall−induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold[J]. Geomorphology, 408: 108236. doi: 10.1016/j.geomorph.2022.108236
[13] Isidro C, Miguel A C, Francisco G, et al. 2019. A ROC analysis−based classification method for landslide susceptibility maps[J]. Landslides, 16(2): 265−282. doi: 10.1007/s10346-018-1063-4
[14] Jie D, Ali P Y, Abdelaziz M, et al. 2020. Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning[J]. Science of the Total Environment, 720: 137320. doi: 10.1016/j.scitotenv.2020.137320
[15] Ke W, Chang M W, Fang Qi, et al. 2012. Search of the most dangerous in slide slope stability analysis based on genetic algorithm[J]. Applied Mechanics and Materials, 1799: 166−169.
[16] Khan R, Yousaf S, Haseeb, A, et al. 2021. Exploring a Design of landslide monitoring system[J]. Complexity, 2021: 1−13.
[17] Li R, Huang S Y, Dou H Q. 2023. Dynamic risk assessment of landslide hazard for large−scale photovoltaic power plants under extreme rainfall conditions[J]. Water, 15(15): 2832. doi: 10.3390/w15152832
[18] Ma S Y, Shao X Y, Xu C, et al. 2023. Physically−based rainfall−induced landslide thresholds for the Tianshui area of Loess Plateau, China by TRIGRS model[J]. Catena, 233: 107499. doi: 10.1016/j.catena.2023.107499
[19] María C H, Laura P C, Iván L H, et al. 2023. Landslide susceptibility analysis on the vicinity of Bogotá−Villavicencio road (Eastern Cordillera of the Colombian Andes)[J]. Remote Sensing, 15(15): 3870. doi: 10.3390/rs15153870
[20] Reichenbach P M, Rossi B D, Malamud M M, et al. 2018. A review of statistically−based landslide susceptibility models[J]. Earth−Science Reviews 180: 60−91.
[21] Sun D L, Wen H J, Wang D Z, et al. 2020. A Random Forest Model of landslide susceptibility mapping based on Hyperparameter Optimization using bayes algorithm[J]. Geomorphology, 362: 107201.
[22] Tareq H M, Juhari M A, Abdul G R, et al. 2011. Landslide susceptibility assessment using frequency ratio model applied to an area along the E−W highway (Gerik−Jeli)[J]. American Journal of Environmental Sciences, 7(1): 47−56.
[23] Wen F, Xin S W, Yan B C, et al. 2017. Landslide susceptibility assessment using the certainty factor and analytic hierarchy process[J]. Journal of Mountain Science, 14(5): 906−925. doi: 10.1007/s11629-016-4068-2
[24] Yang H, Shi P, Quincey D. et al. 2023. A heterogeneous sampling strategy to model earthquake−triggered landslides[J]. Int. J. Disaster Risk Sci., 14(4): 636−648.
[25] Yao J, Qin S, Qiao S, et al. 2022. Application of a two−step sampling strategy based on deep neural network for landslide susceptibility mapping[J]. Bulletin of Engineering Geology and the Environment, 81: 1−20. doi: 10.1007/s10064-021-02521-x
[26] Yao X, Tham L, Dai F, et al. 2008. Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of Hong Kong, China[J]. Geomorphology, 101: 572−582. doi: 10.1016/j.geomorph.2008.02.011
[27] Youssef A M, Pourg H, Hamid R, et al. 2016. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia[J]. Landslides, 13(5): 839. doi: 10.1007/s10346-015-0614-1
[28] 郭飞, 赖鹏, 陈洋, 等. 2022. 不同环境因子联接方法对崩岗易发性评价的影响[J]. 水土保持通报, (425): 123−130.
[29] 郭飞, 赖鹏, 黄发明, 等. 2023. 基于知识图谱的滑坡易发性评价文献综述及研究进展[J/OL]. 地球科学, 1−33. [2024−05−14]. http://kns.cnki.net/kcms/detail/42.1874.P.20230713.1234.002.html.
[30] 郭富赟, 孟兴民, 黎志恒, 等. 2015. 天水市“7·25”群发性地质灾害特征及成因[J]. 山地学报, 33(1): 100−107.
[31] 黄发明, 殷坤龙, 蒋水华, 等. 2018. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 37(1): 156−167.
[32] 黄森. 2021. 天水市“7·25”群发性降雨滑坡灾害预警模型研究[D]. 西北大学硕士学位论文.
[33] 李霞, 宿星, 张满银, 等. 2023. 基于证据权法与多源数据的陇中生态脆弱区滑坡敏感性评价——以天水市为例[J]. 冰川冻土, 45(1): 67−79.
[34] 刘帅, 朱杰勇, 杨得虎, 等. 2023. 基于斜坡单元与随机森林模型的元阳县崩滑地质灾害易发性评价[J]. 中国地质灾害与防治学报, 34(4): 144−150.
[35] 孟晓捷, 张新社, 曾庆铭, 等. 2022. 基于加权信息量法的黄土滑坡易发性评价——以1∶5万天水市麦积幅为例[J]. 西北地质, 55(2): 249−259.
[36] 唐辉明, 鲁莎. 2018. 三峡库区黄土坡滑坡滑带空间分布特征研究[J]. 工程地质学报, 26(1): 129−136.
[37] 吴润泽, 胡旭东, 梅红波, 等. 2021. 基于随机森林的滑坡空间易发性评价: 以三峡库区湖北段为例[J]. 地球科学, 46: 321−330.
[38] 许强, 黄润秋, 李秀珍. 2004. 滑坡时间预测预报研究进展[J]. 地球科学进展, (3): 478−483.
[39] 殷跃平, 高少华. 2024. 高位远程地质灾害研究: 回顾与展望[J]. 中国地质灾害与防治学报, 35(1): 1−18.
[40] 周晓亭, 黄发明, 吴伟成, 等. 2022. 基于耦合信息量法选择负样本的区域滑坡易发性预测[J]. 工程科学与技术, 54(3): 25−35.
-




 下载:
下载: