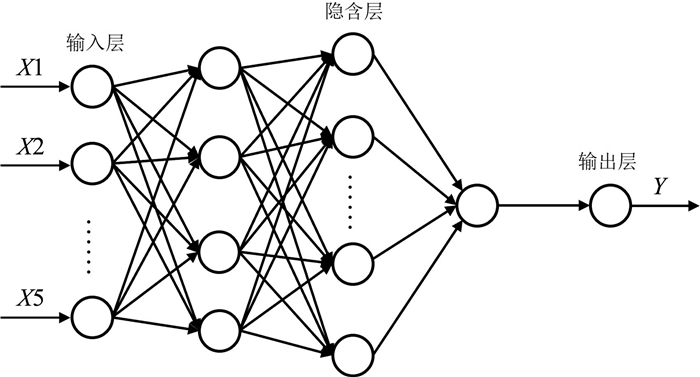
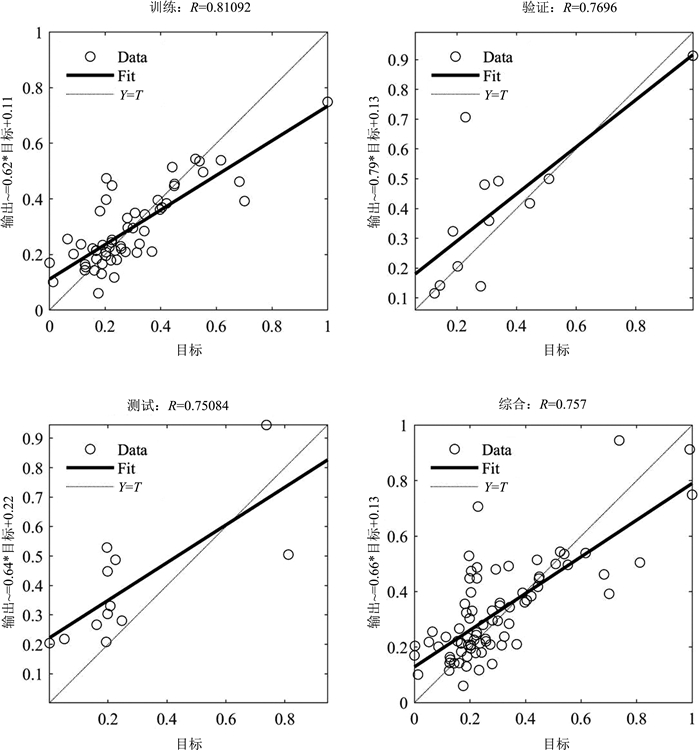
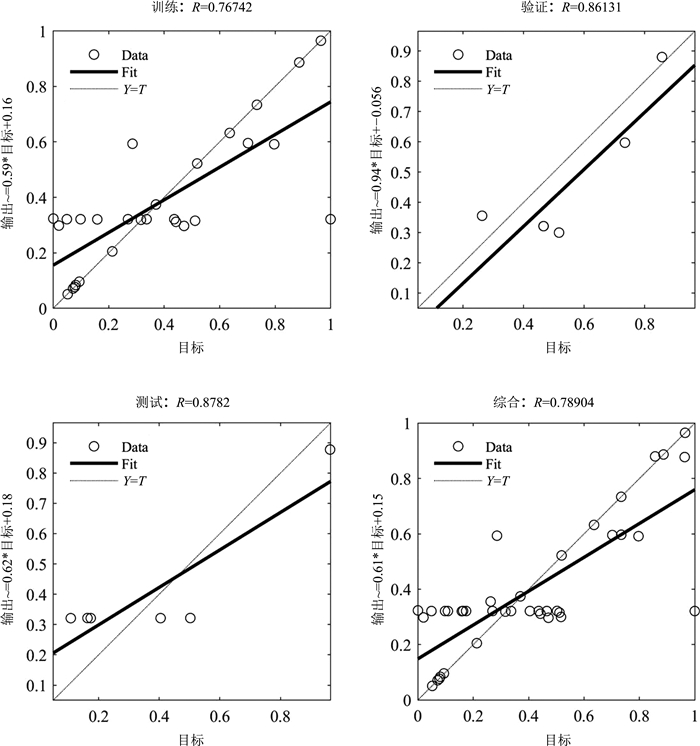
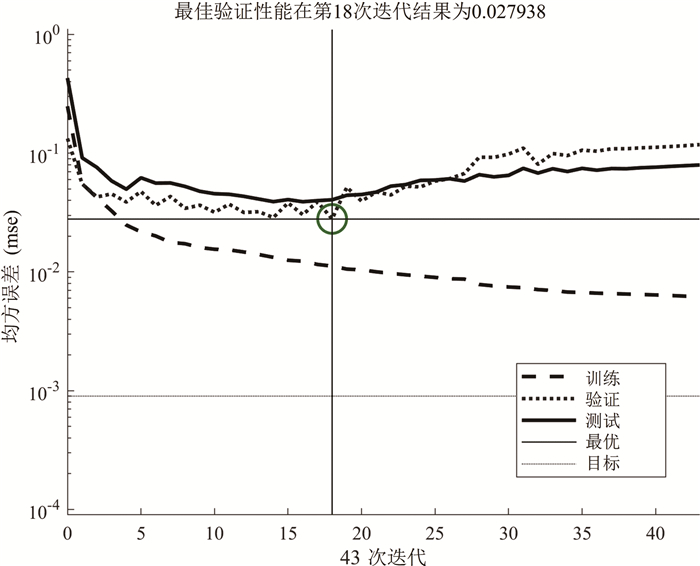
Research on landslide sliding distance prediction model based on multiple nonlinear regression and BP neural network
-
摘要:
滑坡灾害严重威胁着人类的生命财产安全, 对土地资源造成了一定影响。滑坡滑动距离直接表明了滑坡的冲击、堆积范围大小, 是估算滑坡受灾面积、评估滑坡潜在风险的重要参数, 也是滑坡防灾减灾工作中需要重点关注的指标。为了更准确高效地预测滑坡危害范围, 分别采用多元非线性回归和BP神经网络2种模型对影响滑坡滑动距离的因子进行了评估和建模, 并对天水地区的滑坡实例进行研究。研究结果表明, 2种模型均可用于滑坡滑动距离的预测。相较而言, BP神经网络的预测结果与实际情况有更高的拟合度, 准确性更高。
Abstract:Landslide disasters seriously threaten the safety of human life and property and have a certain impact on land resources. The landslide sliding distance directly indicates the impact and accumulation range size of landslides, which is an important parameter for estimating the affected area of landslides and assessing the potential risk of landslides and is also an indicator that needs to be focused on in landslide prevention and mitigation work. In order to predict the landslide hazard range more accurately and efficiently, this paper uses the theories of multivariate nonlinear regression and BP neural network to estimate the sliding distance of the landslide, respectively. And to study examples of landslides in the Tianshui region, the results show that both models can be used to predict landslide. Compared with the actual results, the BP neural network has a higher degree of fit and accuracy.
-
滑坡是自然界造成严重危害的自然灾害之一。由于中国的地形地貌情况较复杂、山坡丘陵多，滑坡成为严重的自然灾害。多年来，滑坡对人类生命安全和财产造成严重影响。国内外进行了很多滑坡预测的研究，以减轻滑坡造成的危害。由于滑坡的成因较复杂，受到多种因素的影响，传统的物理模型和线性方法对于预测滑坡距离还有一定的局限性，因此对非线性回归预测模型和BP神经网络预测模型进行了比较，发现BP神经网络具有更好的准确性。
滑坡的产生因素复杂，通常是在多种原因的共同作用下产生的，因此许多学者分析了滑坡空间分布与影响因素之间的关系，为编制滑坡灾害危险性区划图提供参考[1]。然而，除王兰民等[2]以93例黄土滑坡为例，提出了利用模糊信息模型预测黄土高原地震滑坡滑动距离的方法外，很少有研究者探讨各种因素对滑坡运动距离及其预测的有效性。
本次研究在非线性模型对天水地区滑坡预测的基础上，创造性地引入BP神经网络，旨在明确滑坡特征因子与滑动距离的关系，比较2种模型，探索提升模型精度，合理构建滑动距离预测模型，为滑坡危险性评价中滑坡危害范围的确定奠定基础。
1. 基本原理
1.1 多元非线性回归模型原理
当研究一个因变量Y与一个或多个自变量(X1~Xn) 之间的非线性关系时，可以使用非线性回归模型，并利用统计分析方法和函数对这种关系进行分析解读和形式化描述。非线性的最小二乘法是最常用的参数估计方法，该方法可以使用线性函数来逼近非线性函数，从而通过不断迭代这一过程得到参数的最优解[3]。因此可以采用该方法用于滑坡滑动距离的预测。
滑坡滑动距离受多种因素共同作用，假设滑坡滑动距离是影响因素的连续光滑函数，可表达为如下公式：
L=L(x1,x2,⋯,xn) (1) 式中：L为滑坡滑动距离，xi为滑坡滑动距离影响因素，其中i=1, 2，⋯，n。
将以上表达式在零点处Taylor展开，
L=L(x1,x2,⋯,xn)=L(0)+∑n(∂L∂xn)0xn+12∑l,n(∂2L∂xl∂xn)0xlxn+…+Rn(L) (2) 定义
Qn=(∂q∂xn)0 ，Qln=12(∂2q∂xl∂xn) 则上式可简化为
L=L(0)+∑nQnxn+∑l,nQlnxlxn+…+Rn(L) (3) 以上分析表明，当影响因素xn对滑坡滑动距离影响较大时，即同时存在线性与非线性影响，则需保留至强度的Taylor展开二次项，各因素对滑动距离的影响存在非线性，且2个因素间对滑动距离交叉影响，系数Qn、Qln为其影响程度；当需要保留展开的n次项时，n个不同因素对滑动距离交叉影响。系数Qn、Qln可在既有滑坡资料基础上，通过多元回归模型确定。
1.2 BP神经网络模型原理
BP神经网络是20世纪80年代发展起来的，网络结构简单，使用简单方便。BP神经网络采用的是非循环多级网络的训练算法，具有广泛的适用性，在1986年提出后，很快成为应用最广泛的多级网络算法。Robert Hecht-Nielsen证明，一个3层BP神经网络可以满足一般函数映射的要求，并且用有限的隐含层BP神经网络可以以任意精度逼近任意多变量函数[4]。
BP神经网络由输入层、隐含层、输出层组成。其训练方式是采用有导师学习。一般地，输入样本集为{X，Y}；X为输入向量，Y为X对应的理想输出向量。BP神经网络接受样本数据的神经元为输入层，输出最终结果的为输出层，隐含于输入层和输出层之间的称为隐含层。BP神经网络的有导师学习过程就是对其的训练过程。也就是将由样本向量构成的样本集合输入到网络中后，按照一定的方式去调整神经元之间的联接权，使得网络能将样本集的内涵以联接权矩阵的方式存储起来，从而使得网络在接受输入时，可以给出适当的输出。网络训练寻优采用的是最速下降法。对每个神经元来说，其输入为：
net=XWX=(x1,x2,⋯,xn);W=(w1,w2,⋯,wn) (4) 式中：X为输入向量；W为联接权向量。隐含层单个神经元(节点)激活函数(输出)采用S形函数：
O=f(net)=a+b1+exp(−dnet) (5) 网络的训练过程主要包括信息的正向传播和误差反向传播2个反复的过程。在正向传播过程中，前一层的输入经过加权计算后作为后一层的输入，即XW。误差反向传播学习是指根据实际输出Op和理想输出Xp的差，以极小化误差的方式调整权矩阵，最终使误差控制在一定的要求范围内。第p个样本误差可描述为：
Ep=12m∑j=1(ypj−Opj)2 (6) 式中：yp为期望输出；Qp为网络输出；m为输出节点数。
样本集总误差为E=∑Ep，直到求出满足要求的样本为止。
2. 实例分析
天水市位于甘肃省东南部，渭河上游。总面积1.4325×104 km2，呈条带状展布，为典型的山间河谷盆地型。天水市地形高低差较大，并且绝大部分是黄土丘陵区，黄土覆盖较厚，因特殊的地质构造、岩土性质影响，地质环境十分脆弱，滑坡频发，降雨和地震的影响引起的滑坡占90%，并且常有新老滑坡相互叠加的情况，毗邻相连(图 1)。
图 1. 研究区地理位置及样地分布Figure 1. The geographical location and sample land distribution of the study area近年，天水市发生多起滑坡灾害，其中1990年因降雨发生的滑坡非常严重，当日的最大降水量达到113 mm，导致发生了20多处滑坡，将近200×104 m3的黄土滑坡在十几秒内突然快速移动了约150 m，此次自然灾害发生在一家工厂中，6个主体车间被摧毁，多种材料成本被压埋，生产设施被摧毁，造成经济损失高达2000多万元，因为停电的原因，工人都不在工厂才幸免于难，本次滑坡是天水市乃至整个甘肃省史上造成经济损失最严重的一次滑坡事故[5]。
2.1 数据来源
本次实验的数据以中国地质科学院地质力学研究所的历史滑坡灾害点及环境因子数据的收集为例，收集到空间分辨率为25 m×25 m的数字高程(DEM)栅格图、天水市历史滑坡灾害点，以及在中国科学院资源环境信息中心收集到的空间分辨率为1 km的归一化植被指数栅格图，使用ArcGIS进行相关数据的提取，共得到192条滑坡样本信息，分别采用一定比例作2种模型的训练、验证和预测。滑坡部分样本信息如表 1所示。
表 1. 滑坡样本信息Table 1. Landslide sample information滑坡类型 序号 面积(S)/m2 滑坡高差(ΔH)/m 滑坡平面形态 剖面曲率 实测水平滑动距离/m 地震型滑坡 1 3714.65 49.00 8.57 -0.16 114.08 2 4340.20 67.00 0.67 0.01 123.17 3 3682.84 37.00 0.24 -0.13 103.61 4 3083.52 23.00 1.50 -0.07 92.85 5 2591.62 10.00 9.80 -0.14 78.32 6 205537.00 96.15 2.40 0.01 579.50 7 46081.19 117.55 2.78 0.04 266.49 8 2230.50 5.00 5.38 -0.01 71.59 9 1521.04 5.00 2.50 0.66 65.05 10 2021.91 8.00 3.90 -0.52 67.43 降雨型滑坡 1 364142.40 195.31 2.66 -0.00 848.98 2 69610.23 84.35 7.10 0.61 378.90 3 293670.00 139.79 2.78 -0.44 751.93 4 246494.90 143.72 9.41 0.01 664.15 5 232660.70 148.89 2.64 0.09 798.40 6 205327.20 134.00 2.93 0.06 674.40 7 192072.60 229.52 4.02 -0.13 658.76 8 153099.00 169.30 9.80 -0.32 560.31 9 129207.60 333.89 4.39 -0.25 568.51 10 85299.35 213.01 5.39 0.09 402.65 | Show Table
DownLoad:
CSV
2.2 影响因子
影响滑坡滑动距离的因素有很多，历年来学者也在不断地对滑坡的影响因子，如滑坡前后缘高差、滑坡面积、滑坡坡度、滑坡等价摩擦系数、滑坡平面形态、地形地貌和植被覆盖率等进行了研究[6]。滑坡前后缘高差可以控制到滑坡的质心位置，直接对滑坡的大小产生影响；滑坡体积和滑坡的滑动距离具有正相关的影响；根据滑坡平面形态的不同，对滑坡的运动也产生不同的影响，平面较狭长的滑坡，其滑动距离较远，宽展的滑坡往往滑动的距离较小；滑坡的等价摩擦系数指的是滑坡滑动的水平滑距和垂直距离的比值，可以用来衡量地貌因素对滑坡运动性能的阻止指标[7-10]。
3. 建模与验证
3.1 模型变量选取
自变量包括地质因子和环境因子，根据滑坡滑动距离与地质因子、环境因子之间的相关性并参考相关文献[7-10]，提取滑坡前后缘高差、滑坡面积、滑坡坡度、斜坡等价摩擦系数、滑坡长宽比、滑坡剖面曲率、植被覆盖度等，使用Matlab分别对各因子进行拟合，得到了各个因子的相关方程和相关系数，为进一步确定模型变量奠定基础。由表 2可见，当限定某一类滑坡时，滑动距离与滑坡各要素之间存在明显的线性或非线性相关性，而一旦滑坡类型不同，即使其具有相似的外部环境，滑动距离与滑坡各要素之间的相关性也会迅速降低。因此，需要根据滑坡类型建立相应的滑坡滑动距离预测模型。
表 2. 单因素滑坡要素线性相关计算结果Table 2. Calculation results of the linear correlation of single factor landslide elements降雨型滑坡 地震型滑坡 相关方程 相关系数 相关方程 相关系数 滑坡前后缘高差(ΔH) y=25.38x0.5654 0.4702 y=0.011x2-0.9985x + 306.08 0.6266 滑坡面积(S) y = 0.4344x0.5997 0.8357 y = 1.6571x0.4771 0.8312 滑坡坡度(i) 0.0536 0.0328 斜坡等价摩擦系数(μ=H/L) 0.0588 0.1272 滑坡平面形态(长宽比γ) y= 99.602x + 557.27 0.5752 y=379.5x+432.76 0.5378 地形地貌(平面曲率K) 0.5170 0.1490 植被覆盖 0.3870 0.0900 | Show TableDownLoad:
CSV
3.2 多元非线性回归模型的建立与求解验证
根据前述分析，地震滑坡滑动距离的影响因素按相关系数大小排序分别为滑坡面积(0.8312)、滑坡高差(0.6266)、滑坡平面形态(0.5378)、地形地貌(0.149)、滑坡坡度(0.171)、斜坡等价摩擦系数(0.1272)和植被覆盖(0.090)。故可认为，影响研究区地震滑坡滑动距离的主要因素有滑坡面积、滑坡高差、滑坡平面形态，可作为采用多元非线性回归模型估测地震滑坡滑动距离的指标。地形地貌、滑坡坡度、斜坡等价摩擦系数和植被覆盖率为次要因素。
影响降雨滑坡滑动距离的因素按影响程度强弱排序分别为滑坡面积(0.8357)、滑坡平面形态(0.5752)、地形地貌(0.517)、滑坡高差(0.4702)、植被覆盖(0.387)、滑坡坡度(0.133)和斜坡等价摩擦系数(0.0588)。故可认为影响研究区地震滑坡滑动距离的主要因素有滑坡面积、滑坡平面形态、地形地貌、滑坡高差，可作为采用多元非线性回归模型估测地震滑坡滑动距离的指标。而植被覆盖率、滑坡坡度和斜坡等价摩擦系数为次要因素。
为探讨各因素对滑坡滑动距离影响的非线性作用，取滑坡数据进行分析，以上述因子为自变量，通过变量代换对非线性项线性化后，利用多元线性模型[10]进行分析。发现在主要的影响因素中滑坡面积和滑坡相对高差是2个相关性最大的因素，故保留了相关系数较高的影响因子，得到拟合结果如下：
fL={−116.819+0.002S+0.539ΔH−0.003ΔH2+23.187ln(S)(R2=0.960),T=地震−173.476+4.258S0.43+3.089ΔH0.47(R2=0.812),T=降雨 (7) 式中：S为滑坡面积；ΔH为滑坡相对高差；T为诱发滑坡类型。
经方差分析及显著性检验可得：地震型滑坡D-W=2.077，降雨型滑坡D-W=1.625(表 3)，表明数据满足独立性；F地震=399.510>F0.05(F0.05=2.61)，F降雨=132.098>F0.05，P=0.000 < 0.05，模型有统计学意义，说明在0.05检验水平上，该模型有显著意义，故判定该多元非线性回归方程有效，可用于生产实践。
表 3. 多元相关系数Table 3. Multiple correlation coefficient模型 R R2 调整后R2 标准差 德宾-沃森 地震诱发 0.980a 0.960 0.957 49.037 2.077 降雨诱发 0.901a 0.812 0.806 114.208 1.625 | Show TableDownLoad:
CSV
采用建立的多元非线性回归方法模型进行滑坡范围预测检验。基于实地测量的数据，随机选取天水市10个地震滑坡、10个降雨型滑坡完整样本信息进行验证。将滑坡信息带入公式(7)，计算所得滑动距离与实际滑动距离进行比较，分析其相对误差(表 4)。由表 4可知，对于地震诱发的滑坡，非线性模型最小相对误差为0.61%，最大相对误差为11.98%；对于降雨诱发的滑坡，非线性模型最小相对误差为0.37%，最大相对误差为12.16%。因此，采用此多元非线性回归模型分别预测地震、降雨诱发滑坡滑动距离是合理的。
表 4. 非线性回归模型检验结果Table 4. Nonlinear regression model test results滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 地震 1 114.0800 100.4163 11.98% 2 123.1700 108.7141 11.74% 3 103.6100 96.7813 6.59% 4 92.8500 86.4384 6.91% 5 78.3200 75.7050 3.34% 6 579.5030 602.0008 3.88% 7 266.4900 246.2345 7.60% 8 71.5850 69.0334 3.56% 9 65.0480 58.7377 9.70% 10 67.4300 67.8396 0.61% 降雨 1 848.9849 911.8369 7.40% 2 378.9010 366.0614 3.39% 3 751.9303 813.8553 8.24% 4 664.1453 744.9368 12.16% 5 798.3964 723.7249 9.35% 6 674.3973 676.9118 0.37% 7 658.7645 662.6150 0.58% 8 560.3139 583.3253 4.11% 9 568.5081 545.4595 4.05% 10 402.6479 426.6198 5.95% | Show TableDownLoad:
CSV
综上所述，多元非线性回归模型能够用于描述各种因素对滑坡滑动距离的影响。当考虑各因素对滑坡滑动距离的非线性影响时，保留至Taylor展开二次项，即可利用模型描述各因素对滑坡滑动距离的影响。
3.3 神经网络模型的建立与求解验证
以天水市实地调查的数据用于本次实验，经处理共得到192条滑坡样本信息，采用134条数据用于训练样本，30条数据用于验证，28条数据用于测试，以及总数据量的70%为训练样本，15%为验证数据，15%为测试数据计算。滑动距离的预测涉及到多个环境变量的影响，并且各个影响因素与最终的滑动距离之间呈现出非线性的关系，实验验证表明，建立一个5层的神经网络模型能够较准确的预测滑坡的滑动距离，其中隐含层为3层。输入变量为回归模型中筛选出的5个相关系数较高的自变量，输出的结果对应研究区滑坡滑动距离实测值，该结构的训练、验证和预测的均方差误差均为最小。图 2为本实验的BP神经网络拓扑图。隐含层与输出层传递函数分别采用常用的Sigmoid型可微函数Logsig、Tansig和线性传递函数Purelin，网络训练函数采用Levenberg-Marquardt的BP算法训练函数Trainlm，网络最大训练次数为1000次，学习速率为0.01，目标误差选取0.9×10-4与隐含层神经元个数进行组合训练网络。通过对隐含层神经元个数及目标误差的每个不同组合进行训练，得到预测值与实测值的相对误差，预测值与实测值相对误差越小，网络训练结果越好[11-16]。
利用Matlab的神经网络工具箱编程将数据划分为训练数据、验证数据和测试数据，当训练数据参与训练时，其他两部分不参与训练，用于验证。随着训练次数的不断增加，测试的误差将不断变小。图 3、图 4分别为降水和地震型滑距预测的训练、验证和测试的结果图。
图 3. 训练、验证和测试的结果图(降雨型)Figure 3. Training, validation and testing results(rainfall pattern)
图 4. 训练、验证和测试的结果图(地震型)Figure 4. Training, validation, and testing results(seismic pattern)利用上述BP神经网络算法，对降雨型滑坡进行迭代寻优计算，最优均方差出现的时间与值如图 5所示。从图 5可知，最优均方误差出现在第18次迭代，根据第18次迭代，得到40组降雨型滑坡数据的滑距预测。同理，对地震型滑坡进行迭代寻优计算，最优均方差出现的时间与值如图 6所示。从图 6可知，最优均方误差出现在第40次迭代，根据第40次迭代，得到24组降雨型滑坡数据的滑距预测。
图 5. BP神经网络迭代训练寻优过程图(降雨型)Figure 5. BP neural networkiterative training optimization process(rainfall pattern)
图 6. BP神经网络迭代训练寻优过程图(地震型)Figure 6. BP neural network iterative training optimization process(seismic pattern)该模型采用相对误差和平均相对误差评价模型精度，将滑坡信息带入BP神经网络模型，计算所得滑动距离与实际滑动距离进行比较，分析其相对误差(表 5)。对于地震诱发滑坡，BP神经网络模型最小相对误差为0.47%，最大相对误差为10.05%；对于降雨诱发滑坡，BP神经网络模型最小相对误差为0.19%，最大相对误差为8.95%。因此，采用此BP神经网络模型分别预测地震、降雨诱发滑坡滑动距离是合理的。
表 5. BP神经网络模型模型检验结果Table 5. BP neutral network model test results滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 地震 1 601.1812 613.0617 1.98% 降雨 1 422.6054 419.8734 -0.65% 2 776.7570 783.4776 0.87% 2 522.1985 512.9397 -1.77% 3 675.6853 607.7622 -10.05% 3 204.6307 205.0255 0.19% 4 541.9784 545.0218 0.56% 4 280.4112 278.6681 -0.62% 5 638.5164 594.7821 -6.85% 5 318.2101 319.4857 0.40% 6 627.1131 577.6841 -7.88% 6 362.5568 365.213 0.73% 7 1132.0020 1034.372 -8.62% 7 182.6633 178.6214 -2.21% 8 790.7921 787.0566 -0.47% 8 293.9445 296.3856 0.83% 9 761.6214 733.1141 -3.74% 9 379.9835 413.9774 8.95% 10 669.9125 647.8153 -3.30% 10 254.1331 264.9736 4.27% | Show TableDownLoad:
CSV
根据多元非线性回归方程模型和BP神经网络模型预测得到的预测滑动距离和实测的水平滑动距离的比较，笔者分别计算多元非线性回归方程模型和BP神经网络模型的平均相对误差并进行了比较，结果如表 6所示。
表 6. 平均相对误差Table 6. Average relative error滑坡类型 多元非线性回归模型 BP神经网络模型 地震 6.59% 4.43% 降雨 5.56% 2.06% | Show TableDownLoad:
CSV
通过表 6可以看出，多元非线性回归模型和BP神经网络模型在预测滑坡的滑动距离方面都表现出不错的预测效果。但相对来说，BP神经网络的预测准确率稍高于多元非线性回归模型的预测准确度。
4. 结论
精确有效地预测出滑坡的滑动距离对于减轻滑坡造成的人员伤亡和财产损失是十分重要的，也是需要不断探索和研究的方向。本文提出了采用多元非线性回归和BP神经网络模型2种方法对滑坡距离进行预测；通过实验对相关数据进行拟合和预测，分别拟合预测了地震型滑坡和降雨型滑坡；对比多元非线性回归和BP神经网络2种模型的预测结果，可以得出，BP神经网络模型的预测相对于多元非线性回归模型来说误差较小。实验结果表明，2种方法都有较好的拟合效果和预测能力，均可用于滑坡滑距的预测。但由于数据本身原因，在非线性回归模型的最终拟合函数中只考虑了滑坡相对高差和滑坡面积2个因素。在接下来的工作中，随着数据的不断完善，会进一步验证算法的可行性。
-
表 1 滑坡样本信息
Table 1. Landslide sample information
滑坡类型 序号 面积(S)/m2 滑坡高差(ΔH)/m 滑坡平面形态 剖面曲率 实测水平滑动距离/m 地震型滑坡 1 3714.65 49.00 8.57 -0.16 114.08 2 4340.20 67.00 0.67 0.01 123.17 3 3682.84 37.00 0.24 -0.13 103.61 4 3083.52 23.00 1.50 -0.07 92.85 5 2591.62 10.00 9.80 -0.14 78.32 6 205537.00 96.15 2.40 0.01 579.50 7 46081.19 117.55 2.78 0.04 266.49 8 2230.50 5.00 5.38 -0.01 71.59 9 1521.04 5.00 2.50 0.66 65.05 10 2021.91 8.00 3.90 -0.52 67.43 降雨型滑坡 1 364142.40 195.31 2.66 -0.00 848.98 2 69610.23 84.35 7.10 0.61 378.90 3 293670.00 139.79 2.78 -0.44 751.93 4 246494.90 143.72 9.41 0.01 664.15 5 232660.70 148.89 2.64 0.09 798.40 6 205327.20 134.00 2.93 0.06 674.40 7 192072.60 229.52 4.02 -0.13 658.76 8 153099.00 169.30 9.80 -0.32 560.31 9 129207.60 333.89 4.39 -0.25 568.51 10 85299.35 213.01 5.39 0.09 402.65
下载: 导出CSV
表 2 单因素滑坡要素线性相关计算结果
Table 2. Calculation results of the linear correlation of single factor landslide elements
降雨型滑坡 地震型滑坡 相关方程 相关系数 相关方程 相关系数 滑坡前后缘高差(ΔH) y=25.38x0.5654 0.4702 y=0.011x2-0.9985x + 306.08 0.6266 滑坡面积(S) y = 0.4344x0.5997 0.8357 y = 1.6571x0.4771 0.8312 滑坡坡度(i) 0.0536 0.0328 斜坡等价摩擦系数(μ=H/L) 0.0588 0.1272 滑坡平面形态(长宽比γ) y= 99.602x + 557.27 0.5752 y=379.5x+432.76 0.5378 地形地貌(平面曲率K) 0.5170 0.1490 植被覆盖 0.3870 0.0900
下载: 导出CSV
表 3 多元相关系数
Table 3. Multiple correlation coefficient
模型 R R2 调整后R2 标准差 德宾-沃森 地震诱发 0.980a 0.960 0.957 49.037 2.077 降雨诱发 0.901a 0.812 0.806 114.208 1.625
下载: 导出CSV
表 4 非线性回归模型检验结果
Table 4. Nonlinear regression model test results
滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 地震 1 114.0800 100.4163 11.98% 2 123.1700 108.7141 11.74% 3 103.6100 96.7813 6.59% 4 92.8500 86.4384 6.91% 5 78.3200 75.7050 3.34% 6 579.5030 602.0008 3.88% 7 266.4900 246.2345 7.60% 8 71.5850 69.0334 3.56% 9 65.0480 58.7377 9.70% 10 67.4300 67.8396 0.61% 降雨 1 848.9849 911.8369 7.40% 2 378.9010 366.0614 3.39% 3 751.9303 813.8553 8.24% 4 664.1453 744.9368 12.16% 5 798.3964 723.7249 9.35% 6 674.3973 676.9118 0.37% 7 658.7645 662.6150 0.58% 8 560.3139 583.3253 4.11% 9 568.5081 545.4595 4.05% 10 402.6479 426.6198 5.95%
下载: 导出CSV
表 5 BP神经网络模型模型检验结果
Table 5. BP neutral network model test results
滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 滑坡类型 序号 实测水平滑动距离/m 模型计算得滑动距离/m 误差 地震 1 601.1812 613.0617 1.98% 降雨 1 422.6054 419.8734 -0.65% 2 776.7570 783.4776 0.87% 2 522.1985 512.9397 -1.77% 3 675.6853 607.7622 -10.05% 3 204.6307 205.0255 0.19% 4 541.9784 545.0218 0.56% 4 280.4112 278.6681 -0.62% 5 638.5164 594.7821 -6.85% 5 318.2101 319.4857 0.40% 6 627.1131 577.6841 -7.88% 6 362.5568 365.213 0.73% 7 1132.0020 1034.372 -8.62% 7 182.6633 178.6214 -2.21% 8 790.7921 787.0566 -0.47% 8 293.9445 296.3856 0.83% 9 761.6214 733.1141 -3.74% 9 379.9835 413.9774 8.95% 10 669.9125 647.8153 -3.30% 10 254.1331 264.9736 4.27%
下载: 导出CSV
表 6 平均相对误差
Table 6. Average relative error
滑坡类型 多元非线性回归模型 BP神经网络模型 地震 6.59% 4.43% 降雨 5.56% 2.06%
下载: 导出CSV
-
[1] 钟秀梅, 李伟利, 袁中夏, 等. 地震作用下天水市区滑坡危险区划研究[J]. 国际地震动态, 2019, (8) : 118-119. https://www.cnki.com.cn/Article/CJFDTOTAL-GJZT201908096.htm
[2] 王鼐, 王兰民, 王谦, 等. 黄土高原地震作用下黄土滑坡滑距预测方法[J]. 地震工程学报, 2016, 38(4) : 533-540. doi: 10.3969/j.issn.1000-0844.2016.04.0533
[3] Mahaboob B, Venkateswarlu B, Mokeshrayalu G, et al. A different approach to estimate nonliner regression model using numerical methods[C]//Materials Science & Engineering Conference Series. Materials Science and Engineering Conference Series, 2017.
[4] 张保生, 纪昌明, 陈森林. 多元线性回归和神经网络在水库调度中的应用比较研究[J]. 中国农村水利水电, 2004, (7) : 29-32. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200407011.htm
[5] 吴玮江. 天水市滑坡泥石流灾害[J]. 水文地质工程地质, 2003, (5) : 75-78. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200305017.htm
[6] 白晓华, 马金辉, 冯乐涛, 等. 基于GIS的天水市滑坡危险性评价[J]. 甘肃地质, 2008, 17(4) : 72-75. https://www.cnki.com.cn/Article/CJFDTOTAL-GSDZ200804015.htm
[7] 孟华君, 姜元俊, 张树轩, 等. 汶川地震前后都江堰山区滑坡滑动距离影响因素变化分析[J]. 地质力学学报, 2017, 23(6) : 904-913. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201706011.htm
[8] 王念秦, 张倬元, 王家鼎. 一种典型黄土滑坡的滑距预测方法[J]. 西北大学学报(自然科学版), 2003, (1) : 111-114. https://www.cnki.com.cn/Article/CJFDTOTAL-XBDZ200301030.htm
[9] 黄发明, 殷坤龙, 蒋水华, 等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 2018, 37(1) : 156-176. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801016.htm
[10] 李秀珍, 孔纪名. "5 · 12" 汶川地震诱发滑坡的滑动距离预测[J]. 四川大学学报(工程科学版), 2010, 42(5) : 243-249. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201005037.htm
[11] 刘盈, 赵方. 基于多元非线性回归和BP神经网络的长春花形态指标生长模型的比较[J]. 上海农业学报, 2019, 35(6) : 64-71. https://www.cnki.com.cn/Article/CJFDTOTAL-SHLB201906013.htm
[12] 辛大欣, 王长元, 肖峰. BP神经网络在回归分析中的应用研究[J]. 西安工业学院学报, 2002, (2) : 129-135. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGY200202007.htm
[13] 徐辉, 潘萍, 宁金魁, 等. 多元线性回归与神经网络模型在森林地上生物量遥感估测中的应用[J]. 东北林业大学学报, 2018, (1) : 63-67. https://www.cnki.com.cn/Article/CJFDTOTAL-DBLY201801012.htm
[14] 张保生, 纪昌明, 陈森林. 多元线性回归和神经网络在水库调度中的应用比较研究[J]. 中国农村水利水电, 2004, (7) : 29-32. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200407011.htm
[15] 曹朋, 郝蒙蒙, 王佳佳. 基于多元线性回归与BP神经网络的矿井瓦斯预测模型应用[J]. 煤炭技术, 2011, (11) : 91-93. https://www.cnki.com.cn/Article/CJFDTOTAL-MTJS201111040.htm
[16] 周越, 曾昭发, 唐海燕, 等. 公路勘察中滑坡体的地球物理特征与分析——以张榆线公路勘察为例[J]. 吉林大学学报(地球科学版), 2021, 51(2) : 638-644. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ202102028.htm
期刊类型引用(8)
1. 唐鹏翔，杨能，张晓美. 基于多元非线性回归和BP神经网络的矿石加工质量预测和控制. 微型电脑应用. 2025(01): 43-48 . 
百度学术
2. 林琴，郭永刚，吴升杰，臧烨祺，王国闻. 基于梯度提升的优化集成机器学习算法对滑坡易发性评价：以雅鲁藏布江与尼洋河两岸为例. 西北地质. 2024(01): 12-22 . 百度学术
3. 王本栋，李四全，许万忠，杨勇，李永云. 基于3种不同机器学习算法的滑坡易发性评价对比研究. 西北地质. 2024(01): 34-43 . 百度学术
4. 严天笑，张建通，朱月琴，刘浩然，朱浩濛. 增量学习在滑坡易发性评价中的应用——以甘肃省天水市为例. 地质通报. 2024(04): 630-640 . 本站查看
5. 周玲，郭州朋，类红磊，张延军，陈云娟. 基于BP神经网络的增强型地热系统产热性能：以伊通盆地花岗岩体热储层为例. 科学技术与工程. 2024(21): 8950-8961 . 百度学术
6. 许彬彬，张昊，李者，李光. 堤防安全的多因素预测模型及一体化管理平台探究. 水利规划与设计. 2024(11): 138-142 . 百度学术
7. 张磊，周银朋，庄宇，邢爱国，何君毅，张彦博. 贵州水城尖山营滑坡动力学特性分析与隐患点致灾范围预测. 中国地质灾害与防治学报. 2023(03): 1-7 . 百度学术
8. 吴宗琴，左双英，王露，李本云，刘晶. 层理灰岩酸性溶蚀损伤特性试验研究. 水文地质工程地质. 2023(06): 193-203 . 百度学术
其他类型引用(12)
-
图(6)
表(6)
计量
- 文章访问数: 788
- PDF下载数: 61
- 施引文献: 20