预制裂隙岩样宏细观力学行为颗粒流数值模拟

王星辰; 王志亮; 黄佑鹏; 贾帅龙

doi:10.16030/j.cnki.issn.1000-3665.202010044

预制裂隙岩样宏细观力学行为颗粒流数值模拟

合肥工业大学土木与水利工程学院，安徽合肥　230009

基金项目: 国家自然科学基金雅砻江联合基金项目（U1965101）

详细信息

作者简介: 王星辰(1996-)，男，硕士研究生，研究方向为岩石力学研究。E-mail： 269068082@qq.com

通讯作者: 王志亮(1969-)，男，博士，教授，博士生导师，主要从事岩石力学教学与科研。E-mail： cvewzL@hfut.edu.cn

中图分类号: TU458⁺.3；TU458⁺.4

收稿日期: 2020-10-23

修回日期: 2020-12-11

刊出日期: 2021-07-15

Particle flow simulation of macro- and meso-mechanical behavior of the prefabricated fractured rock sample

School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei, Anhui　230009, China

More Information

Corresponding author: WANG Zhiliang, cvewzL@hfut.edu.cn

Received Date: 23 October 2020

Revised Date: 11 December 2020

Publish Date: 15 July 2021

摘要

摘要:
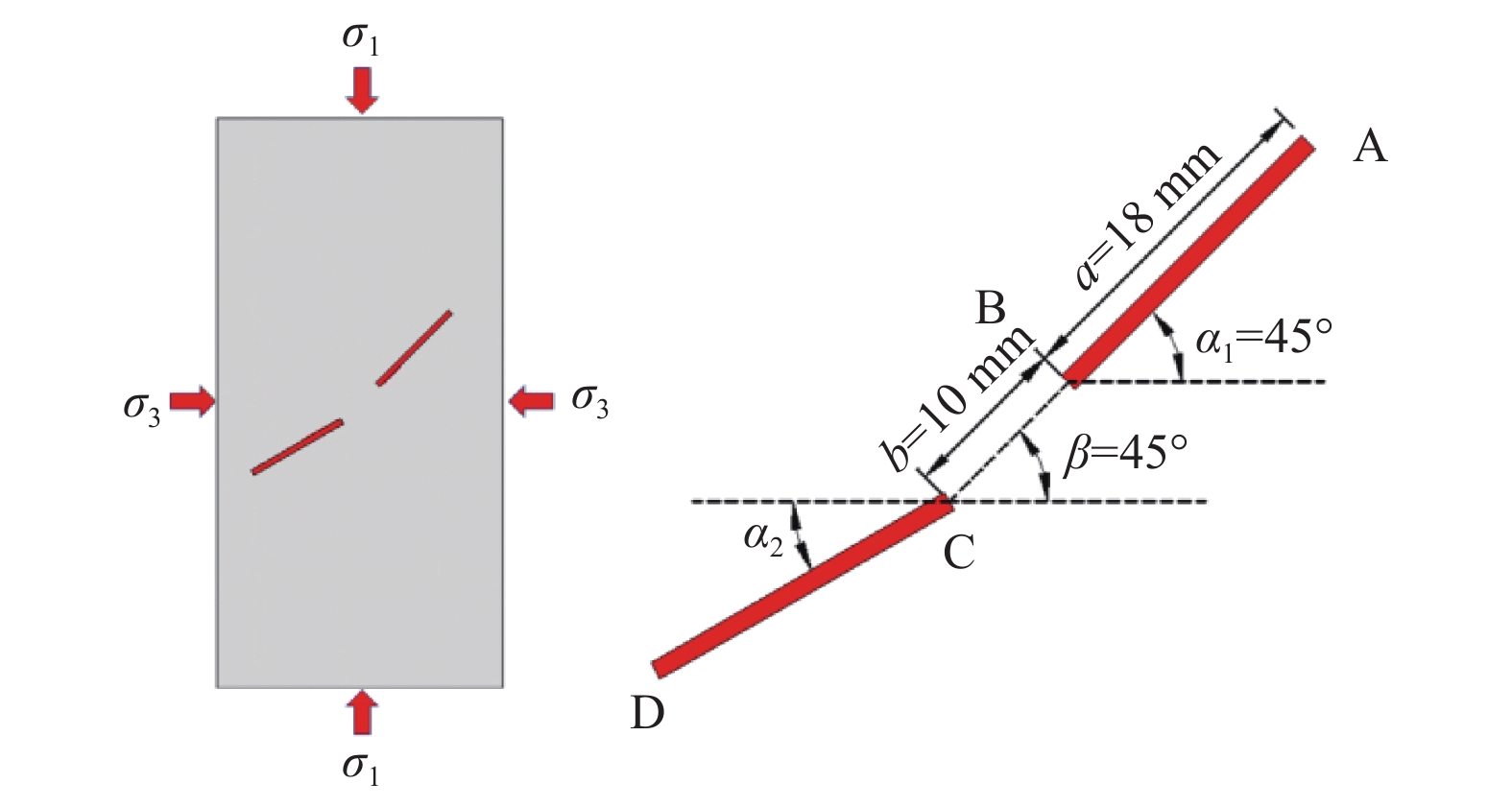
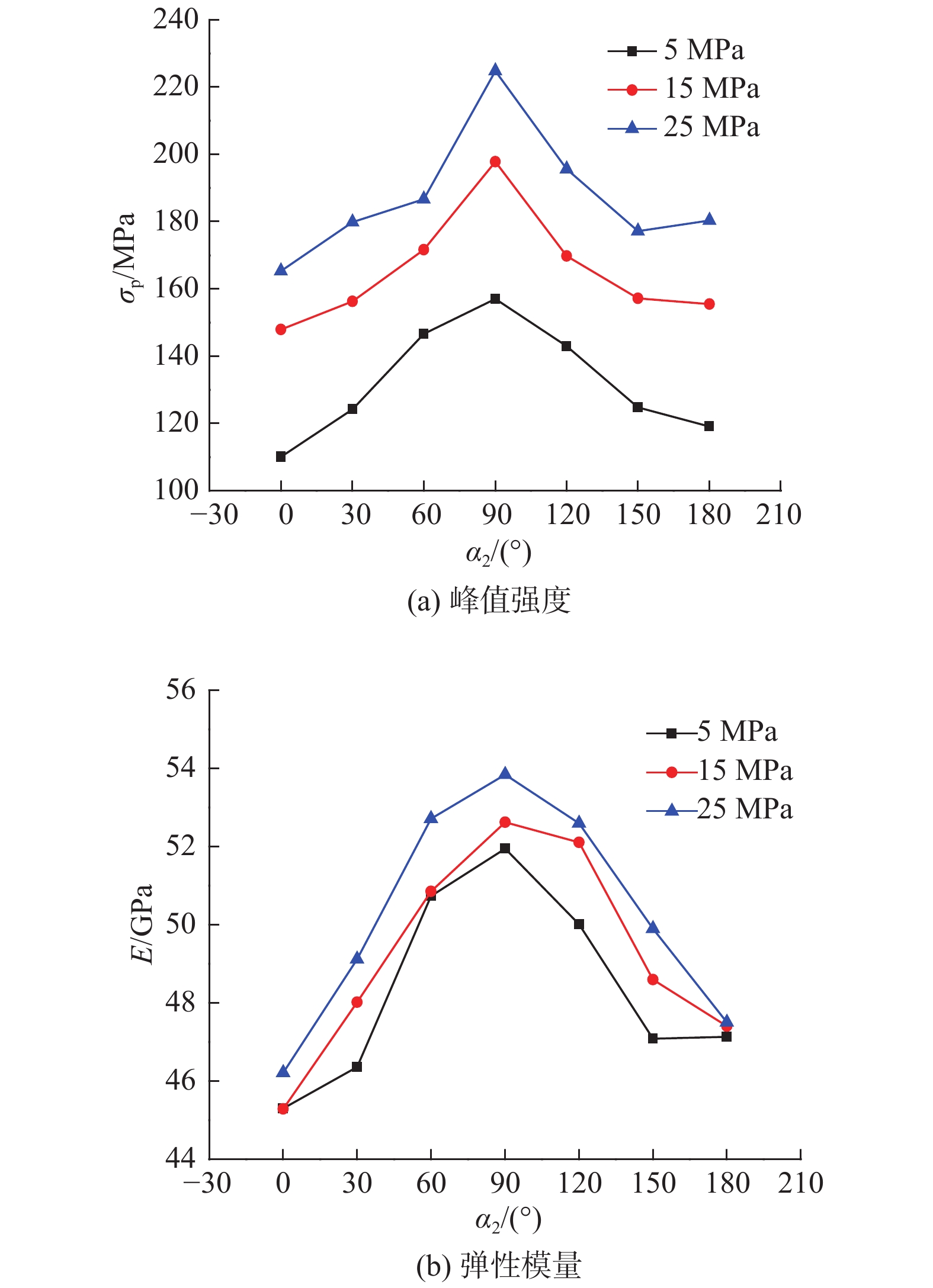
为了研究双轴压缩下预制裂隙岩样宏细观力学行为及裂纹扩展模式，采用颗粒流程序（PFC）先分析平行粘结模型细观参数对宏观参数的影响，接着结合完整花岗岩常规三轴压缩试验结果对其细观参数进行标定，最后借助该组参数模拟有围压下预制裂隙（上裂隙①和下裂隙②）岩样的力学特性。研究表明：基于PFC程序和标定的参数能较好地模拟完整岩样的破坏情况；随着围压增大，双裂隙岩样的峰值强度和弹性模量均增大，且裂隙②与水平向夹角α₂为90°时，两者均达到最大值；不同的α₂下，各岩样的裂纹演化均经过裂纹萌生、发展和稳定等3个阶段；随着围压的降低和轴向应力的增大，颗粒间的力链破坏情况愈严重。由于拉伸力链的集中和分布不同，水平裂隙长度方向上的裂纹沿着轴向扩展，且两裂隙的贯通呈现不同方式。
- 颗粒流程序 /
- 平行粘结模型 /
- 参数标定 /
- 双裂隙岩样 /
- 裂纹演化
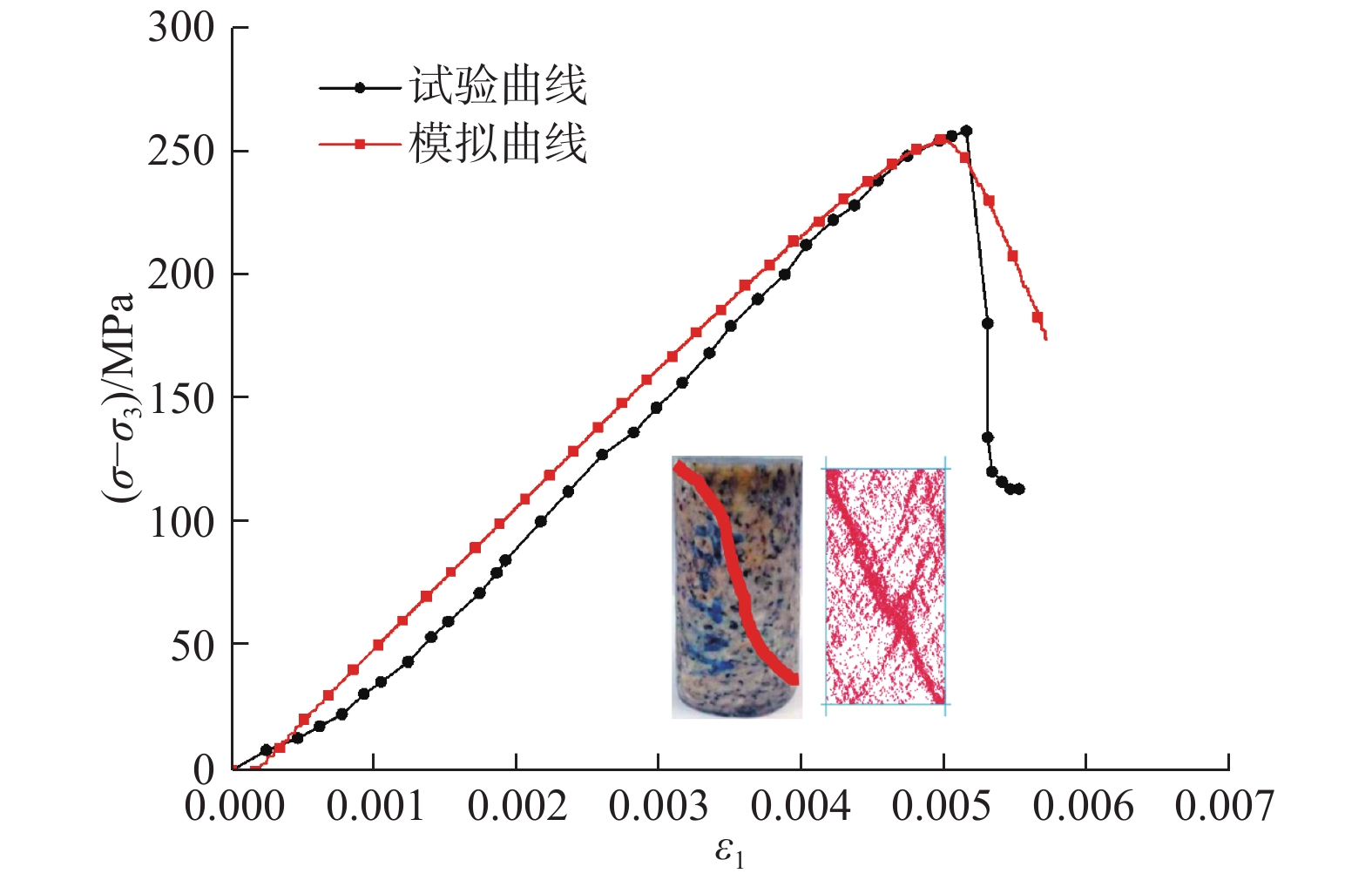
Abstract:
To examine the macro-and meso-mechanical behaviors and crack propagation mode of the prefabricated and fractured rock sample under biaxial compression, the particle flow code (PFC) is first used to study the effect of the micro-parameters of the parallel bond model on the macro-parameters. Combined with the conventional triaxial compression test of intact granite, the meso-parameters are calibrated. The mechanical properties of the sample with prefabricated double fractures (upper fracture ① and lower fracture ②) under confining pressure are simulated with the set of parameters. The results show that the PFC code and the calibrated parameters can better simulate the failure of the complete samples. As the confining pressure increases, the peak strength and elastic modulus of the double-fractured rock sample increase. When the angle α₂ between the lower fracture ② and the horizontal is 90°, both of them reach the maximum values. Under different α₂, the simulated crack evolution of each rock sample goes through three stages of crack initiation, development and stabilization. With the decreasing confining pressure and the increasing axial stress, the damage of the force chains between particles becomes more severe. Due to the difference in the concentration and distribution of the tensile force chains, the cracks along the length of the horizontal fracture propagate along the axial direction, and the penetration of the two fractures presents different ways.
- PFC /
- parallel bonding model /
- parameter calibration /
- double-fissure rock sample /
- crack evolution

HTML全文

图 1 PFC^2D模型和平行粘结键

Figure 1.

下载: 全尺寸图片幻灯片

图 2 细观参数对宏观参数的影响

Figure 2.

下载: 全尺寸图片幻灯片

图 3 试验结果与模拟结果的比较

Figure 3.

下载: 全尺寸图片幻灯片

图 4 预制双裂隙及相应的岩样模型

Figure 4.

下载: 全尺寸图片幻灯片

图 5 不同围压下裂隙角度α₂对宏观参数的影响

Figure 5.

下载: 全尺寸图片幻灯片

图 6 不同裂隙角度α₂下最终裂纹扩展形态（σ₃=5 MPa）

Figure 6.

下载: 全尺寸图片幻灯片

图 7 不同裂隙角度α₂下裂纹演化过程（σ₃=5 MPa）

Figure 7.

下载: 全尺寸图片幻灯片

图 8 α₂=0º时不同围压下岩样力链破坏情况

Figure 8.

下载: 全尺寸图片幻灯片

图 9 α₂=0°时裂隙②周围力链

Figure 9.

下载: 全尺寸图片幻灯片

图 10 围压5 MPa作用下的裂隙②周围力链

Figure 10.

下载: 全尺寸图片幻灯片

表 1 平行粘结模型参数

Table 1. Parameters of the parallel-bond model

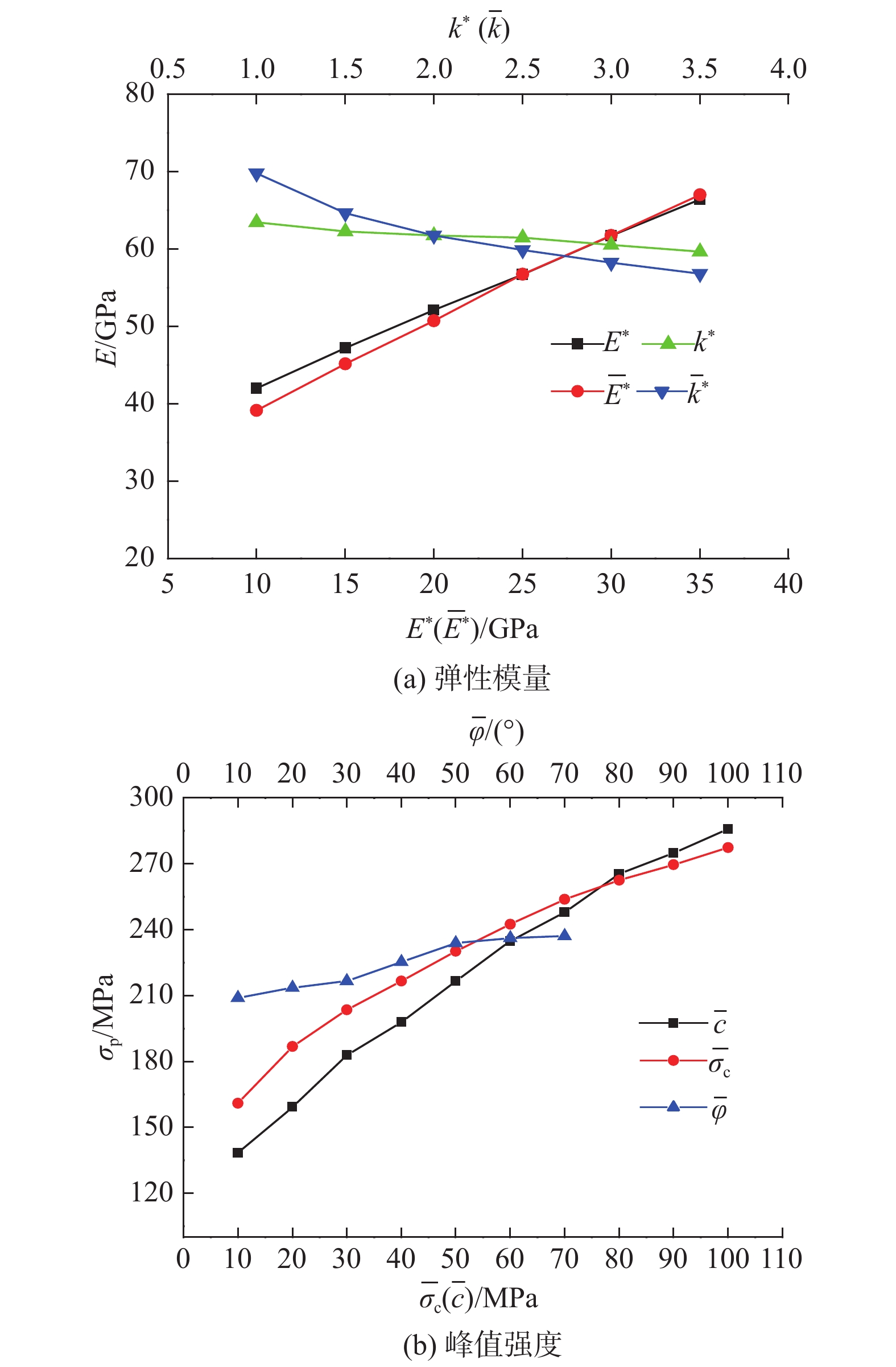
细观参数	假定值	标定值
E^*/GPa	30	41
k^*	2.0	2.6
/GPa	30	20
	2.0	2.6
/MPa	40	45
/MPa	50	85
/（°）	30	30
μ	0.70	0.56

下载: 导出CSV

参考文献(15)

[1]	罗浩, 霍宇翔, 巨能攀, 等. 弃渣场边坡的粒径分布特征及其失稳机制研究[J]. 水文地质工程地质,2020,47(1):69 − 79. [LUO Hao, HUO Yuxiang, JU Nengpan, et al. A study of the particle size distribution characteristics and instability mechanism of the slope of an abandoned slag yard[J]. Hydrogeology & Engineering Geology,2020,47(1):69 − 79. (in Chinese with English abstract)
[2]	赵国彦, 戴兵, 马驰. 平行黏结模型中细观参数对宏观特性影响研究[J]. 岩石力学与工程学报,2012,31(7):1491 − 1498. [ZHAO Guoyan, DAI Bing, Ma Chi. Study of effects of microparameters on macroproperties for parallel bonded model[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1491 − 1498. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-6915.2012.07.024
[3]	YANG S Q, HUANG Y H, JING H W, et al. Discrete element modeling on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression[J]. Engineering Geology,2014,178:28 − 48. doi: 10.1016/j.enggeo.2014.06.005
[4]	黄彦华, 杨圣奇. 非共面双裂隙红砂岩宏细观力学行为颗粒流模拟[J]. 岩石力学与工程学报,2014,33(8):1644 − 1653. [HUANG Yanhan, YANG Shengqi. Particle flow simulation of macro-and meso-mechanical behavior of red sandstone containing two pre-existing non-coplanar fissures[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(8):1644 − 1653. (in Chinese with English abstract)
[5]	王林丰. 含预制裂隙花岗岩变形破坏特征三轴试验与离散元数值分析[D]. 厦门: 华侨大学, 2017. WANG Linfeng. Analysis of deformation and failure characteristics of pre-cracked granite samples with triaxial experiments and discrete element method[D]. Xiamen: Huaqiao University, 2017. (in Chinese with English abstract)
[6]	田文岭, 杨圣奇, 黄彦华. 不同围压下共面双裂隙脆性砂岩裂纹演化特性颗粒流模拟研究[J]. 采矿与安全工程学报,2017,34(6):1207 − 1215. [TIAN Wenling, YANG Shengqi, HUANG Yanhua. PFC2D simulation on crack evolution behavior of brittle sandstone containing two coplanar fissures under different confining pressures[J]. Journal of Mining & Safety Engineering,2017,34(6):1207 − 1215. (in Chinese with English abstract)
[7]	张社荣, 孙博, 王超, 等. 双轴压缩试验下岩石裂纹扩展的离散元分析[J]. 岩石力学与工程学报,2013,32(增刊 2):3083 − 3091. [ZHANG Sherong, SUN Bo, WANG Chao, et al. Discrete element analysis of crack propagation in rocks under biaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(Sup 2):3083 − 3091. (in Chinese with English abstract)
[8]	王振永. 裂隙性围岩力学特性和破裂机理的颗粒流数值模拟研究[D]. 成都: 西南交通大学, 2016. WANG Zhenyong. Numerical simulation of mechanical properties and failure mechanism of fractured surrounding rock using particle flow code[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese with English abstract)
[9]	YAO W, CAI Y Y, YU J, et al. Experimental and numerical study on mechanical and cracking behaviors of flawed granite under triaxial compression[J]. Measurement,2019,145:573 − 582. doi: 10.1016/j.measurement.2019.03.035
[10]	何树江. 基于颗粒流的灰岩细观力学参数标定方法及其敏感性分析[D]. 济南: 山东大学, 2018. HE Shujiang. Calibration method and sensitivity analysis of micromechanic parameters for limestone based on particle flow[D]. Jinan: Shandong University, 2018. (in Chinese with English abstract)
[11]	张科, 刘享华, 杨红宣, 等. 含孔洞裂隙岩体灌浆后力学特性的物理试验与数值模拟[J]. 水文地质工程地质,2019,46(1):79 − 85. [ZHANG Ke, LIU Xianghua, YANG Hongxuan, et al. Experimental and numerical simulation of the mechanical characteristics of rocks containing hole and flaw after grouting[J]. Hydrogeology & Engineering Geology,2019,46(1):79 − 85. (in Chinese with English abstract)
[12]	SHI H, ZHANG H Q, SONG L, et al. Failure characteristics of sandstone specimens with randomly distributed pre-cracks under uniaxial compression[J]. Environmental Earth Sciences,2020,79(3):394 − 405.
[13]	HUANG Y H, YANG S Q, ZENG W. Experimental and numerical study on loading rate effects of rock-like material specimens containing two unparallel fissures[J]. Journal of Central South University,2016,23(6):1474 − 1485. doi: 10.1007/s11771-016-3200-3
[14]	刘华伟, 杨晨. 闭合与非闭合裂隙岩石单轴压缩的颗粒流细观分析[J]. 水电能源科学,2016,34(1):131 − 135. [LIU Huawei, YANG Chen. Micro-analysis of uniaxial compression of cracked rock containing open or closing fissure based on PFC[J]. Water Resources and Power,2016,34(1):131 − 135. (in Chinese with English abstract)
[15]	POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329 − 1364. doi: 10.1016/j.ijrmms.2004.09.011