Application of attenuation technology to shallow water multiples in multi-channel seismic data processing
-
摘要:
拖缆采集的海上多道地震数据受海水间传播的多次波影响，往往在共炮点道集上发育周期性的强振幅干扰波，这些噪音会掩盖海底以下及强反射层以下地层的面貌，严重影响多道地震数据的成像效果。为了消除海上多道地震数据中存在的海水间传播的多次波对地震数据的干扰，首先分析浅水多次波在海水间多次震荡的产生机制，采用了τ-P域静校正延迟技术对其进行压制，处理的核心是在τ-P域对周期性多次波模型进行预测，再通过自适应相减以去除地震数据中的多次波。实际资料处理结果表明，方法对海水间震荡的浅水多次波具有很好的压制效果，经过浅水多次波去除后的叠加剖面信噪比得到有效提高，剖面的品质得以提升。
Abstract:The multi-channel seismic data acquired by cables are often affected by multiple waves propagating between seawater and periodic strong amplitude interferences on common shot gathers, which include the seabed and the strong reflections below it. Some solutions to eliminate the interference of multiple waves are discussed in this paper. The generation mechanism of the shallow water multiple waves i.e. the multiple oscillations between sea-level and seabed are firstly discussed and analyzed. Then statics technique is used to suppress the multiples in the τ-p domain according to the vibrating characteristics of the multiples in the sea. The core of the method is to predict the cycling multiples in the τ-p domain and attenuate them by adaptive subtract. The results demonstrate that the method is effective in suppression of shallow water multiple waves caused by sea-water oscillation, the S/N ratio is obviously improved and the profile is better than that before the processing.
-
Key words:
- shallow water de-multiple /
- multi-channel seismic /
- τ-p transform
-
海底孕育了丰富的油气资源，近年来海洋油气勘探得到迅速发展，海上拖缆采集是高效的获取海洋地震资料的手段，由于海水面是一个强波阻抗界面，地震波传播到海水面产生的反极性强反射的多次波[1]是海洋地震资料处理中面临的一大难题。其压制方法可分为两大类：滤波法和预测相减法[2]。滤波法[3-4]是利用多次波与一次波的地震属性差异，选择合适的滤波方法将多次波去除；预测相减法[5-8]则通过正演或反演地震数据得到多次波模型，并由此求得多次波波场，再从原始地震记录中将其去除。
多次波主要有自由表面多次波和层间多次波[9]两种类型，自由表面多次波是指与海水表面相关的多次波，层间多次波是指在海底及海底以下地层间多次震荡产生的多次波。自由表面多次波是存在于海洋地震资料中的主要多次波类型，它在海洋地震资料上常常表现为强振幅特性，这是因为海水表面是水与空气的分界面，其反射系数近似于-1，同时由于地震波在海水中的衰减很微弱，故其振幅往往很强。所有与海水表面相关的多次波统称为自由表面多次波，目前，自由表面多次波压制方法主要包括τ-P域反褶积多次波压制方法（属于滤波法）[10-11]，高精度拉冬（radon）变换多次波压制方法（属于滤波法）[12-13]以及与此相关的技术改进算法[14-16], SRME方法（Surface-related Multiple Elimination）（属于预测相减法）[17-20]。τ-P域反褶积方法是利用多次波的周期性特征，设计相应的滤波器将周期出现的成分压制[21]，该方法假设多次波需具有良好的周期性，对于短周期多次波的压制比较有效；高精度拉冬变换[11-13]是利用多次波与一次波的速度差异实现多次波与一次波的分离，首先将地震数据进行正常时差校正再变换到拉冬域，利用多次波与一次波在拉冬域的可分离性压制多次波组分，再将结果变换回时空域，该方法在消除中远偏移距多次波方面效果明显；SRME方法[22-23]为数据驱动的多次波预测方法，以地震数据本身作为预测算子，不需要已知地下介质的先验信息，并且可以同时预测出所有的自由表面多次波，该方法在深水区域去除多次波效果显著，但由于其需要在原始地震记录中减去多次波信息，易损害信噪比较低数据中的有效信号。稀疏反演一次波估计方法（Estimation of Primaries by Sparse Inversion, EPSI）无需对预测的多次波与原始数据进行匹配相减，即可同时重构一次波与多次波[24]，避免了匹配相减对一次波的伤害，目前由于该方法计算成本限制，无法对实测数据进行工业应用[9]。但是目前并不存在一种方法能够完全一次性消除多次波，多次波的去除需要多种技术方法配合使用，通过多步去除最终达到消除多次波的目的。
中国近海大陆架面积广阔，这些区域大多水深较浅，多道地震数据中往往存在较严重的浅水多次波干扰问题。浅水多次波降低了地震剖面的信噪比，掩盖了真实构造层位的空间展布。本文针对近海陆架浅水区地震资料，通过分析浅水区域多次波的特点，认为在海平面和海底面之间震荡的多次波对浅水区地震资料品质影响最大。因此，文章聚焦浅水区水层中震荡多次波的特点，研制对应的多次波压制手段：首先研究了浅水多次波的预测方法，并采用τ-P域的静校正延迟技术预测多次波模型，再通过自适应相减从原始数据中减去多次波以实现多次波的压制。中国近海某多道地震测线实际资料处理结果表明，本文方法在去除浅水多次波方面具有显著的效果，为近海浅水地震资料的多次波压制提供了良好的技术手段。
1. 浅水多次波的特点
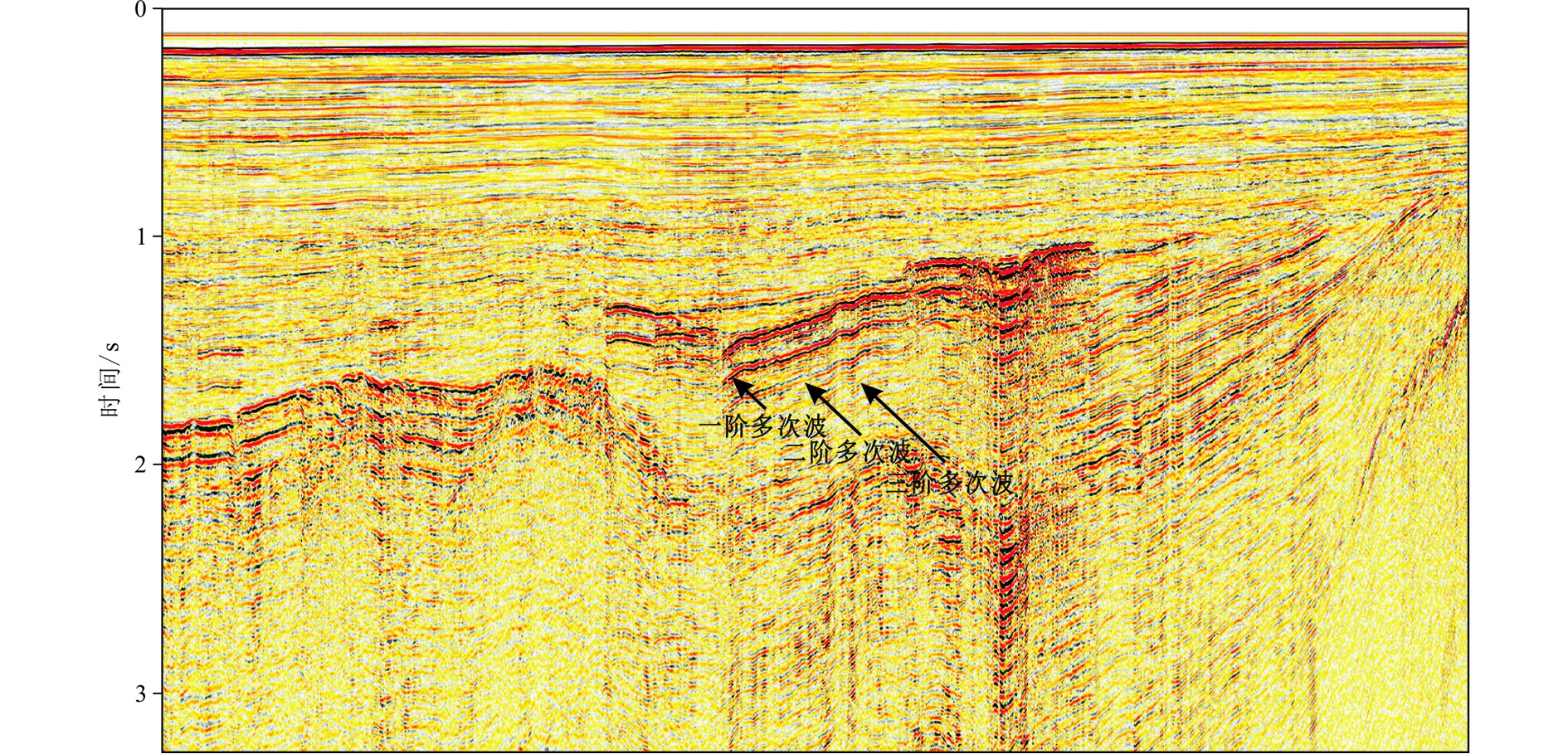
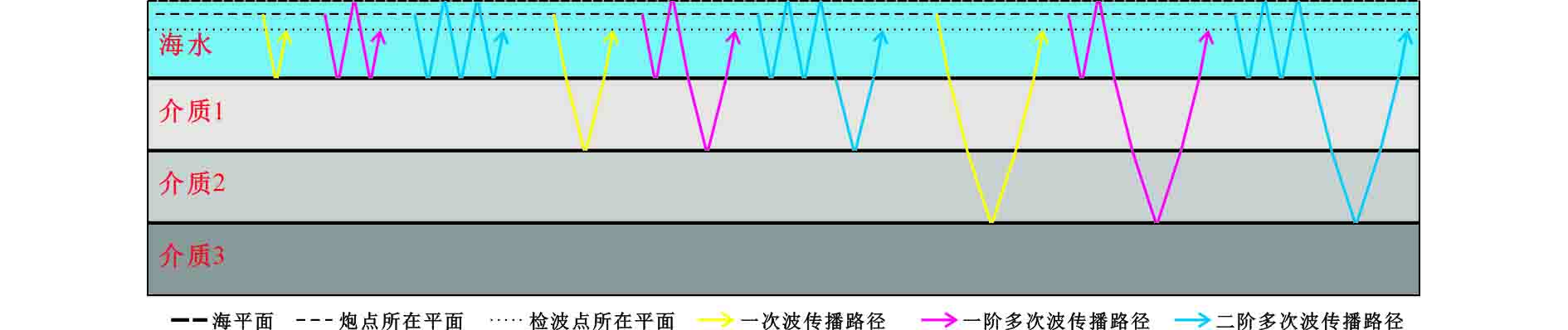
浅水多次波的特点是由于海水较浅，有效波在海水层中多次震荡，并且水层对地震波能量衰减较小，造成有效波与多次波难以区分。图1给出了该类型浅水多次波的传播路径，在零偏移距条件下，多次波的周期为海平面到海底的双程旅行时。多次波的识别既可在炮集上进行也可在共偏移距道集上进行，由于共偏移距道集相对炮集更容易识别出地质构造，可靠性更高，因此，一般更倾向于在共偏移距道集上对多次波情况进行评估。近偏移距道集可以近似看作自激自收剖面，在层位上较容易识别出多次波（图2中的黑色箭头所指），由图可见多次波紧跟有效波，呈现出周期性特点，这种效应是由多次波在海水中反复传播引起的。
图 1. 浅水多次波传播路径示意图Figure 1. Schematic diagram of multiple propagation paths in shallow water通过分析浅水多次波的特点，发现以下规律：① 多次波在道集上表现出周期性特点，且这种周期性与海水深度有关，海水越深多次波出现的时间越晚；② 紧跟有效层位的多次波往往比较明显，即一阶多次波在成像剖面中比较明显，二阶以上多次波能量明显减弱，此种现象在海上多道地震数据中普遍存在。因此，根据以上基本假设条件，设计相应的处理流程来解决这种类型多次波的压制问题。
2. 浅水多次波衰减原理
根据上文的分析，对于浅水地震资料，海水中震荡的多次波对成像效果影响最大，因此，本文主要研究在海水间震荡的多次波压制方法。基本思路为先预测出多次波模型，再从数据中将多次波减去，问题的关键是寻找一种适合浅水特点的多次波模型预测方法。
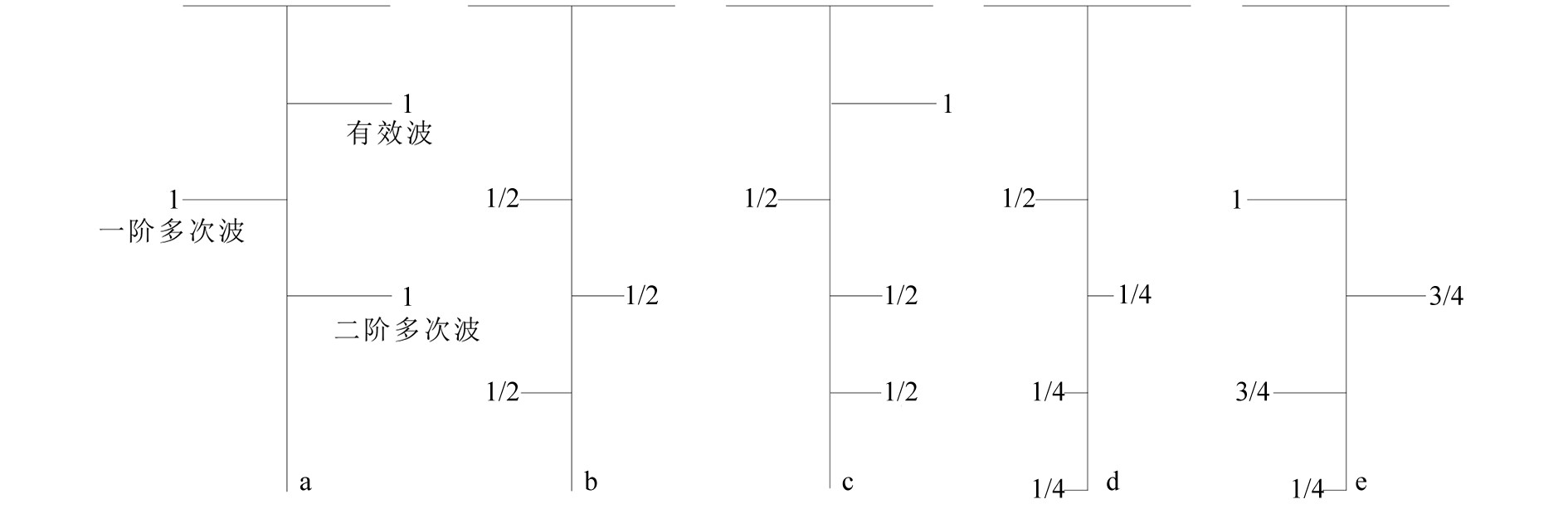
海上拖缆采集条件下，炮点和接收点一般放置于海水面以下，为简化问题，忽略海底以下反射信息，仅分析海底的一次反射波与多次波特点。零偏移距条件下，浅水多次波模型的预测过程如图3所示。图3a展示了地震波在海水模型中传播得到的有效波和多次波的脉冲振幅与极性，不考虑海水的吸收衰减，那么假设一次有效波的振幅为1，一阶多次波经历一次海水面反射，假设其振幅为−1，二阶多次波经历两次海水面反射，假设其振幅为1。多次波出现的周期T为海平面到海底的双程旅行时。
海水多次波的预测可以通过4步实现：① 将含有多次波的数据（图3a）做T时间延迟，再将振幅值乘以−0.5，得到图3b；② 将图3a减去图3b得到图3c；③ 再将图3c做T时间延迟，并将振幅乘以−0.5，得到图3d；④ 将图3b和图3d相加得到图3e。由图3e可见，经过以上4步，可以完全将一阶多次波预测出来，并能够预测出二阶多次波及多阶多次波的大部分能量。这样做的目的是防止由于多次波周期T计算不准时，误差累加会导致预测的多阶多次波时间与真实时间之间出现较大差距，有利于有效信号的保护。
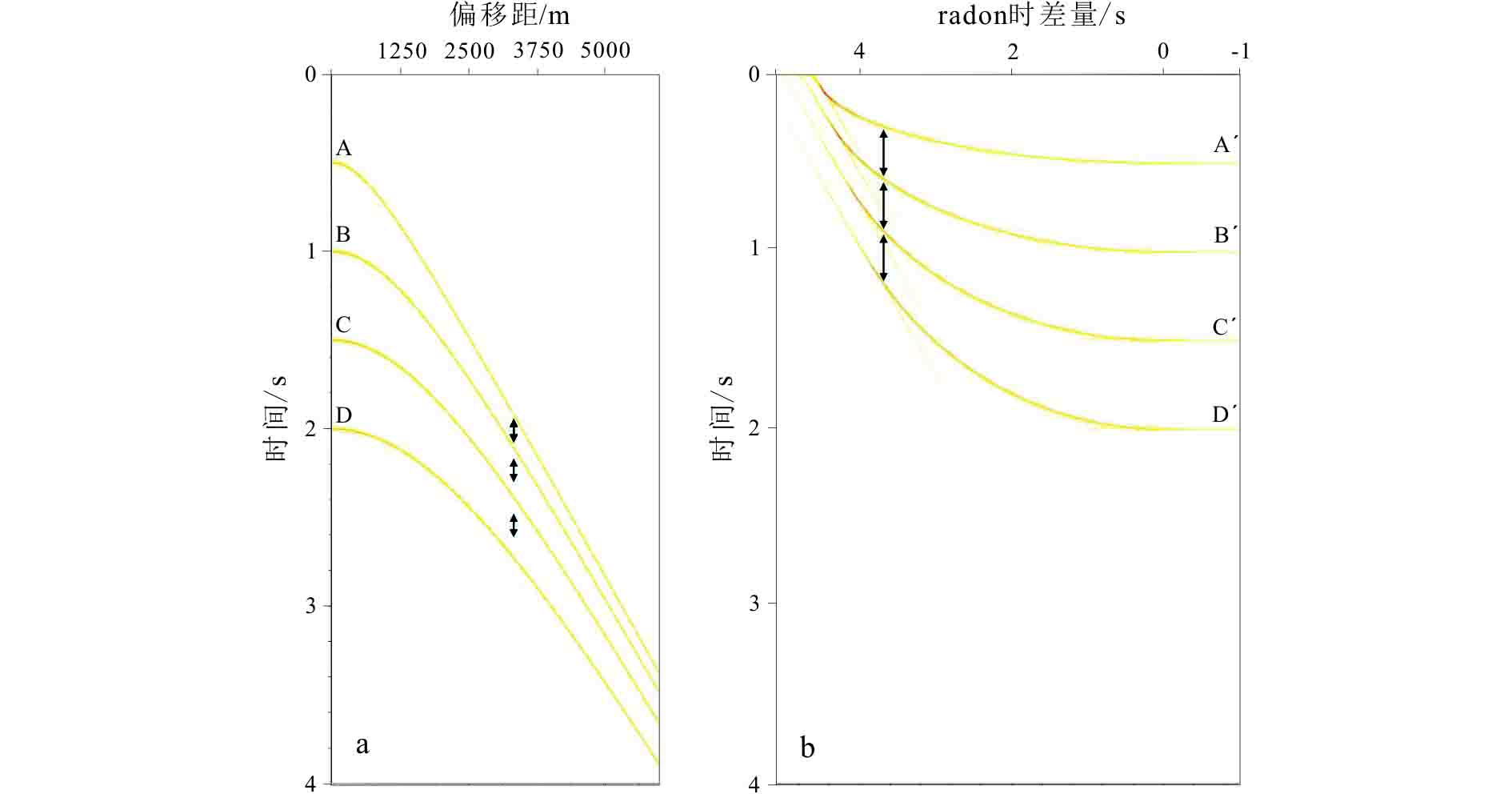
以上分析基于零偏移距假设，在非零偏移距条件下，由于双曲效应，时空域中多次波不再保持等时差出现。图4a给出了浅水多次波在时空t-x域和τ-P域中的特点，由图可见，在t-x域中（图4a）近偏移距时多次波近似满足周期性出现的特点，但是在远偏移距处，多次波的出现时间不符合等时差规律。图4b是将炮集数据从时空域通过线性拉冬变换转换到τ-P域，由图可见，在不同的radon时差量处，多次波均表现出良好的周期性。因此，在τ-P域中利用多次波的周期性出现特征可以实现浅水多次波的准确预测。
3. 浅水多次波衰减的关键技术
通过对浅水多次波衰减原理的分析可知，浅水多次波去除方法的流程较长（图5），涉及到的浅水多次波的周期计算、自适应相减等都会影响多次波的压制效果，因此,有必要对关键参数的选择进行分析和研究，通过实际处理效果确定最佳参数组合。
3.1 浅水多次波在τ-P域周期的计算
在τ-P域，浅水多次波具有周期性，其周期可以用下面的公式计算：
$ T = t\sqrt {1 - {{\left( {pv} \right)}^2}} $ (1) 其中，t为海底的反射时间，p为慢度，v为海水的速度。在实际处理时，一般更习惯使用radon时差量来表示慢度，表示为：
$ p = \frac{r}{x} $ (2) 其中，r为radon时差量，x为参考偏移距，一般设为最大偏移距。radon时差量决定了τ-P变换数据范围，通过最大时差和最小时差控制，最大时差为正值，方向向下，最大值一般以海水速度为依据，即
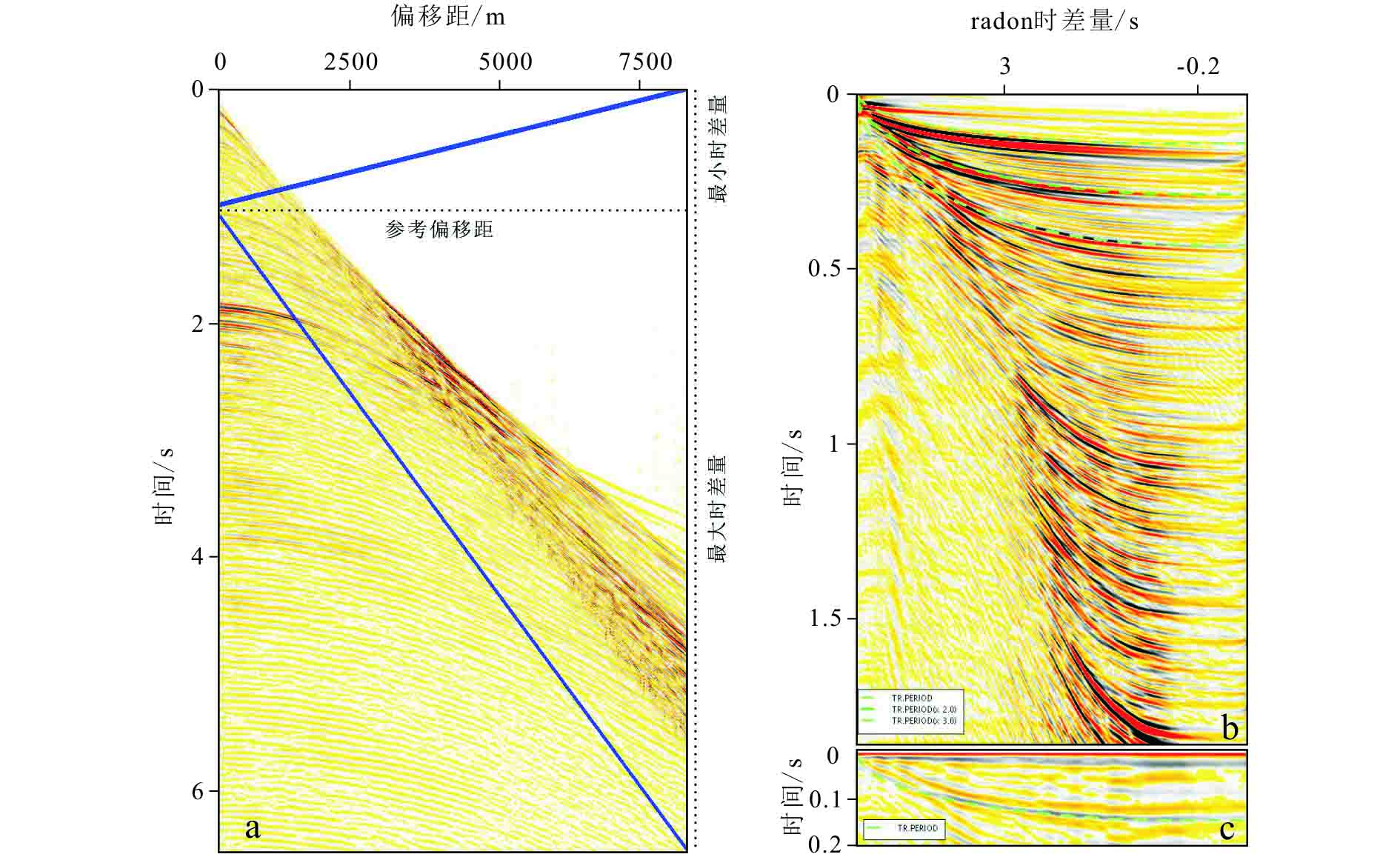
$ {\rm{max}}\_r = \frac{{{\rm{offset}}}}{v} $ (3) 其中，max_r为最大时差量，offset为参考偏移距，v为海水速度，一般设为1 500 m/s。在浅水区域，有效波基本上都是向下倾斜，很少存在向上绕射的有效波，因此，最小时差量的设置仅是为减少τ-P变换过程中的能量损失，一般设置为最大时差量的四分之一左右。参考偏移距、最小时差量和最大时差量的设置可见图6a。
图 6. τ-P变换和浅水多次波周期计算a. 炮集，b. τ-P域结果，c. 自相关。Figure 6. The τ-P transform and the period of shallow water multiplesa. τ-P transform of the shot gather， b. τ-P domain result， c. the autocorrelation.图6b为图6a将蓝线区域内的数据变换到τ-P域的结果，可以看到浅水多次波在τ-P域上具有明显的周期性，其时差与计算的周期T吻合较好，对其做自相关可以发现浅水多次波周期T在自相关图中也可以较好吻合（图6c），表明浅水多次波符合在海水之间震荡的特点，这是本文方法压制浅水多次波的基础。实际上，对于本文的方法，多次波去除效果的好坏关键在于多次波模型预测的效果，对于多次波的预测关键在于其计算周期与实际资料能否很好地匹配，因此，通过τ-P域的自相关验证计算周期T与实际资料的符合程度是关键的质控手段。
3.2 自适应相减
得到多次波模型后，需要通过自适应相减将多次波进行压制，这是浅水多次波压制的最后一步。自适应相减的实现是依据一定的规律将数据集在时间和空间上划分为多个重叠的窗口，在每个窗口中计算出地震数据与多次波模型的最佳匹配滤波器，再从地震数据中将滤波后的多次波模型减去。
自适应相减有一维滤波（仅时间）和二维滤波（包含时间和空间）两种算法，一维滤波仅对每一地震道在时间上进行匹配滤波，而二维滤波不但考虑每一地震道在时间上的匹配，同时考虑它与相邻地震道在空间上的匹配，所以理论上二维滤波效果好于一维滤波，但需要更大的计算内存与计算时间。在海底较平、构造简单，或多次波模型比较准确的条件下，两者计算结果差别不大，此时综合考虑计算效果与计算效率，往往采用一维滤波算法。
此外，自适应相减可在炮域或道域中实现，炮域道集即常规的共炮点道集，道域道集为共偏移距道集。一般而言，自适应相减在共偏移距道域中实现效果更好，这是因为在共偏移距道域中，偏移距相同或相差不大，地质构造的影响在一个共偏移距道域剖面上被平均化；同时，近道（小偏移距）数据往往是由小角度入射的地震波组成的，而大偏移距数据往往包含更多大角度入射波信息，因此可以解决在炮记录中的各道记录由于方向性效应的影响，震源信号会随着传播角度的不同而有所差异的问题。
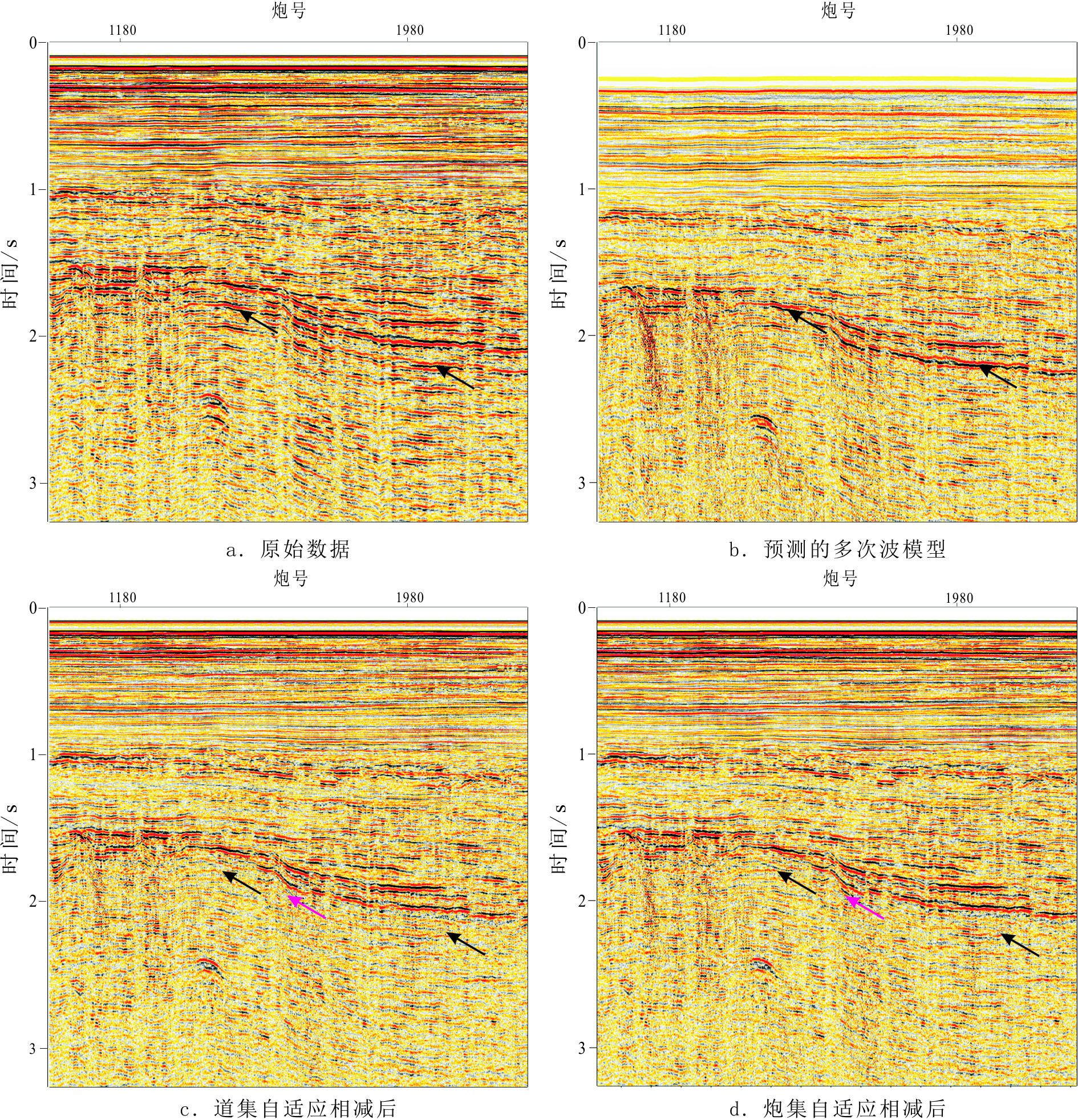
根据对自适应相减的分析，经过实验，在实际资料处理中采用表1所示的参数。自适应相减的结果见图7，由图可见，黑色箭头指示一阶多次波，可以看到多次波模型预测较准确，在自适应相减后多次波得到明显压制；对比图7c和图7d，可见图中粉色箭头指示处在炮集中进行自适应相减会有多次波的残留，在共偏移距道集中进行自适应相减可以实现多次波的最大化去除。图8对比了本文方法与SRME方法压制浅水多次波的效果，由图可见，SRME方法可以压制长周期的多次波，但对在海水间震荡的多次波去除效果不足，黑色箭头处存在较多的多次波残留。
表 1. 自适应相减所采用的参数Table 1. The parameters of adaptive subtract参数 参数值 自适应相减类型 最小平方1D算法 计算域 道域 时间窗口长度 500 ms 空间窗口长度 50 滤波长度 11 | Show Table
DownLoad:
CSV
3.3 实际资料效果分析
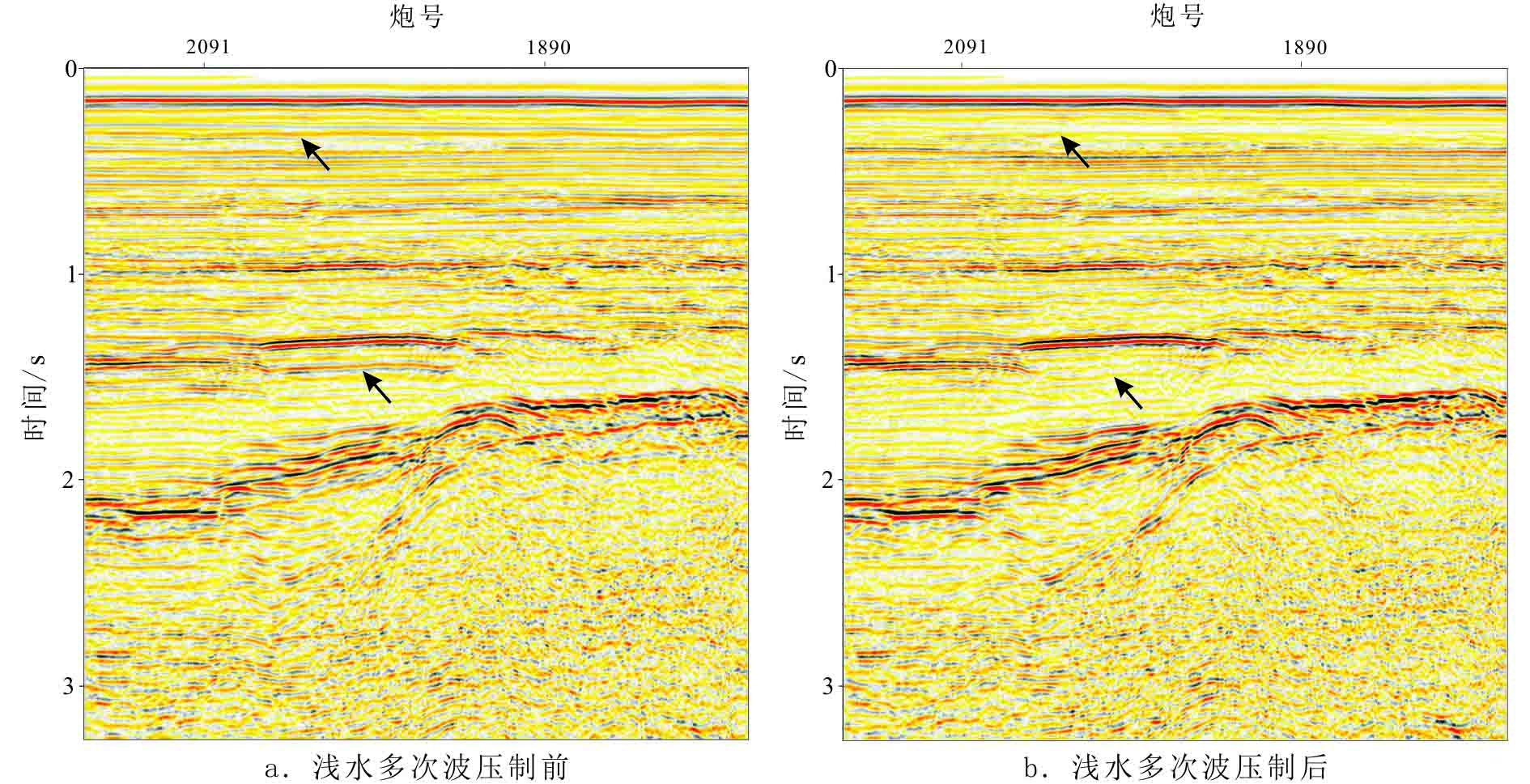
通过实际处理时参数的调整和实验，图9展示了本文方法压制浅水多次波前后的叠加剖面。由图可见，影响该区的多次波主要是一阶自由表面多次波，经过浅水多次波压制后，海底的一阶多次波和海底下强反射界面的一阶多次波得到有效衰减，有利于层位的识别与追踪；由于海底面的一阶多次波具有很强的能量，压制前海底下层位较多，各层能量级别相似，压制后有效波得到凸显，波组特征更加明显，信噪比得到提高。
4. 结论
（1）大陆架浅水平缓海底地区浅水多次波的特点表现为：在海水间传播的多次波最为发育，其中该类多次波中的一阶多次波对地震资料影响最为明显。
（2）τ-P域静校正延迟方法可以实现多次波的准确预测，通过自适应相减可以对其进行有效压制。
（3）在τ-P域，计算的多次波周期应该与实际资料相吻合，通过自相关道集进行质控是多次波模型预测准确与否的关键。
（4）浅水多次波压制技术是根据实际资料的特点研究的一种组合算法，主要适用于海底平缓的浅水地区，中国渤海、黄海和东海大陆架的大多数海区都符合这一条件,本文算法对这些地区的地震资料处理均具适用性。
致谢：感谢青岛海洋地质研究所东海油气调查项目提供地震数据支持。
-
表 1 自适应相减所采用的参数
Table 1. The parameters of adaptive subtract
参数 参数值 自适应相减类型 最小平方1D算法 计算域 道域 时间窗口长度 500 ms 空间窗口长度 50 滤波长度 11
下载: 导出CSV
-
[1] Dragoset B. A practical approach to surface multiple attenuation [J]. The Leading Edge, 1999, 18(1): 104-108. doi: 10.1190/1.1438132
[2] Weglein A B. Multiple attenuation: an overview of recent advances and the road ahead [J]. The Leading Edge, 1999, 18(1): 40-44. doi: 10.1190/1.1438150
[3] Robinson E A. Predictive decomposition of seismic traces [J]. Geophysics, 1957, 22(4): 767-778. doi: 10.1190/1.1438415
[4] Taner M T. Long period sea-floor multiples and their suppression [J]. Geophysical Prospecting, 1980, 28(1): 30-48. doi: 10.1111/j.1365-2478.1980.tb01209.x
[5] Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part I: theoretical considerations [J]. Geophysics, 1997, 62(5): 1586-1595. doi: 10.1190/1.1444261
[6] Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data [J]. Geophysics, 1997, 62(6): 1975-1989. doi: 10.1190/1.1444298
[7] Ypma F H C, Verschuur D J. Estimating primaries by sparse inversion, a generalized approach [J]. Geophysical Prospecting, 2013, 61(S1): 94-108.
[8] 白兰淑, 刘伊克, 卢回忆. 稀疏反演多次波去除策略与效果分析[J]. 地球物理学报, 2017, 60(12):4801-4813 doi: 10.6038/cjg20171221
BAI Lanshu, LIU Yike, LU Huiyi. Strategy of multiple elimination by sparsity inversion and its effectiveness analysis [J]. Chinese Journal of Geophysics, 2017, 60(12): 4801-4813. doi: 10.6038/cjg20171221
[9] Verschuur D J. Seismic Multiple Removal Techniques: Past, Present and Future[M]. Houten, Netherlands: EAGE Publications, 2006.
[10] Stoffa P L, Buhl P, Diebold J B, et al. Direct mapping of seismic data to the domain of intercept time and ray parameter – a plane-wave decomposition [J]. Geophysics, 1981, 46(3): 255-267. doi: 10.1190/1.1441197
[11] Hampson D. Inverse velocity stacking for multiple elimination [J]. Journal of the Canadian Society of Exploration Geophysicists, 1986, 22(1): 44-55.
[12] 贾连凯, 吴时国, 赵昌垒. 多次波压制技术在南海北部陆缘深水区的应用[J]. 地球物理学进展, 2014, 29(2):920-930 doi: 10.6038/pg20140260
JIA Liankai, WU Shiguo, ZHAO Changlei. Application of multiple elimination techniques in the deepwater continental margin of northern South China Sea [J]. Progress in Geophysics, 2014, 29(2): 920-930. doi: 10.6038/pg20140260
[13] 刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1):8-15 doi: 10.3969/j.issn.1004-2903.2004.01.002
LIU Xiwu, LIU Hong, LI Youming. High resolution radon transform and its application in seismic signal processing [J]. Progress in Geophysics, 2004, 19(1): 8-15. doi: 10.3969/j.issn.1004-2903.2004.01.002
[14] 牛滨华, 孙春岩, 张中杰, 等. 多项式Radon变换[J]. 地球物理学报, 2001, 44(2):263-271 doi: 10.3321/j.issn:0001-5733.2001.02.014
NIU Binhua, SUN Chunyan, ZHANG Zhongjie, et al. Polynomial radon transform [J]. Chinese Journal of Geophysics, 2001, 44(2): 263-271. doi: 10.3321/j.issn:0001-5733.2001.02.014
[15] 熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 2009, 52(4):1068-1077 doi: 10.3969/j.issn.0001-5733.2009.04.024
XIONG Deng, ZHAO Wei, ZHANG Jianfeng. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple [J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077. doi: 10.3969/j.issn.0001-5733.2009.04.024
[16] 石颖, 王维红. 基于波动方程预测和双曲Radon变换联合压制表面多次波[J]. 地球物理学报, 2012, 55(9):3115-3125 doi: 10.6038/j.issn.0001-5733.2012.09.029
SHI Ying, WANG Weihong. Surface-related multiple suppression approach by combining wave equation prediction and hyperbolic Radon transform [J]. Chinese Journal of Geophysics, 2012, 55(9): 3115-3125. doi: 10.6038/j.issn.0001-5733.2012.09.029
[17] Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive surface-related multiple elimination [J]. Geophysics, 1992, 57(9): 1166-1177. doi: 10.1190/1.1443330
[18] Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, Part II: practical aspects and examples [J]. Geophysics, 1997, 62(5): 1596-1611. doi: 10.1190/1.1444262
[19] 肖二莲, 陈瑜, 万欢, 等. SRME多次波衰减方法在海洋地震资料中的应用[J]. 地球物理学进展, 2010, 25(3):1057-1064 doi: 10.3969/j.issn.1004-2903.2010.03.046
XIAO Erlian, CHEN Yu, WAN Huan, et al. Surface-related multiple elimination on marine seismic data [J]. Progress in Geophysics, 2010, 25(3): 1057-1064. doi: 10.3969/j.issn.1004-2903.2010.03.046
[20] 马继涛, Mrinal S K, 陈小宏, 等. 海底电缆多次波压制方法研究[J]. 地球物理学报, 2011, 54(11):2960-2966 doi: 10.3969/j.issn.0001-5733.2011.11.026
MA Jitao, Mrinal S K, CHEN Xiaohong, et al. OBC multiple attenuation technique using SRME theory [J]. Chinese Journal of Geophysics, 2011, 54(11): 2960-2966. doi: 10.3969/j.issn.0001-5733.2011.11.026
[21] Robinson E A. Predictive decomposition of time series with applications to seismic exploration[D]. Doctor Dissertation of MIT, 1954.
[22] Berkhout A J. Seismic Migration: Imaging of Acoustic Energy by Wave Field Extrapolation A: Theoretical Aspects[M]. 2nd ed. Amsterdam: Elsevier, 1982.
[23] Verschuur D J. Surface-related multiple elimination, an inversion approach[D]. Doctor Dissertation of Delft University of Technology, 1991.
[24] van Groenestijn G J A, Verschuur D J. Estimating primaries by sparse inversion and application to near-offset data reconstruction [J]. Geophysics, 2009, 74(3): A23-A28. doi: 10.1190/1.3111115
期刊类型引用(9)
1. 刘鸿，徐华宁，刘欣欣，陈江欣，张菲菲，王小杰，颜中辉，杨佳佳，杨睿. 海洋地球物理数据处理现状及展望. 海洋地质与第四纪地质. 2024(03): 40-52 . 
本站查看
2. 王小杰，刘欣欣，颜中辉，刘鸿，杨佳佳. 基于曲波域模型优化的多次波压制方法在浅地层剖面的应用. 石油物探. 2024(06): 1155-1162 . 百度学术
3. 周东红，段新意. 浅水环境下气云发育区高孔低胶结地层地震资料成像策略研究——以渤海莱北地区A油田为例. 石油物探. 2023(01): 105-118 . 百度学术
4. 邢子浩，蔡砥柱，张林，陈靓，孟庆杰，王瑞，李奇，陈治国，鲁旭. 基于整形正则化非平稳回归技术的匹配滤波压制单道地震鬼波方法及应用. 地球物理学进展. 2023(01): 502-512 . 百度学术
5. 龙成，孙辉，安永宁. 海上风电场址浅地层剖面信息采集及关键处理技术. 水道港口. 2023(03): 473-479 . 百度学术
6. 易虎，詹文欢，闵伟，吴晓川，李健，冯英辞，任治坤. 小多道地震震源效果在海域活动断裂探测中的对比研究. 地震地质. 2022(02): 333-348 . 百度学术
7. 邢子浩，陈靓，杨德鹏，杨册，翟继锋，周大森，王明，韦成龙. 基于正则化非平稳回归技术的自适应匹配相减在单道地震多次波压制中的应用. 海洋地质前沿. 2021(02): 70-76 . 百度学术
8. 王小杰，颜中辉，刘俊，刘欣欣，杨佳佳. 基于模型优化的广义自由表面多次波压制技术在印度洋深水海域的应用. 海洋地质与第四纪地质. 2021(05): 221-230 . 本站查看
9. 颜中辉，王小杰，刘媛媛，徐华宁，杨佳佳，杨长清，杨传胜. 东海多次波压制的关键技术. 海洋地质前沿. 2020(07): 64-72 . 百度学术
其他类型引用(3)
-
图(9)
表(1)
计量
- 文章访问数: 2710
- PDF下载数: 337
- 施引文献: 12