INSTABILITY MODEL OF VERTICAL LAYER ROCK SLOPE BASED ON THE STATISTICAL CONSTITUTIVE DAMAGE MODEL
-
摘要:
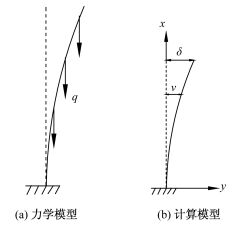
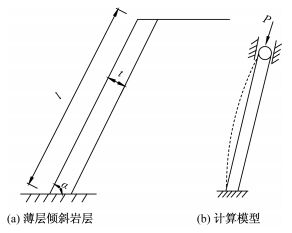
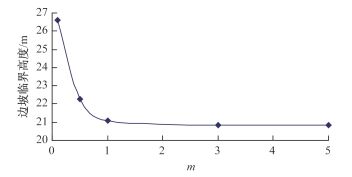
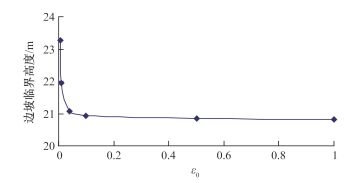
根据直立层状岩石边坡的实际失稳模式,基于欧拉压杆失稳模型建立了直立层状岩石边坡在自重荷载作用下的失稳计算模型及临界高度计算方法。同时基于岩石内部含有初始损伤的客观事实,建立了基于统计损伤模型的直立层状岩石边坡失稳模型,并对两种不同模型的计算结果进行了讨论。研究结果表明,根据自重荷载作用下的失稳计算模型计算得到的直立岩质边坡溃屈失稳破坏临界高度约为其他研究者相应计算结果的75%,更符合边坡的实际受力特征及破坏情况。基于岩石统计损伤本构模型提出的直立层状岩石边坡失稳模型不但考虑了岩石的弹性模量等参数,而且结合了应力-应变曲线等特征,得出的结果也更符合实际。研究还发现计算参数m、ε0的变化对计算结果有较大影响,说明在类似问题中考虑岩石的损伤演化特性十分必要。
Abstract:According to the actual instability mode of the vertical layer rock slope, the instability calculation model and critical height calculation method under self-gravity load for the vertical layer rock slope on the basis of the Euler pressure bar instability failure method are established. Meanwhile, based on the fact that rock has initial damage, the instability model of the vertical layer rock slope based on the statistical damage model is set up, and the calculation results based on the two models above are discussed. The study result shows that the critical height of the vertical layer rock slope calculated by the method proposed in this paper is about 75% that of other researchers, which is more suitable for the actual loading characteristic and failure condition. The instability model of the vertical layer rock slope based on the rock statistical damage constitutive model not only considers the rock mechanical parameters such as elastic modulus, but also combines the characteristic of the stress-strain curve, from which the calculation result is more suitable for the actual condition. It is also found that the change of the calculation parameters m andε0 has much effect on the calculation results, which indicates that it is very necessary to consider rock damage evolution in the similar problem.
-

-
[1] Cavers D S. Simple methods to analyze bulking of rock slopes[J]. Rock Mechanics, 1981, 14(2):87~104. doi: 10.1007/BF01239857
[2] 孙广忠, 孙毅.岩体力学原理[M].北京:科学出版社, 2011.
SUN Guang-zhong, SUN Yi. Principle of rock mass mechanics[M]. Beijing:Science Press, 2011.
[3] 孙强, 朱术云, 薛雷, 等.力矩效应对顺层岩质边坡稳定性的影响[J].煤炭学报, 2011, 33(5):762~765. http://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201105011.htm
SUN Qiang, ZHU Shu-yun, XUE Lei, et al. The instability analysis of bedding rock slope based on moment of force[J]. Journal of China Coal Society, 2011, 33(5):762~765. http://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201105011.htm
[4] 林杭, 曹平, 李江腾, 等.层状岩质边坡破坏模式及稳定性的数值分析[J].岩土力学, 2010, 31(10):3300~3304. doi: 10.3969/j.issn.1000-7598.2010.10.043
LIN Hang, CAO Ping, LI Jiang-teng, et al. Numerical analysis of failure modes and stability of stratified rock slopes[J]. Rock and Soil Mechanics, 2010, 31(10):3300~3304. doi: 10.3969/j.issn.1000-7598.2010.10.043
[5] 郭彬彬, 赵卫华, 王红才, 等.千灵山岩质边坡地质雷达探测及稳定性分析[J].地质力学学报, 2013, 19(1):104~112. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20130111&journal_id=dzlxxb
GUO Bin-bin, ZHAO Wei-hua, WANG Hong-cai, et al. Geological radar survey and stability analysis of rock slope in Qianling Mountain based on strength reduction FEM[J]. Journal of Geomechanics, 2013, 19(1):104~112. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20130111&journal_id=dzlxxb
[6] 杜宇本, 郑光, 蒋良文, 等.大瑞铁路澜沧江大桥工程边坡稳定性三维数值模拟分析[J].地质力学学报, 2010, 16(1):108~114. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20100113&journal_id=dzlxxb
DU Yu-ben, ZHENG Guang, JIANG Liang-wen, et al. 3D numerical simulation of slope stability of Lancangjiang Bridge on Dali-Ruili Railway[J]. Journal of Geomechanics, 2010, 16(1):108~114. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20100113&journal_id=dzlxxb
[7] 陈晓洋, 张宏阳, 冀东, 等.重庆某不稳定斜坡变形监测及稳定性分析[J].地质力学学报, 2011, 17(4):402~409. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20110410&journal_id=dzlxxb
CHEN Xiao-yang, ZHANG Hong-yang, JI Dong, et al. Deformation monitoring and stability analysis of an unstable slope in Chongqing City[J]. Journal of Geomechanics, 2011, 17(4):402~409. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20110410&journal_id=dzlxxb
[8] 张天军, 李云鹏.直立顺层边坡的粘弹性稳定性分析[J].力学与实践, 2003, 25(6):51~54.
ZHANG Tian-jun, LI Yun-peng. Linear viscoelasticity stability analysis of bluff rock slope[J]. Mechanics in Engineering, 2003, 25(6):51~54.
[9] 肖树芳, 杨淑碧.岩体力学[M].北京:地质出版社, 1987.
XIAO Shu-fang, YANG Shu-bi. Rock mass mechanics[M]. Beijing:Geological Publishing House, 1987.
[10] 张平占.BHA受压失稳的模型及临界钻压公式[J].煤田地质与勘探, 1995, 23(5):59~62. http://www.cnki.com.cn/Article/CJFDTOTAL-MDKT505.016.htm
ZHANG Ping-zhan. BHA's stability model and its critical load[J]. Coal Geology & Exploration, 1995, 23(5):59~62. http://www.cnki.com.cn/Article/CJFDTOTAL-MDKT505.016.htm
[11] Wang Z L, Li Y C, Wang J G. A damage-softening statistical constitutive model considering rock residual strength[J]. Computers & Geosciences, 2007, 33(1):1~9. http://www.sciencedirect.com/science/article/pii/S0098300406000380
[12] Li X, Cao W G, Su Y H. A statistical damage constitutive model for softening behavior of rocks[J]. Engineering Geology, 2012, 143:1~17. https://www.sciencedirect.com/science/article/pii/S0013795212001755
[13] 岳洋.基于不同分布的岩石损伤本构模型的比较[J].山西建筑, 2010, 36(24):137~138. doi: 10.3969/j.issn.1009-6825.2010.24.086
YUE Yang. Comparison of damage constitutive model of rock mass based on different distribution[J]. Shanxi Architecture, 2010, 36(24):137~138. doi: 10.3969/j.issn.1009-6825.2010.24.086
-



 下载:
下载: