Numerical simulation of crystallization blocking in tunnel drainage pipes based on dynamic mesh and level set
-
摘要:
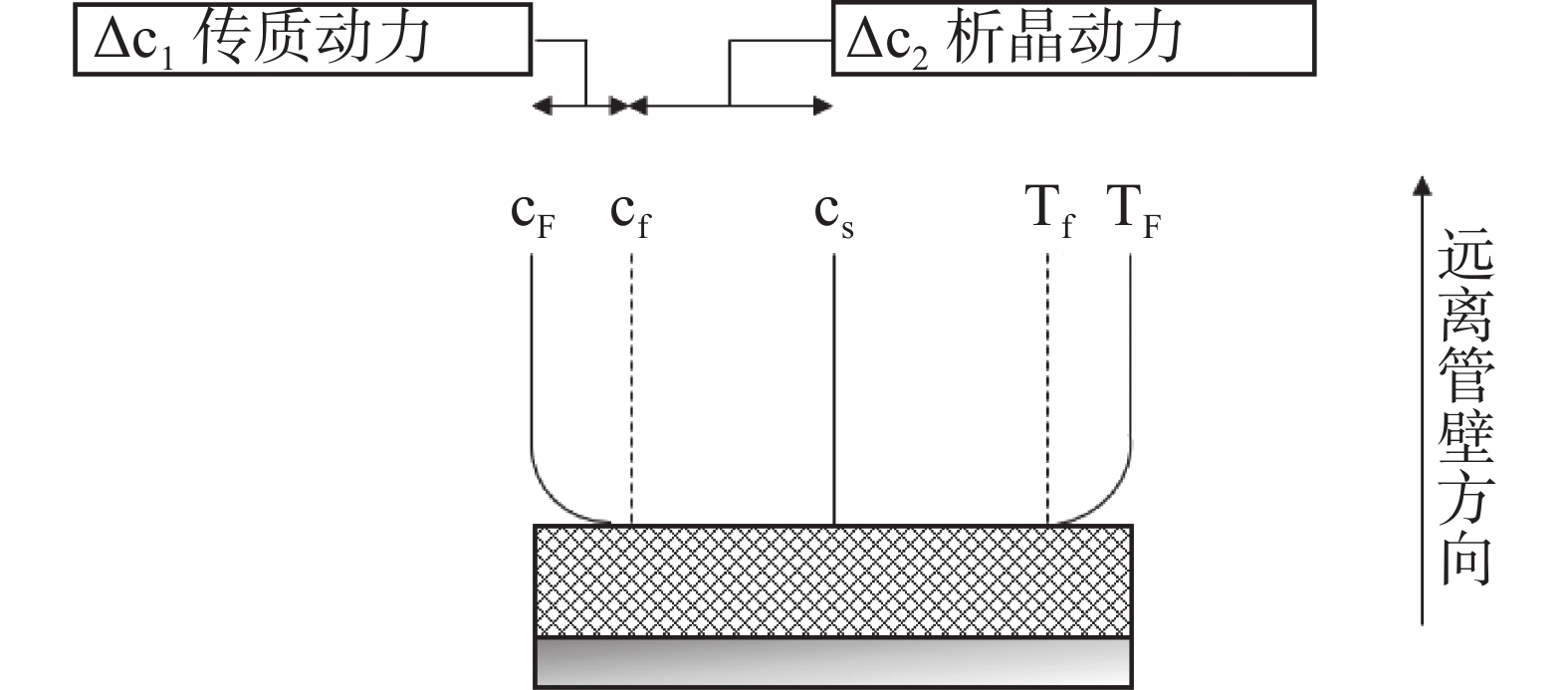
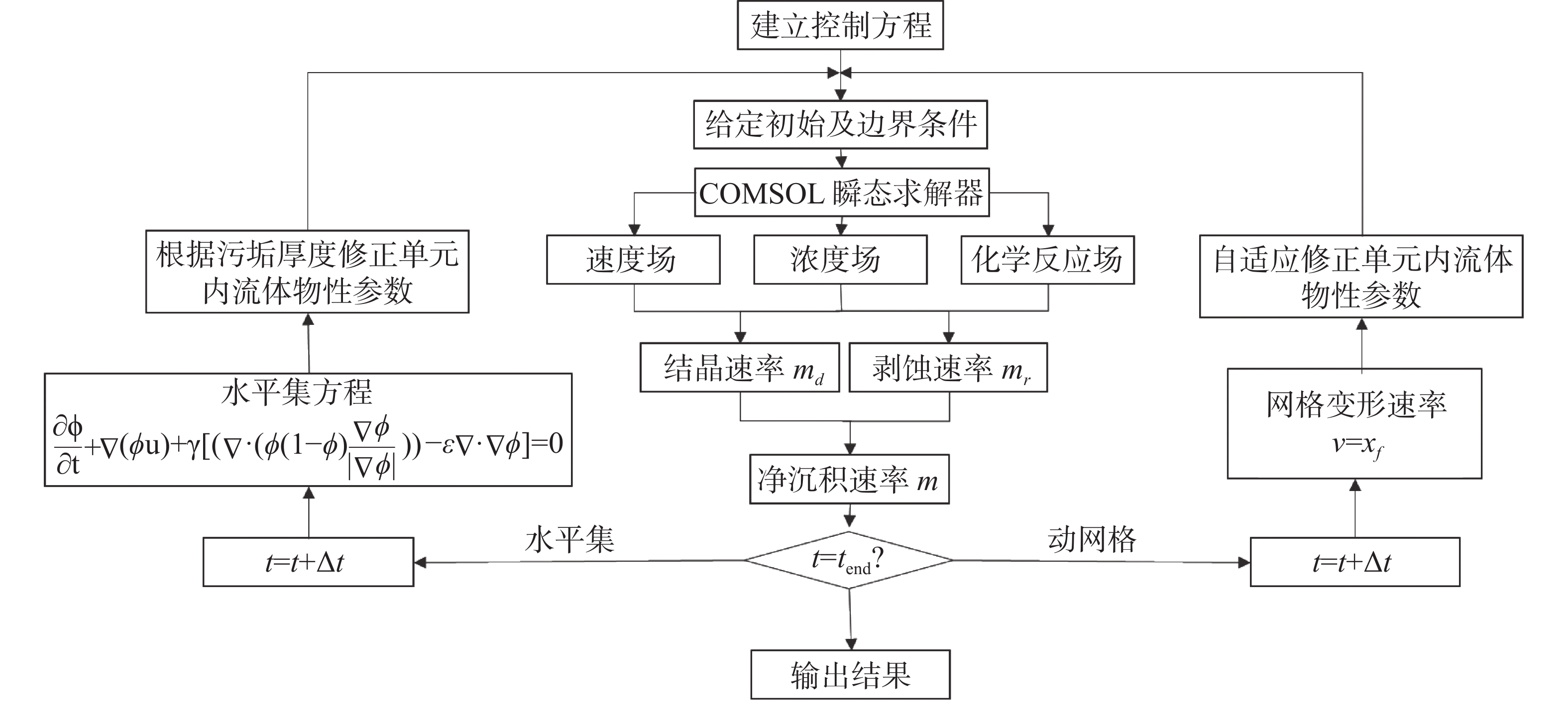
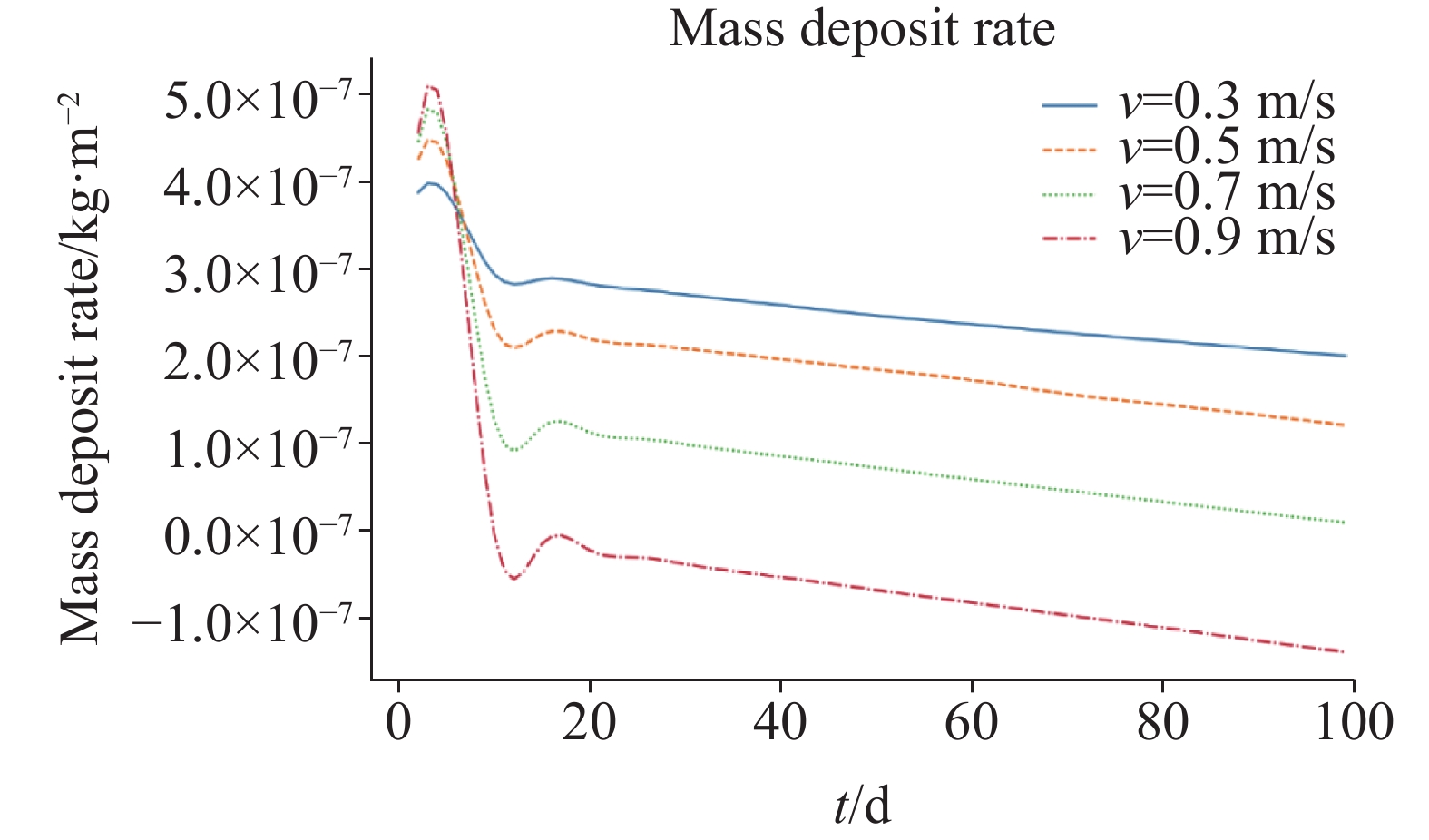
岩溶隧址区含水层内的高矿化度地下水渗入排水管道中,由于温压条件的改变,会导致渗流结晶从而堵塞排水管道。为定量化研究隧道排水系统结晶堵塞过程,本文首次构建了考虑管道水动力场、浓度场和化学反应场耦合的排水管岩溶水结晶堵塞模型,采用动网格和水平集方法定量刻画隧道排水系统结晶堵塞过程,开展模拟对比研究,分析温度、流速和溶液浓度等因素对结晶堵塞的影响程度。结果表明:(1)两种方法均能实现结晶堵塞过程的模拟预测,其中动网格方法建模简单,且求解精度高;水平集方法可追踪拓扑结构的变化,模拟管道完全堵塞的过程;(2)纵管内流速普遍大于横管,横管内CaCO3晶体浓度高于纵管,因此结晶堵塞主要发生于横管中;(3)温度和溶液浓度与结晶速率呈正相关关系,管内流速与结晶速率呈负相关关系。本文构建的考虑水动力−化学反应耦合的结晶堵塞数值模型可为岩溶隧道堵塞早期识别与安全评价提供技术支撑。
Abstract:The complex hydrogeological conditions in karst areas lead to frequent water seepage and water gushing disasters in tunnels, which often require supporting drainage systems to prevent and control water hazards. When the karst groundwater with high salinity enters the tunnel drainage pipe, the solubility of soluble salt ions in water changes with the variation of external temperature and pressure conditions, forming saturated solution. Ions crystallize and precipitate, sticking to the inner wall of the drainage pipe, which will contribute to decreasing its flow area. If not treated, in the long run, the drainage pipe will be blocked, resulting in the increase of water pressure in the tunnel lining. Consequently, it is likely to occur a series of tunnel water hazards such as water leakage, water gushing, mud outburst, lining damage, etc., which may seriously threaten the safety of tunnel construction and operation.
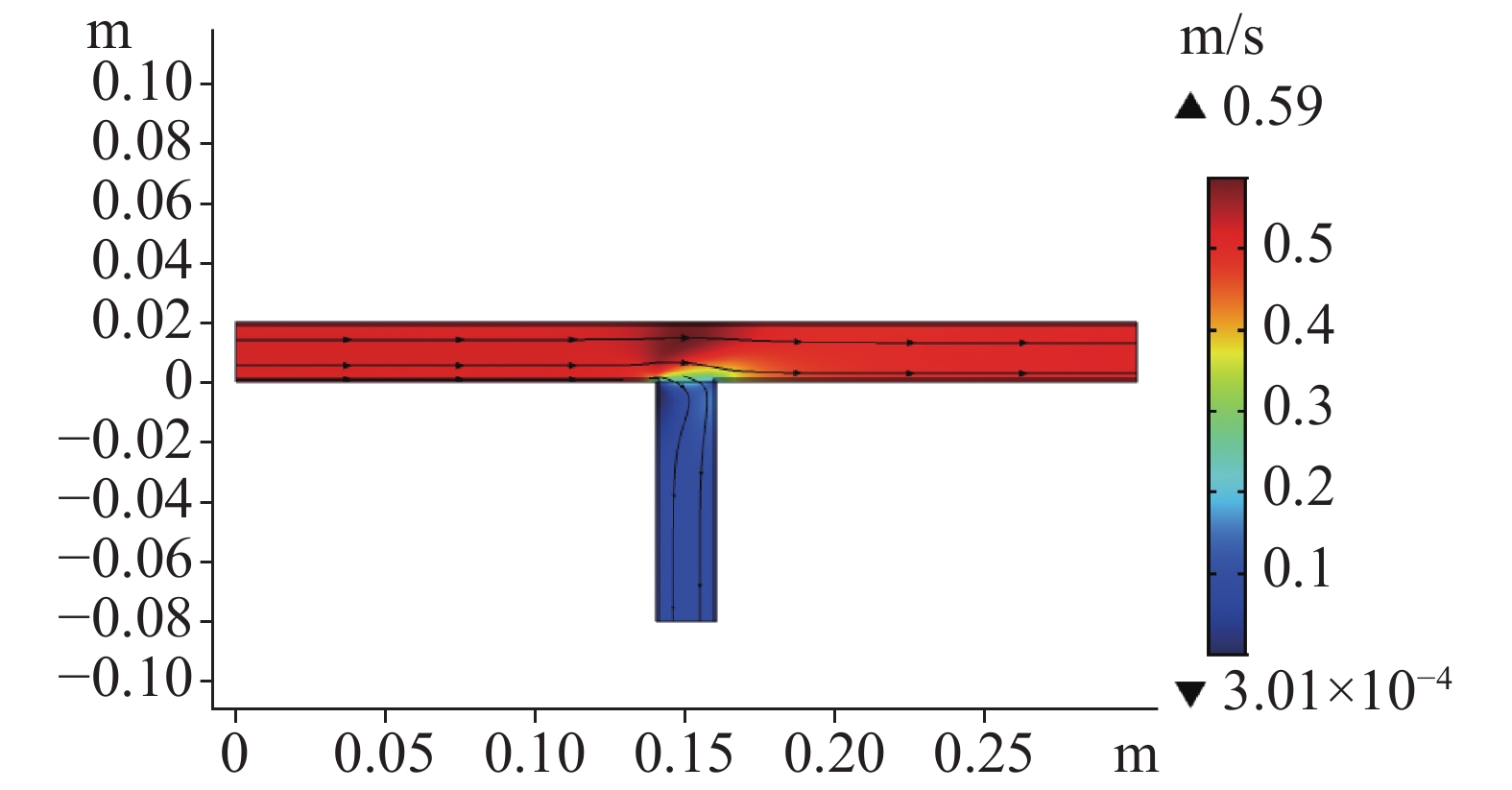
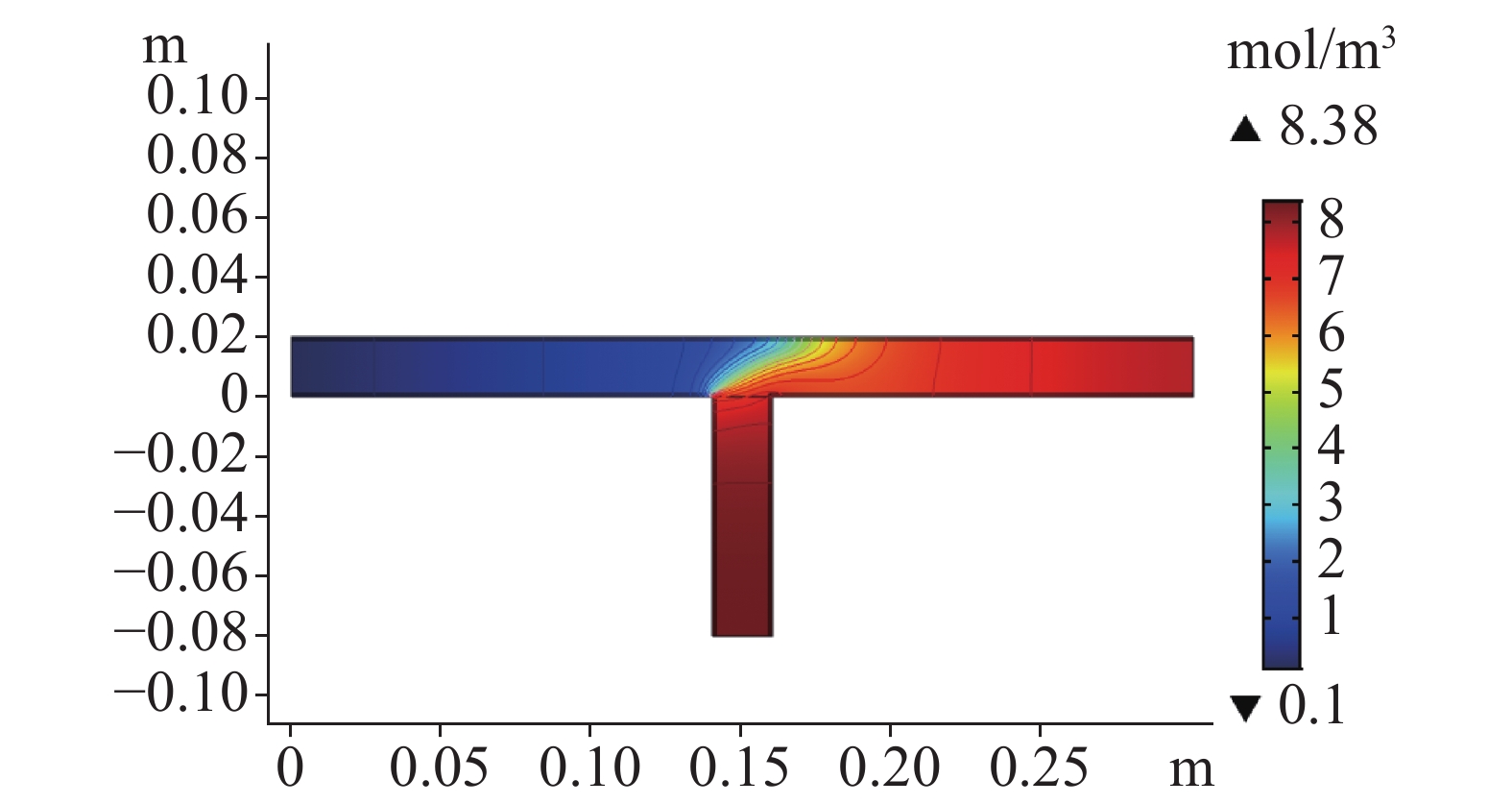
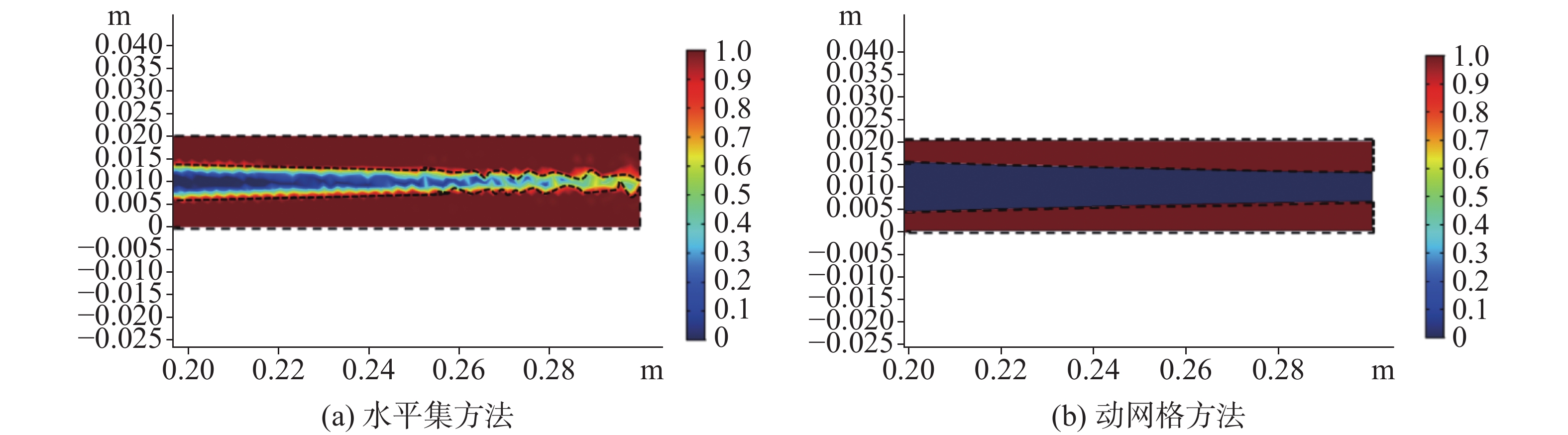
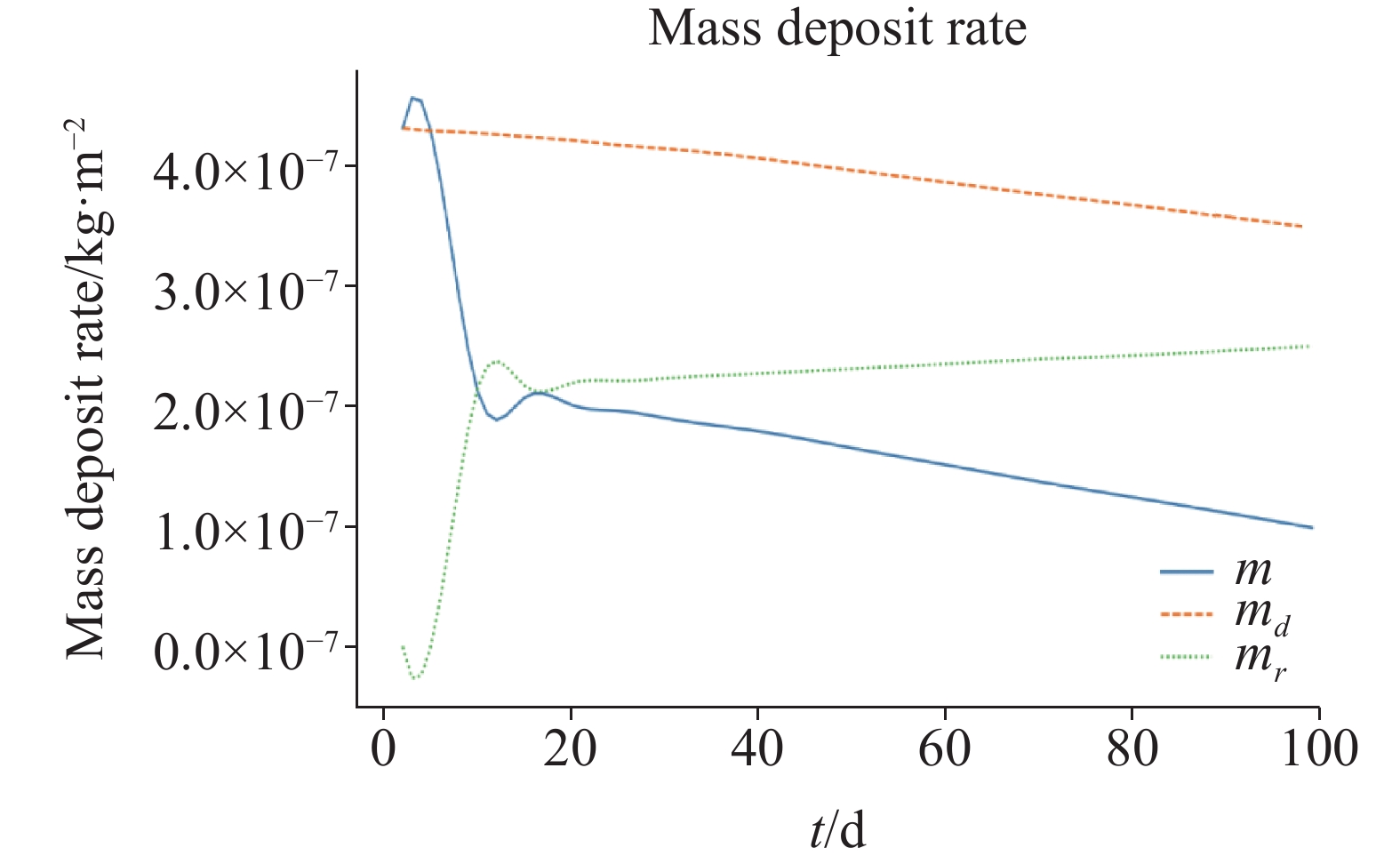
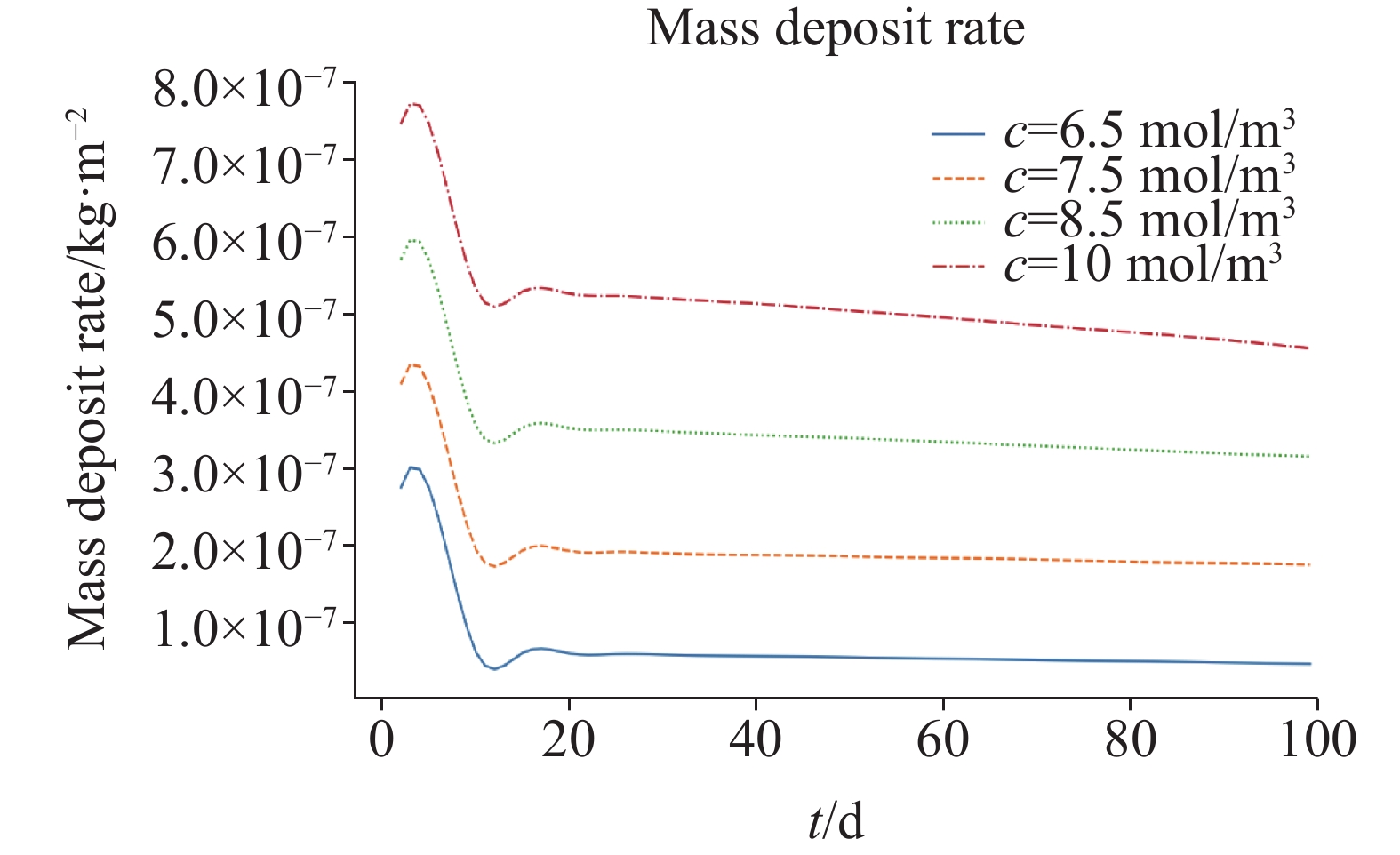
For quantitative research on the crystallization blocking process of tunnel drainage system, we constructed the blocking model of karst water crystallization in drainage pipes for the first time, coupling with the pipeline hydrodynamic field, the concentration field and the chemical reaction field. Meanwhile, with methods of dynamic mesh and level set, we quantitatively expounded the crystallization blocking process in the tunnel drainage system. We also carried out a comparative study on different simulation technologies to analyze the influence of such factors as temperature, velocity, solute concentration, etc. on the blocking of crystallization. The results show that: (1) Both of the two methods can simulate and predict the crystallizing process, among which the dynamic mesh method is simpler and its solving accuracy is relatively higher, and the level set method can be used to simulate the further deposition after the topological shape has been changed (i.e., completely blocked). (2) Crystallization blocking mainly occurs in the transverse tube, where more crystalline precipitates are developed, because the flow velocity in the longitudinal tube is generally higher than that in the transverse tube, and the CaCO3 crystal concentration in the transverse tube is higher than that in the longitudinal tube. (3) Temperatures and solution concentrations are positively correlated with the crystallization rate, while the flow rate is negatively correlated with it. (4) Given the coupling of hydrodynamic reaction with chemical reactions, the numerical model of crystallization blocking can provide technical support for the early identification and safety evaluation of geological hazards of karst tunnels.
-
Key words:
- karst tunnel /
- crystallization blocking /
- numerical simulation /
- dynamic mesh /
- level set
-

-
表 1 模型边界条件设定
Table 1. Setting of model boundary conditions
边界 物理场类型 流场 浓度场 入口 给定流速/流量 给定浓度/通量 出口 自由流出(p = 0) 自由流出(p = 0) 管壁 无滑移 无通量 表 2 模型参数
Table 2. Model parameters
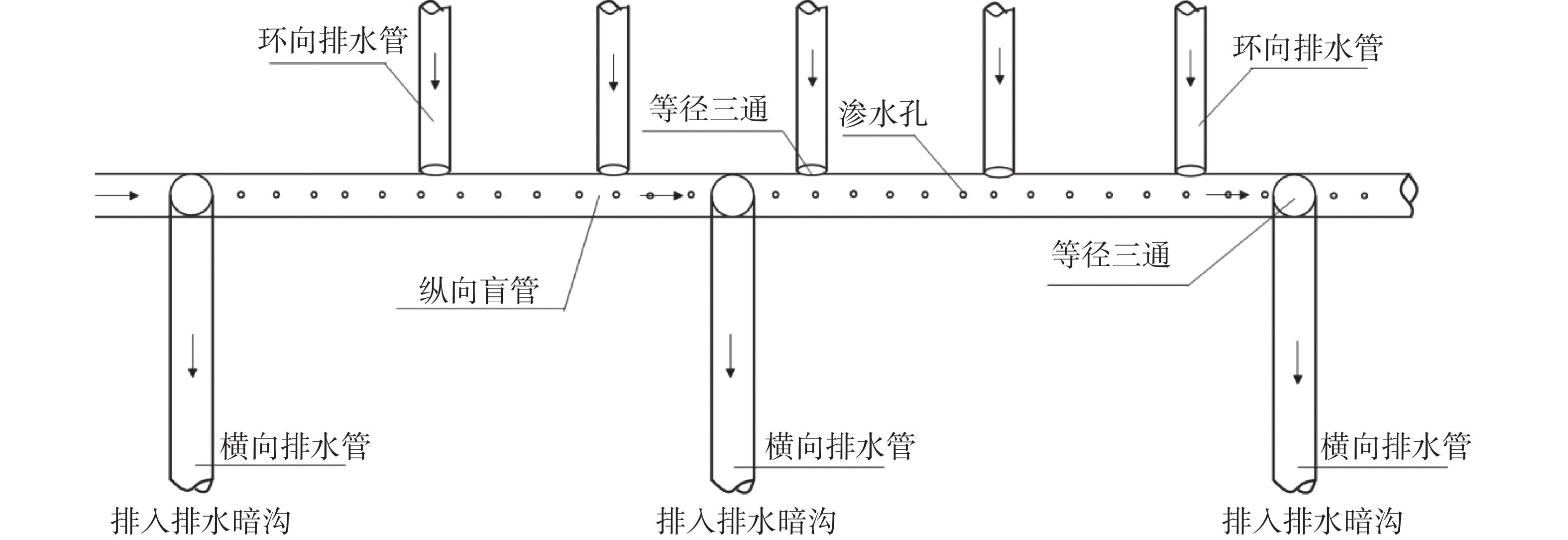
管型 形状 长度/mm 直径/mm 纵管 光滑圆管
光滑圆管300 2 横管 80 2 表 3 模型模拟工况设定
Table 3. Setting of model simulation conditions
工况 空白组 对照组 压力/atm 1 1 温度/K 293.15 273.15、283.15、303.15 入口浓度(以Ca2+计)/
mol·m−38.5 6.5、7.5、10 入口流速/m·s−1 0.541 0.3、0.7、0.9 -
[1] 袁道先, 章程. 岩溶动力学的理论探索与实践[J]. 地球学报, 2008, 29(3):355-365. doi: 10.3321/j.issn:1006-3021.2008.03.009
YUAN Daoxian, ZHANG Cheng. Karst Dynamics Theory in China and its practice[J]. Acta Geoscientica Sinica, 2008, 29(3):355-365. doi: 10.3321/j.issn:1006-3021.2008.03.009
[2] 周卓. 岩溶地区地下水渗流结晶堵塞隧道排水管机理研究及处治建议[D]. 西安: 长安大学, 2015.
ZHOU Zhuo. Study on the plug of the tunnel drainage pipe mechanism caused by groundwater seepage crystallization in karst area and the proposal of treatment[D]. Xi'an: Chang'an University, 2015.
[3] 向立辉. 富水隧道排水盲管堵塞效应分析及防治[D]. 重庆: 重庆交通大学, 2018.
XIANG Lihui. Analysis and prevention of tunnel drainage pipe blockage effect in water rich region[D]. Chongqing: Chongqing Jiaotong University, 2018.
[4] 宋焕荣, 黄尚瑜. 碳酸盐的结晶沉淀[J]. 中国岩溶, 1990, 9(2):3-16.
SONG Huanrong, HUANG Shangyu. Crystallized precipitation of carbonate[J]. Carsologica Sinica, 1990, 9(2):3-16.
[5] Plummer L, Wigley T, Parkhurst D. The kinetics of calcite dissolution in CO2-water systems at 5 ℃ to 60 ℃ and 0.0 to 1.0 atm CO2[J]. American Journal of Science, 1978, 278(2):179-216. doi: 10.2475/ajs.278.2.179
[6] Dreybrodt W, Buhmann D. A mass transfer model for dissolution and precipitation of calcite from solutions in turbulent motion[J]. Chemical Geology, 1991, 90(1-2):107-122.
[7] 刘再华, Dreybrodt W. DBL理论模型及方解石溶解、沉积速率预报[J]. 中国岩溶, 1998, 12(1):3-9.
LIU Zaihua, Dreybrodt W. The DBL model and prediction of calcite dissolution/precipitation rates[J]. Carsologica Sinica, 1998, 12(1):3-9.
[8] Epstein N. Fouling in heat exchangers[C]. Proceedings of the 6th International Heat Transfer Conference, 1986, 6: 235-253.
[9] 叶飞, 田崇明, 何彪, 赵猛, 王坚, 韩兴博, 宋桂锋. 在建隧道排水系统结晶堵塞试验[J]. 中国公路学报, 2021, 34(3):159-170.
YE Fei, TIAN Chongming, HE Biao, ZHAO Meng, Wang Jian, HAN Xingbo, SONG Guifeng. Experimental study on scaling and clogging in drainage system of tunnels under construction[J]. China Journal of Highway and Transport, 2021, 34(3):159-170.
[10] 高国红. 富水公路隧道排水系统结晶堵塞典型病害分析与处置[J]. 公路交通科技(应用技术版), 2020, 16(3):250-251.
GAO Guohong. Analysis and treatment of typical crystallization blocking disease of tunnel drainage system in water rich region of highway[J]. Journal of Highway and Transportation Research and Development (Applied Technology Edition), 2020, 16(3):250-251.
[11] 蒋雅君, 杜坤, 陶磊, 赵菊梅, 肖华荣. 岩溶隧道排水系统堵塞机理的调查与分析[J]. 铁道标准设计, 2019, 63(7):131-135.
JIANG Yajun, DU Kun, TAO Lei, ZHAO Jumei, XIAO Huarong. Investigation and discussion on blocking mechanism of drainage system in karst tunnels[J]. Railway Standard Design, 2019, 63(7):131-135.
[12] 刘士洋, 高峰, 周元辅, 刘强, 吕获印, 王博, 向坤, 肖东杰. 绒毛长度对隧道植绒排水管防除结晶效果试验[J]. 科学技术与工程, 2019, 19(9):234-239. doi: 10.3969/j.issn.1671-1815.2019.09.037
LIU Shiyang, GAO Feng, ZHOU Yuanfu, LIU Qiang, LYU Huoyin, WANG Bo, XIANG Kun, XIAO Dongjie. Effect of fuzz length on the prevention of crystallization of tunnel flocking drainpipes[J]. Science Technology and Engineering, 2019, 19(9):234-239. doi: 10.3969/j.issn.1671-1815.2019.09.037
[13] Hasson D, Avriel M, Resnick W, Rozenman T, Windreich S. Mechanism of calcium carbonate scale deposition on heat-transfer surfaces[J]. Industrial and Engineering Chemistry Fundamentals, 1968, 7(1):59-65.
[14] Bohnet M. Fouling of heat transfer surfaces[J]. Chemical Engineering & Technology, 1987, 10(1):113-125. doi: 10.1002/ceat.270100115
[15] Brahim F, Augustin W, Bohnet M. Numerical simulation of the fouling process[J]. International Journal of Thermal Sciences, 2003, 42(3):323-334. doi: 10.1016/S1290-0729(02)00021-2
[16] Brahim F, Augustin W, Bohnet M. Numerical simulation of the fouling on structured heat transfer surfaces (fouling)[J]. Proceedings of Heat Exchanger Fouling and Cleaning: Fundamentals and Applications, 2004:17.
[17] 徐志明, 张仲彬, 程浩明. 管内CaCO3污垢形成过程的数值模拟[J]. 工程热物理学报, 2009, 30(12):2099-2101. doi: 10.3321/j.issn:0253-231X.2009.12.034
XU Zhiming, ZHANG Zhongbin, CHENG Haoming. Numerical simulation of CaCO3 fouling process in a tube[J]. Journal of Engineering Thermophysics, 2009, 30(12):2099-2101. doi: 10.3321/j.issn:0253-231X.2009.12.034
[18] 徐志明, 张进朝, 张仲彬, 白珊. 圆管内CaSO4析晶污垢模型与数值模拟[J]. 化学工程, 2009, 37(7):13-16. doi: 10.3969/j.issn.1005-9954.2009.07.004
XU Zhiming, ZHANG Jinchao, ZHANG Zhongbin, BAI Shan. Model and numerical simulation of CaSO4 crystallization fouling in circular tube[J]. Chemical Engineering, 2009, 37(7):13-16. doi: 10.3969/j.issn.1005-9954.2009.07.004
[19] 徐志明, 朱宏娟, 张一龙. 直角弯管硫酸钙污垢沉积特性研究[J]. 东北电力大学学报, 2014(3):7-13. doi: 10.3969/j.issn.1005-2992.2014.04.007
XU Zhiming, ZHU Hongjuan, ZHANG Yilong. Research of CaSO4 fouling in right-angle pipe bends[J]. Journal of Northeast Electric Power University, 2014(3):7-13. doi: 10.3969/j.issn.1005-2992.2014.04.007
[20] 李竑序. 管壁材质对碳酸钙垢生长的影响及其机理研究[D]. 兰州: 兰州交通大学, 2017.
LI Hongxu. The effect of tube wall material on growth of calcium carbonate fouling and its mechanism[D]. Lanzhou: Lanzhou Jiaotong University, 2017.
[21] 李竑序, 艾雄杰, 王良璧, 常立民, 王良成. 管壁材质对碳酸钙垢生长的影响及其机理研究[J]. 工程热物理学报, 2018, 39(12):2773-2778.
LI Hongxu, AI Xiongjie, WANG Liangbi, CHANG Limin, WANG Liangcheng. Effect of tube wall material on calcium carbonate scale growth and its mechanism[J]. Journal of Engineering Thermophysics, 2018, 39(12):2773-2778.
[22] 王磊, 赵莹, 徐凤煜. 换热面材质对硫酸钙结垢形态的影响试验研究[J]. 重庆电力高等专科学校学报, 2019, 24(5):21-23.
WANG Lei, ZHAO Ying, XU Fengyu. An experimental study of the influence of the materials of the heating surface on the scaling forms of CaSO4[J]. Journal of Chongqing Electric Power College, 2019, 24(5):21-23.
[23] Hasson D, Avriel M, Resnick W, Rozenman T, Windreich S. Calcium carbonate scale deposition on heat transfer surfaces[J]. Desalination, 1968, 5(1):107-119. doi: 10.1016/S0011-9164(00)80198-8
[24] M Förster, Augustin W, Bohnet M. Influence of the adhesion force crystal/heat exchanger surface on fouling mitigation[J]. Chemical Engineering and Processing Process Intensification, 1999, 38(4-6):449-461. doi: 10.1016/S0255-2701(99)00042-2
[25] Kern D Q, Seaton R E. A theoretical analysis of thermal surface fouling[J]. British Chemical Engineering, 1959, 4:258-262.
[26] 王险峰. 复空间形式中的拉格朗日子流形[D]. 北京: 清华大学, 2011.
WANG Xianfeng. Lagrangian submanifolds in complex space forms[D]. Beijing: Tsinghua University, 2011.
[27] 黄弘, 胡啸峰, 申世飞, 原智宏, 冈林一木, 大场良二. 基于Lagrangian模型与Eulerian模型耦合的建筑物周边气体扩散模拟[J]. 清华大学学报(自然科学版), 2011, 51(12):1870-1876.
HUANG Hong, HU Xiaofeng, SHEN Shifei, TOMOHIRO Hara, KAZUKI Okabayashi, RYOHJI Ohba. Simulation of pollutant diffusion based on Lagrangian/Eulerian hybrid model around buildings[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(12):1870-1876.
[28] 江帆, 陈维平, 王一军, 区嘉洁. 基于动网格的离心泵内部流场数值模拟[J]. 流体机械, 2007, 35(7):20-24.
JIANG Fan, CHEN Weiping, WANG Yijun, OU Jiajie. Numerical simulation of flow field inside of centrifugal pump based on dynamics mesh[J]. Fluid Machinery, 2007, 35(7):20-24.
[29] 童亮, 余罡, 彭政, 余江洪, 肖金生. 基于VOF模型与动网格技术的两相流耦合模拟[J]. 武汉理工大学学报(信息与管理工程版), 2008(4):525-528.
TONG Liang, YU Gang, PENG Zheng, YU Jianghong, XIAO Jinsheng. Coupled Simulation of two phase flow based on VOF model and dynamic mesh technology[J]. Journal of Wuhan University of Technology (Information and Management Engineering), 2008(4):525-528.
[30] Osher S, Sethian James A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49.
[31] Osher S, Fedkiw R, Piechor K. Level set methods and dynamic implicit surfaces[J]. Applied Mechanics Reviews, 2004, 57(3): B13-B17.
[32] 翟明. 灰岩区隧道排水系统结晶堵塞规律研究[D]. 重庆: 重庆交通大学, 2016.
ZHAI Ming. Study on the regularity of crystallization and blocking of tunnel drainage system in limestone area[D]. Chongqing: Chongqing Jiaotong University, 2016.
-




 下载:
下载: