基于逐级迭代插值的重力数据扩边方法研究

许海红; 王宝文; 周俊林; 姜亭; 韩小锋; 赵飞; 袁炳强; 马杰

doi:10.12401/j.nwg.2023014

基于逐级迭代插值的重力数据扩边方法研究

1.
中国地质调查局西安地质调查中心/西北地质科技创新中心，陕西西安　710054

2.
西安石油大学地球科学与工程学院，陕西西安　710065

3.
陕西省矿产地质调查中心，陕西西安　710068

基金项目: 中国地质调查局项目“全国氦气资源潜力评价与战略选区调查”（DD20221665），陕西省自然科学基础研究–面上项目“基于地球物理多元属性的银额盆地西部火成岩识别方法研究”（2023-JC-YB-273）联合资助。

详细信息

作者简介: 许海红（1984−），男，高级工程师，主要从事油气资源勘查研究工作。E–mail：honghaibeibei@163.com

通讯作者: 王宝文（1984−），男，高级工程师，主要从事油气资源潜力评价工作。E–mail：wang_bw@163.com

中图分类号: P631.1

收稿日期: 2022-06-08

修回日期: 2022-12-29

刊出日期: 2023-04-20

Research on the Method of Gravity Data Edge Expanding Based on Step By Step Iterative Interpolation

1.
Xi’an Center of Geological Survey / Northwest China Center for Geoscience Innovation, China Geological Survey, Xi’an 710054, Shaanxi, China

2.
School of Earth Sciences and Engineering, Xi’an Shiyou University, Xi’an 710065, Shaanxi, China

3.
Shaanxi Mineral Resources and Geological Survey, Xi’an 710068, Shaanxi, China

More Information

Corresponding author: WANG Baowen, wang_bw@163.com

Received Date: 08 June 2022

Revised Date: 29 December 2022

Publish Date: 20 April 2023

摘要

摘要:
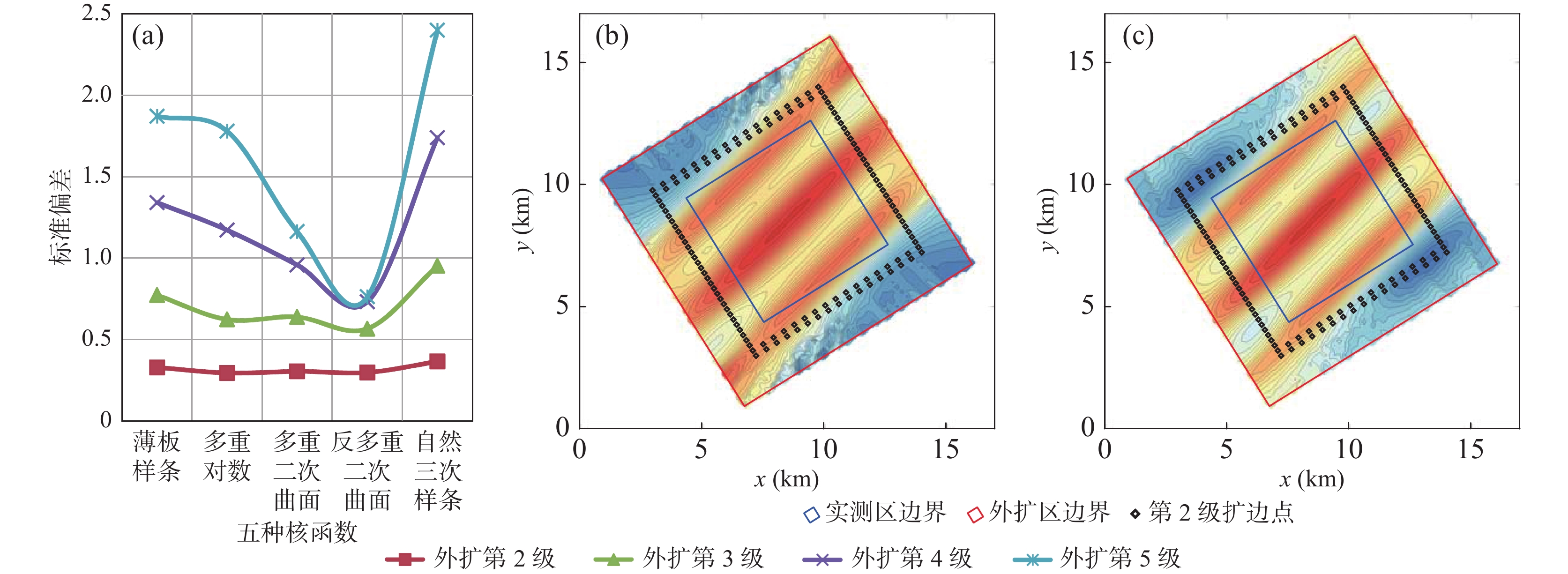
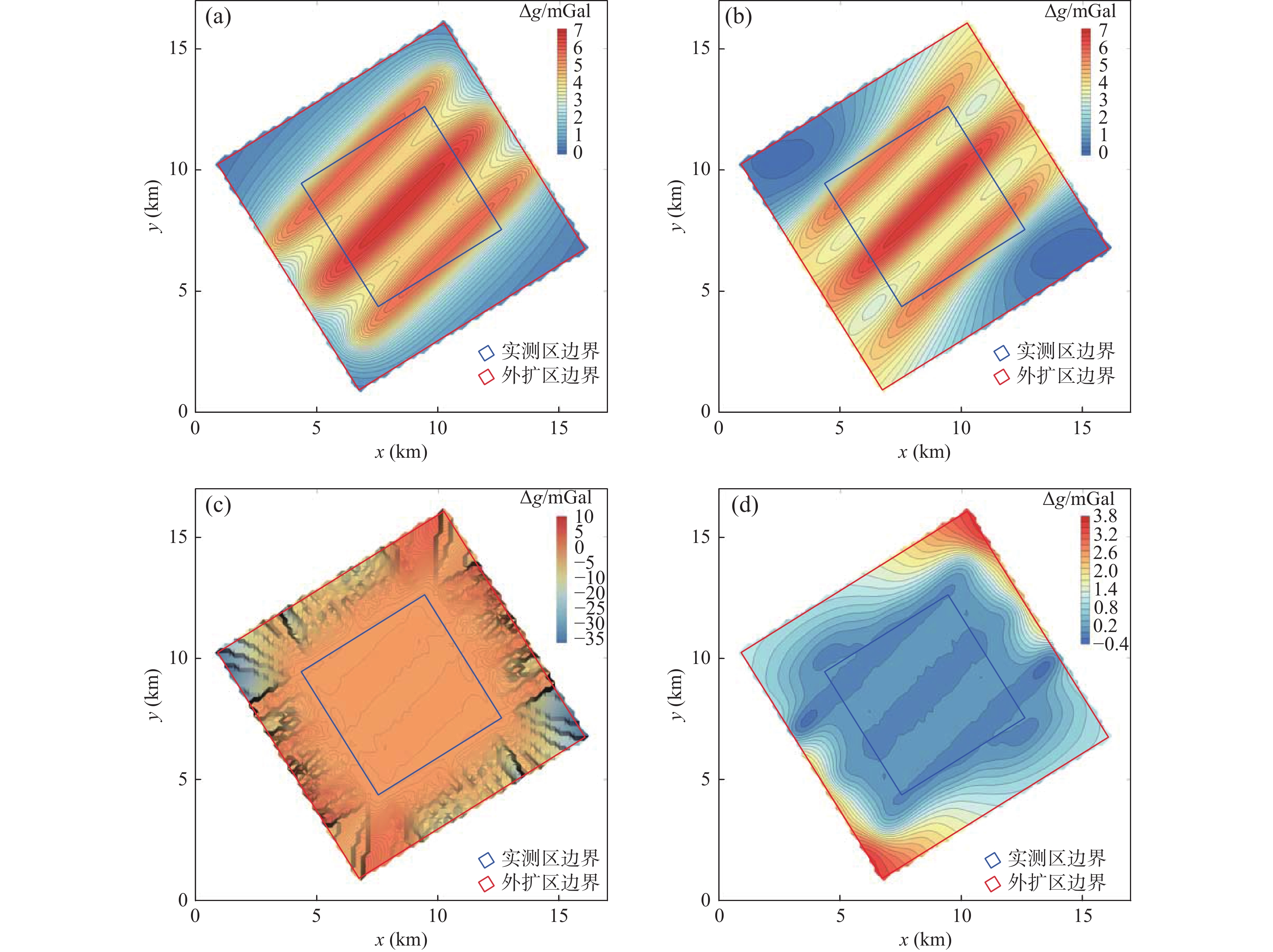
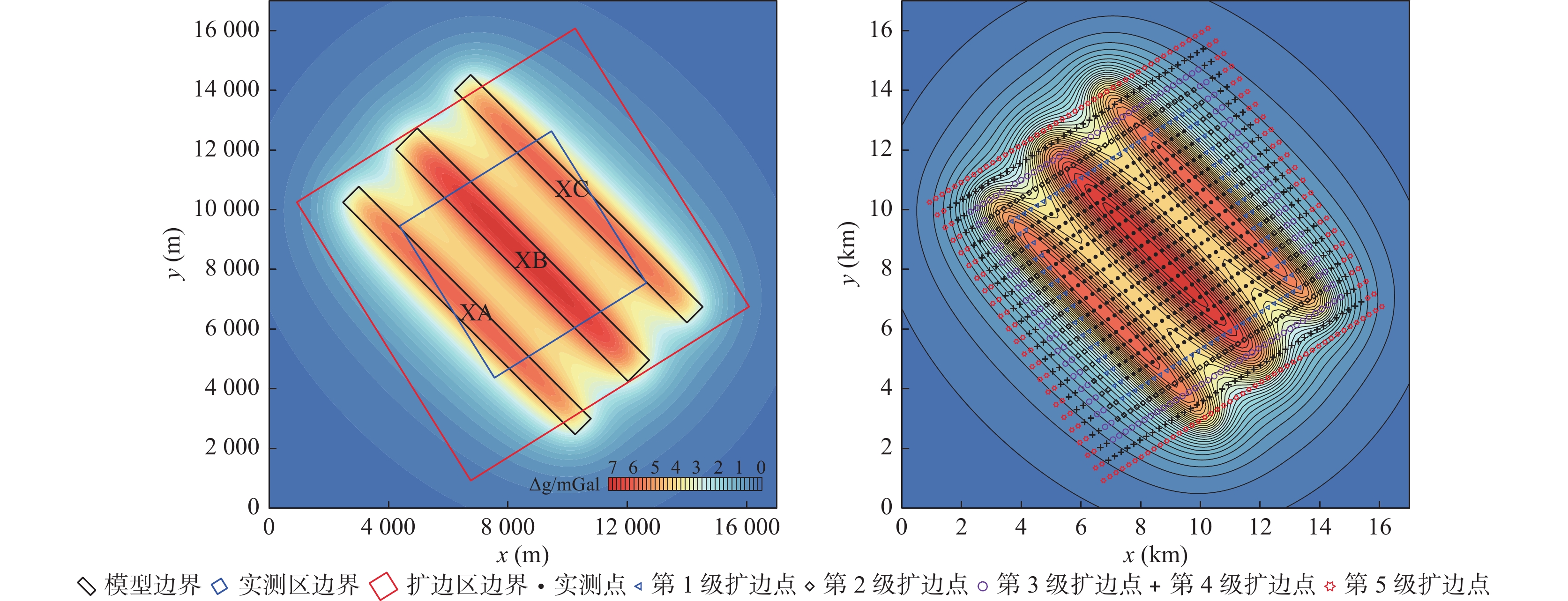
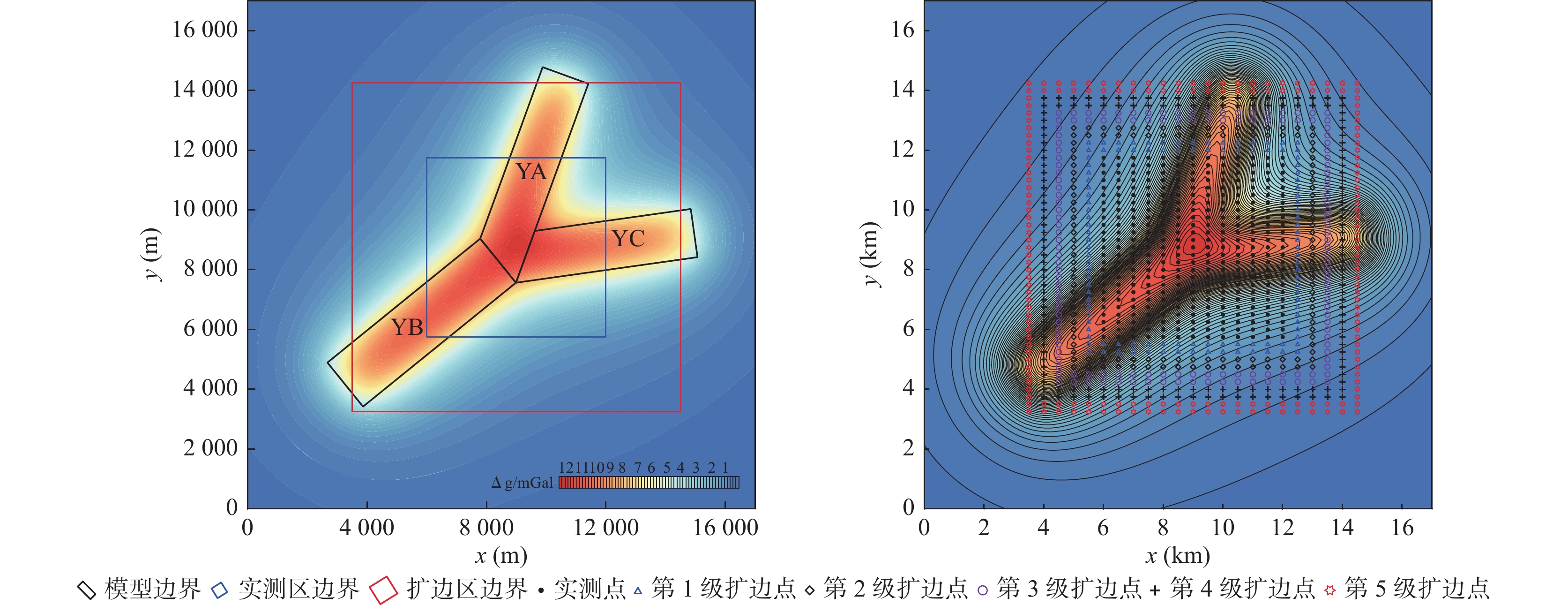
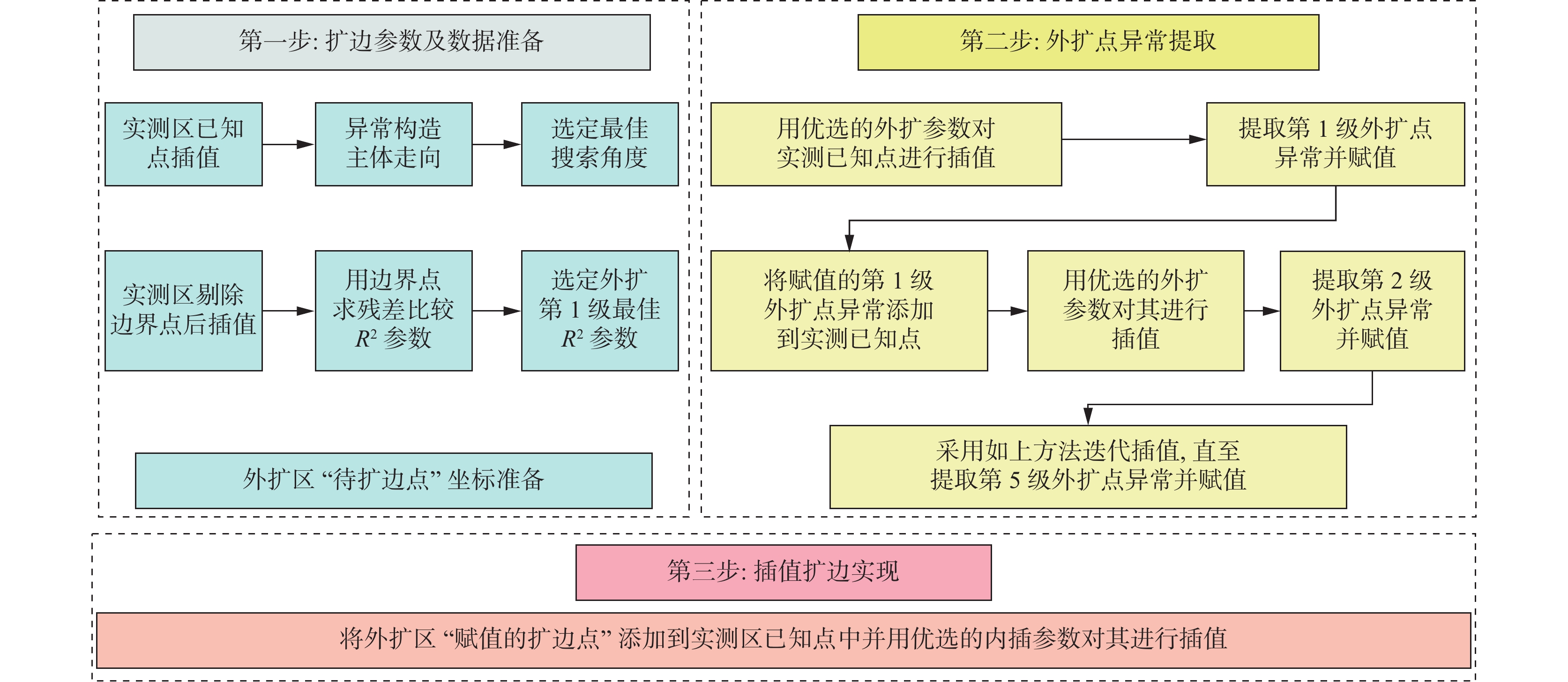
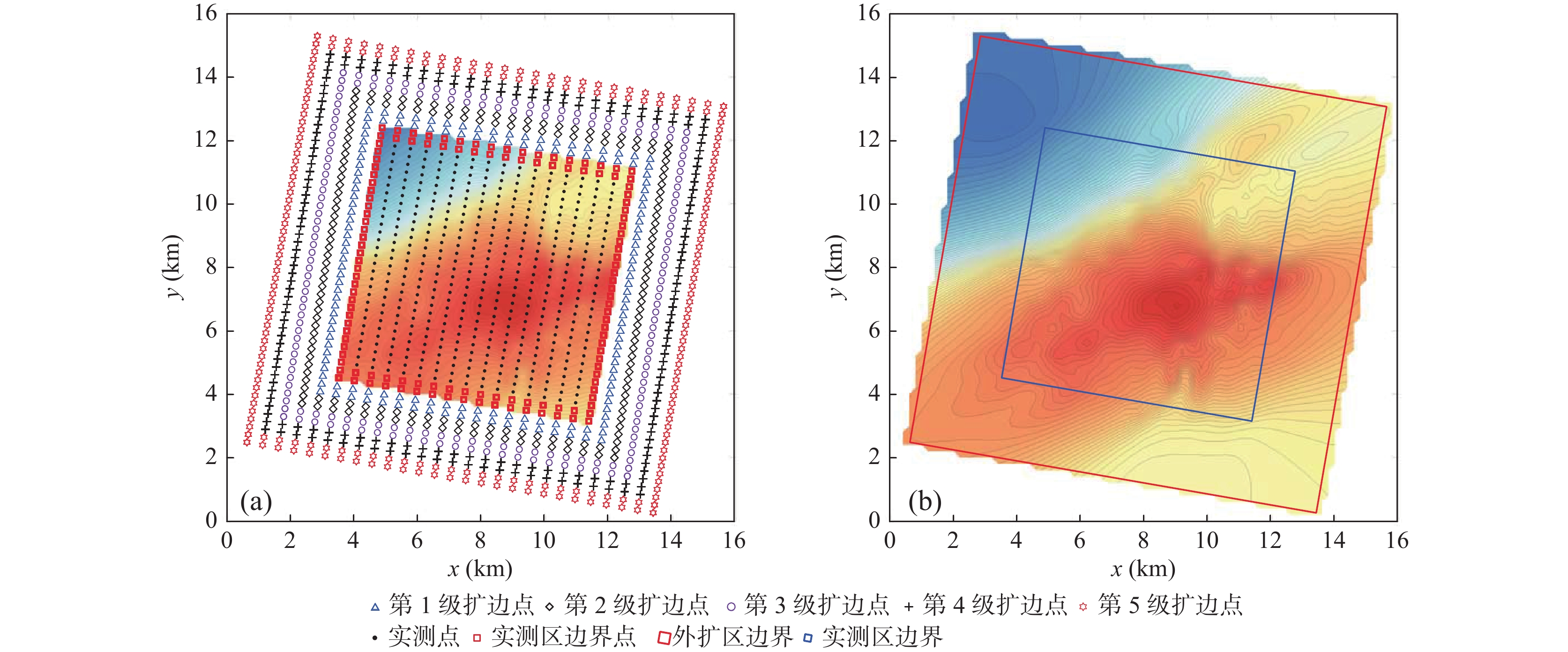
为了研究考虑异常变化特征的扩边插值方法，笔者使用理论重力异常模拟提取的1∶5万重力数据进行研究。通过Surfer软件中7种插值方法的比较，认为径向基函数法在数据扩边时能够获得较好的结果。在此基础上，笔者提出逐级迭代插值的思路并优选扩边参数如下：①核函数为多重二次曲面核函数。②搜索扇区为4个。③搜索点数为64个。④搜索半径R₁/R₂为6/18，且R₂平行于异常整体走向。⑤搜索角度选为当搜索半径长轴R₂平行于异常走向时的角度。⑥R²参数一般为0～1。其中，首次扩边时R²参数根据边界点残差对比结果选定，其余各级扩边时R²参数选0.1即可。银额盆地西部LY区块实际资料扩边应用时，采用“三步法”进行插值能够将外扩与内插参数联合考虑，扩边结果显示扩边区与实测区衔接处的重力异常连续光滑，扩边区较好的反映了异常整体趋势和局部变化特征。
- 重力数据 /
- 扩边方法 /
- 逐级迭代 /
- 插值参数
Abstract:
In order to study the edge expanding interpolation method considering the variation characteristics of gravity anomaly, we used 1∶50000 gravity data obtained from theoretical gravity anomaly simulation for research. Through the comparison of 7 interpolation methods in surfer software, it is considered that the radial basis function method can obtain better results in data expanding. On this basis, the idea of step by step iterative interpolation is proposed and the expanding parameters are optimized as follows: ① The kernel function is multiquadric function, ② The number of sectors to research is 4, ③ The maximum number of data to use from all sectors is 64, ④ The search radius R₁/R₂=6/18, and the radius R₂ parallels to the main strike of the anomaly, ⑤ The search angle was selected when the search radius R₂ is parallels to the main strike of the anomaly, ⑥ The R² parameter is generally between 0 and 1, among them, R² parameter is selected according to the residual error comparison results of boundary points when expanding for the first time, and 0.1 parameter can be selected for other levels of expanding. In the application of actual data edge expanding of LY block in west of Yin’e basin, the “three–step method” can be used for interpolation to jointly consider the external expanding and internal interpolation parameters. The expanding results show that the gravity anomaly at the junction of the expanding area and the measured area is continuous and smooth, and the expanding area better reflects the main strike and local variation characteristics of the anomaly.
- gravity data /
- edge expanding method /
- step by step iterative /
- interpolation parameters

HTML全文

图 1 理论模型重力异常及点位分布图

Figure 1.

下载: 全尺寸图片幻灯片

图 2 不同插值方法标准偏差曲线

Figure 2.

下载: 全尺寸图片幻灯片

图 3 5种核函数标准偏差曲线

Figure 3.

下载: 全尺寸图片幻灯片

图 4 不同R²标准偏差曲线

Figure 4.

下载: 全尺寸图片幻灯片

图 5 外扩第1级点的标准偏差曲线

Figure 5.

下载: 全尺寸图片幻灯片

图 6 半径R₁=6、R₂=12时外扩区标准偏差曲线

Figure 6.

下载: 全尺寸图片幻灯片

图 7 不同搜索半径外扩区标准偏差曲线

Figure 7.

下载: 全尺寸图片幻灯片

图 8 不同搜索点数外扩区标准偏差曲线

Figure 8.

下载: 全尺寸图片幻灯片

图 9 两组最优参数对应的外扩和内插结果

Figure 9.

下载: 全尺寸图片幻灯片

图 10 添加外扩第1级“赋值的扩边点”后不同核函数扩边结果

Figure 10.

下载: 全尺寸图片幻灯片

图 11 添加“赋值的扩边点”后不同R²参数扩边的标准偏差曲线

Figure 11.

下载: 全尺寸图片幻灯片

图 12 不同搜索参数对应的标准偏差曲线

Figure 12.

下载: 全尺寸图片幻灯片

图 13 添加“赋值的扩边点”前后扩边结果对比

Figure 13.

下载: 全尺寸图片幻灯片

图 14 新模型及其理论重力异常

Figure 14.

下载: 全尺寸图片幻灯片

图 15 不同搜索角度时新模型的标准偏差曲线

Figure 15.

下载: 全尺寸图片幻灯片

图 16 Y模型及其理论重力异常

Figure 16.

下载: 全尺寸图片幻灯片

图 17 不同搜索角度时Y模型的标准偏差曲线

Figure 17.

下载: 全尺寸图片幻灯片

图 18 新模型（a）与Y模型（b）不同搜索半径的扩边结果

Figure 18.

下载: 全尺寸图片幻灯片

图 19 新模型（a）与Y模型（b）不同搜索点数的扩边结果

Figure 19.

下载: 全尺寸图片幻灯片

图 20 逐级迭代插值扩边流程图

Figure 20.

下载: 全尺寸图片幻灯片

图 21 LY区块扩边前（a）后（b）等值线图

Figure 21.

下载: 全尺寸图片幻灯片

表 1 理论模型参数

Table 1. Parameters of the theoretical model

模型编号	角点坐标（m）	顶面埋深（m）	底面埋深（m）	密度差（g/cm³）
A	（10774，14001），（10244，14532），（2466，6754），（2996，6223）	500	1500	0.5
B	（12731，12047），（12024，12755），（4246，4976），（4953，4269）	600	1600	0.5
C	（14521，10254），（13990，10785），（6212，3007），（6742，2476）	500	1500	0.5

下载: 导出CSV

表 2 不同插值方法标准偏差结果

Table 2. Standard deviation results of different interpolation methods

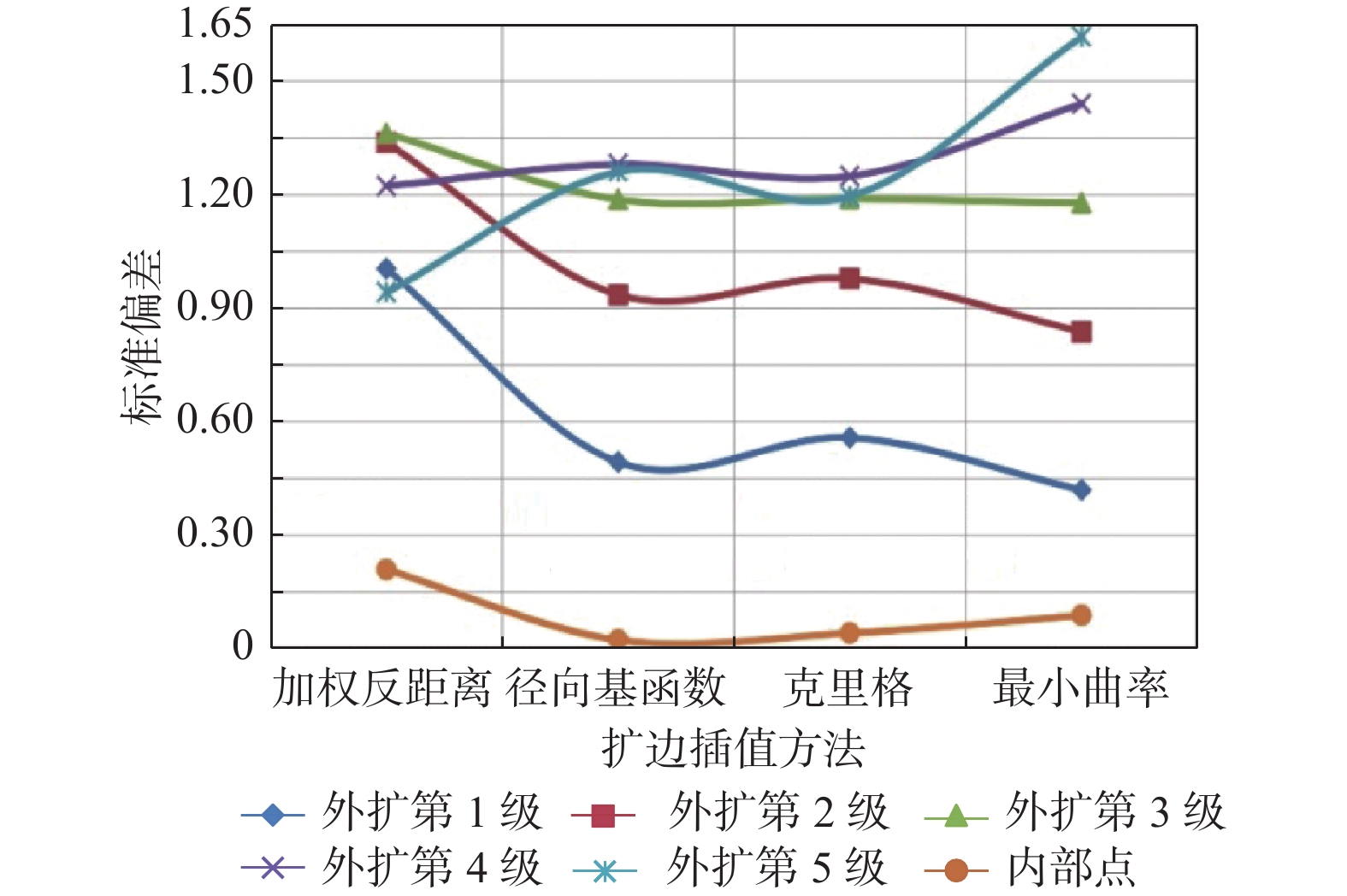
插值方法	内部点	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
带线性插值的三角剖分法	0.0412	#N/A	#N/A	#N/A	#N/A	#N/A
自然邻点	0.0497	#N/A	#N/A	#N/A	#N/A	#N/A
改进谢别德	133	11593	32642	5	#N/A	#N/A
加权反距离	0.2093	1.0056	1.3398	1.3628	1.2244	0.9430
径向基函数	0.0230	0.4938	0.9367	1.1888	1.2818	1.2625
克里格	0.0415	0.5584	0.9797	1.1909	1.2506	1.1969
最小曲率	0.0882	0.4198	0.8386	1.1797	1.4419	1.6196
注：#N/A 表示在扩边区未形成“扩边值” 。

下载: 导出CSV

表 3 5种核函数标准偏差结果

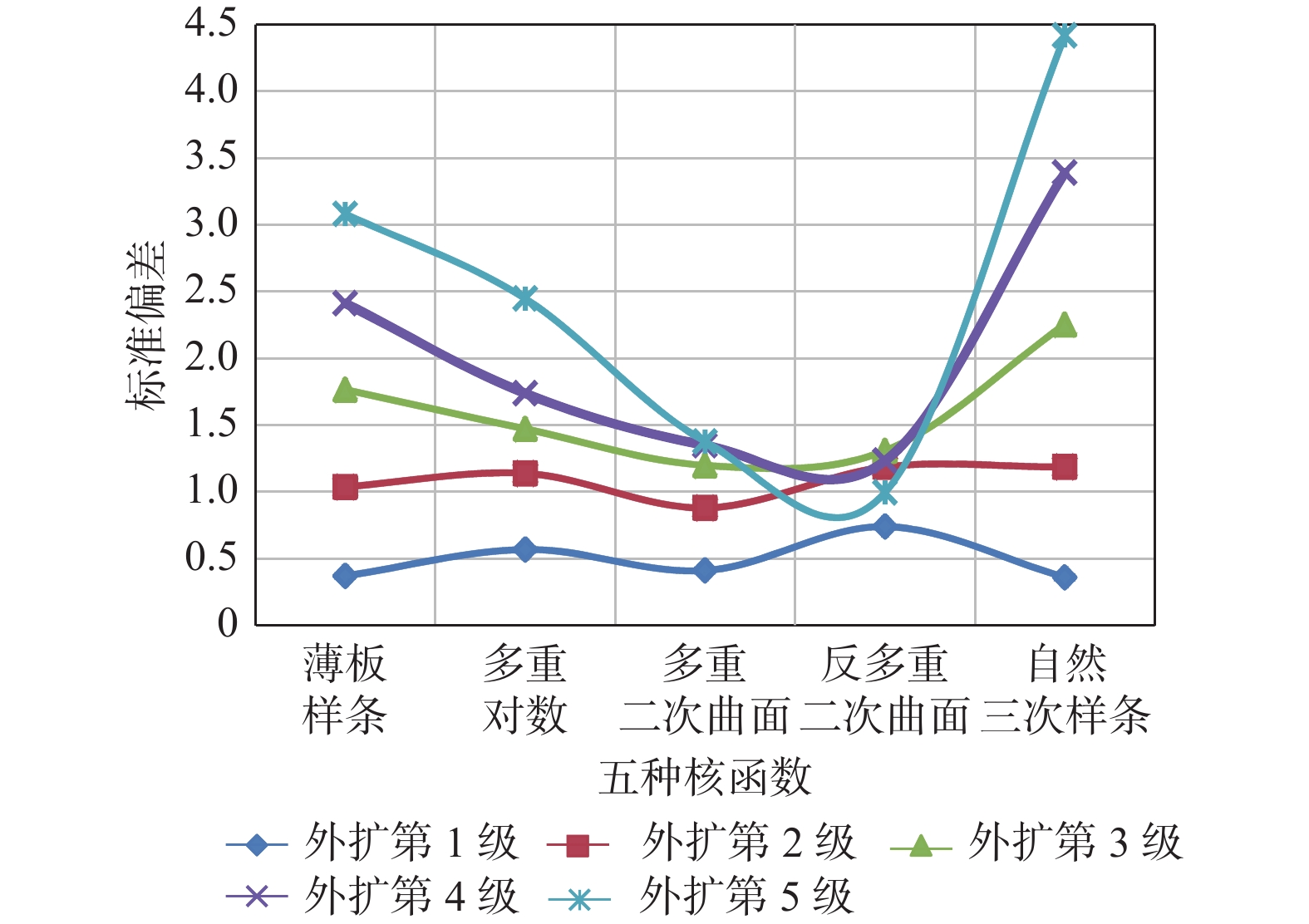
Table 3. Standard deviation results of five kernel functions

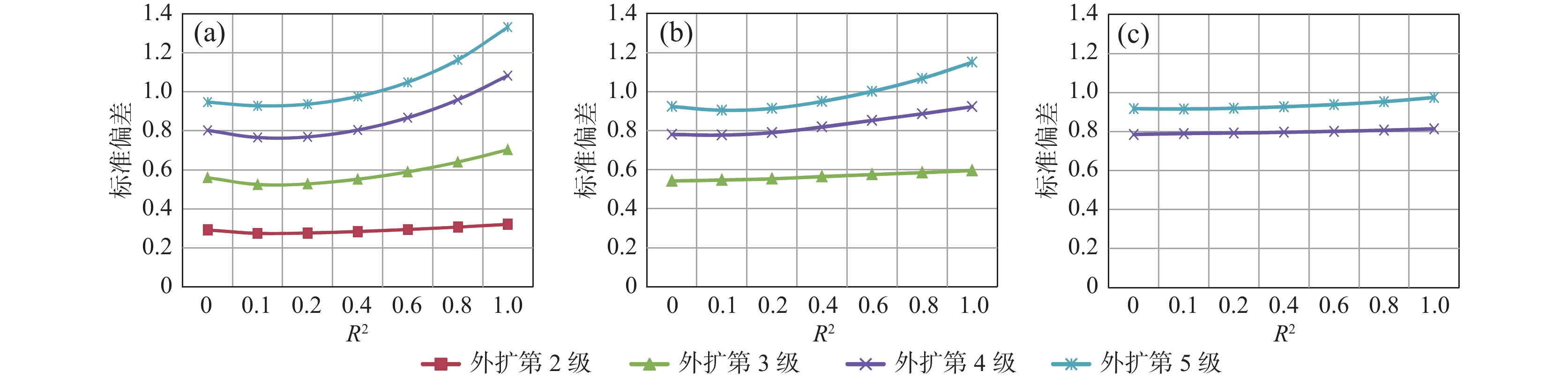
核函数	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
薄板样条	0.3685	1.0353	1.7646	2.4110	3.0803
多重对数	0.5662	1.1369	1.4705	1.7352	2.4457
多重二次曲面	0.4087	0.8779	1.1968	1.3479	1.3751
反多重二次曲面	0.7376	1.1848	1.3064	1.2313	0.9944
自然三次样条	0.3575	1.1839	2.2529	3.3890	4.4181

下载: 导出CSV

表 4 不同R²标准偏差结果

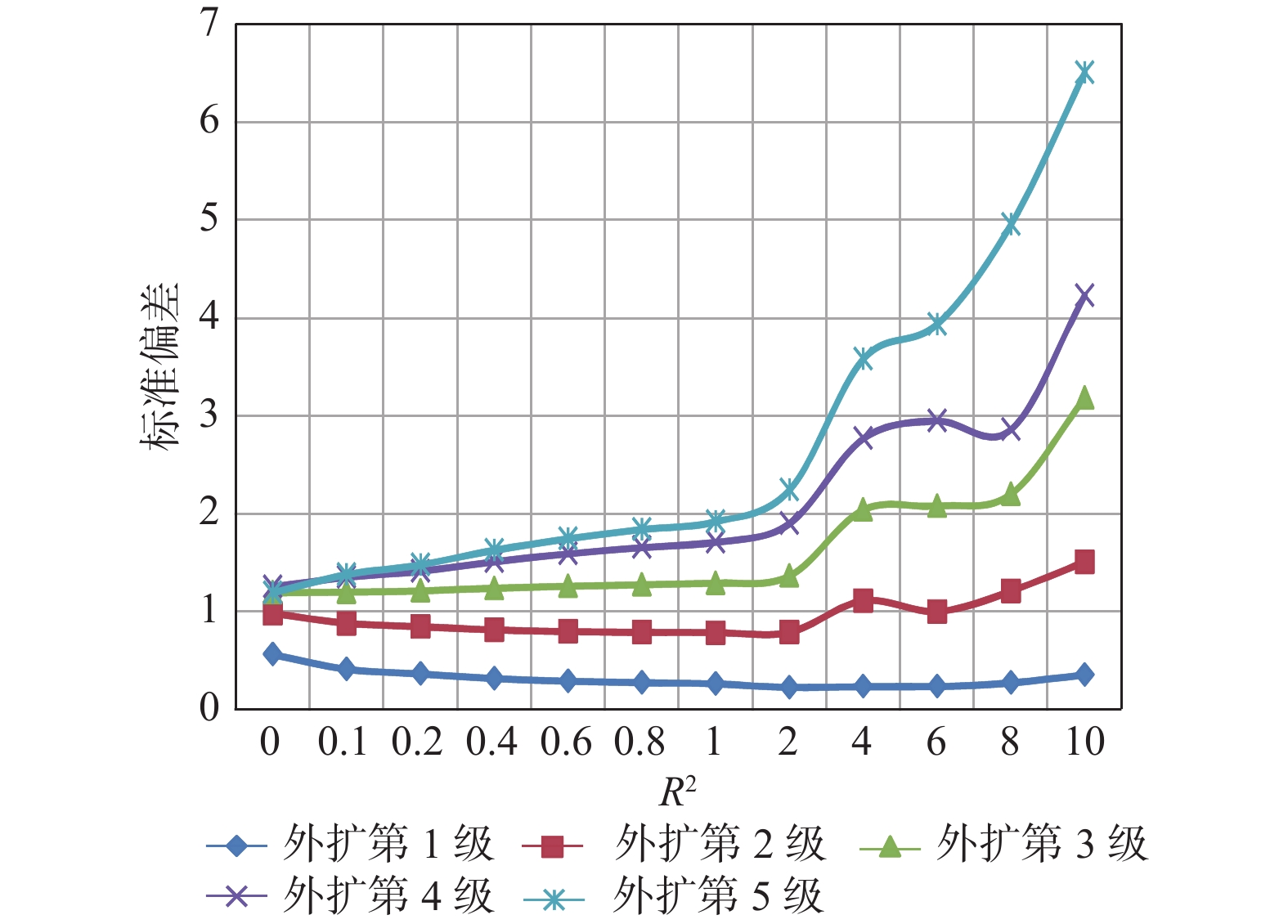
Table 4. Standard deviation results of different R²

R²	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
0	0.5584	0.9797	1.1909	1.2504	1.1892
0.1	0.4087	0.8779	1.1968	1.3479	1.3751
0.2	0.3608	0.8442	1.2099	1.4089	1.4746
0.4	0.3125	0.8105	1.2350	1.5078	1.6245
0.6	0.2876	0.7948	1.2562	1.5872	1.7404
0.8	0.2715	0.7869	1.2738	1.6525	1.8357
1	0.2593	0.7827	1.2883	1.7066	1.9171
2	0.2211	0.7878	1.3621	1.8961	2.2390
4	0.2324	1.1089	2.0364	2.7648	3.5768
6	0.2310	0.9977	2.0765	2.9441	3.9323
8	0.2708	1.2062	2.1974	2.8556	4.9508
10	0.3494	1.5053	3.1809	4.2262	6.5030

下载: 导出CSV

表 5 外扩第1级点的标准偏差结果

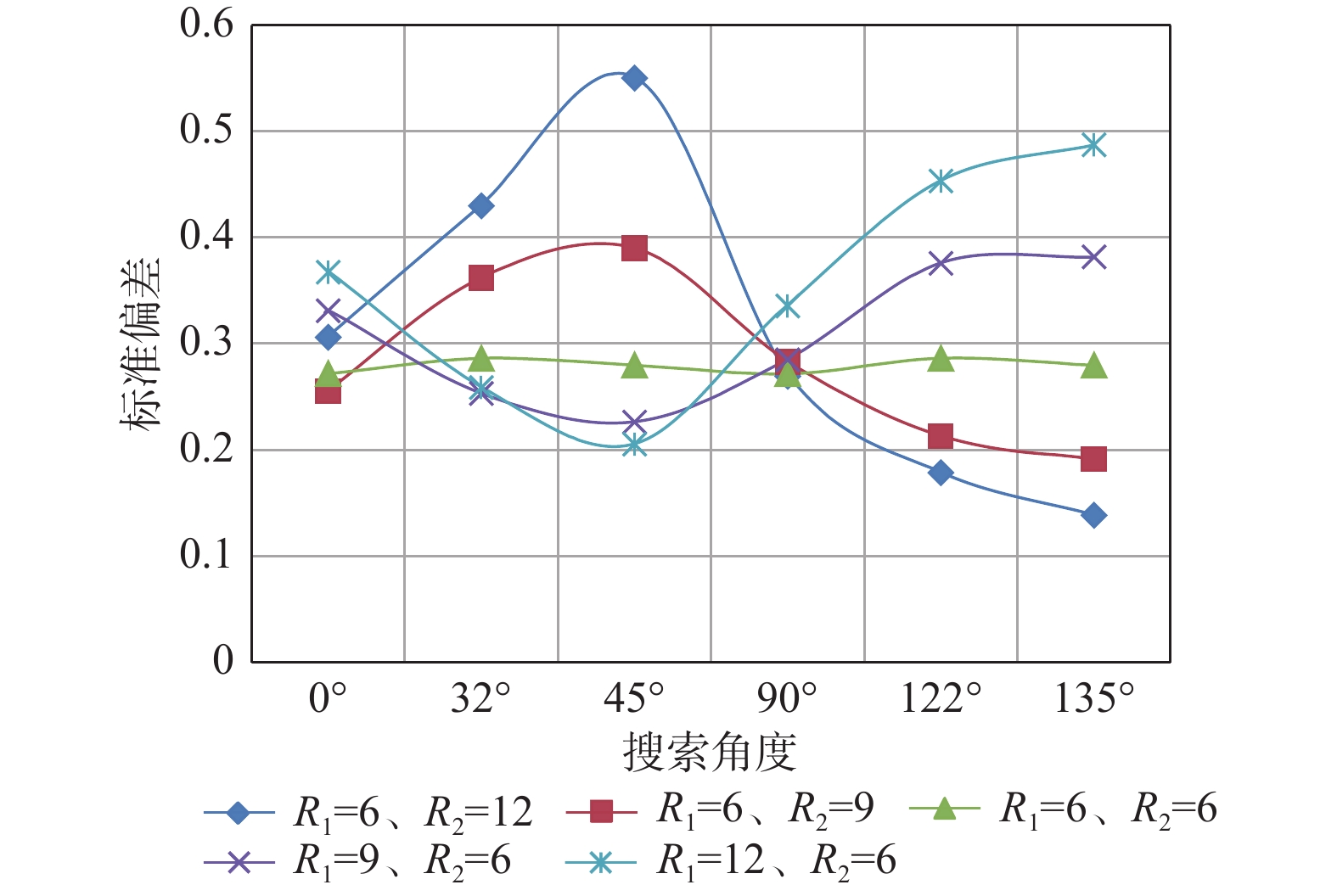
Table 5. Standard deviation results of the first level expanding points

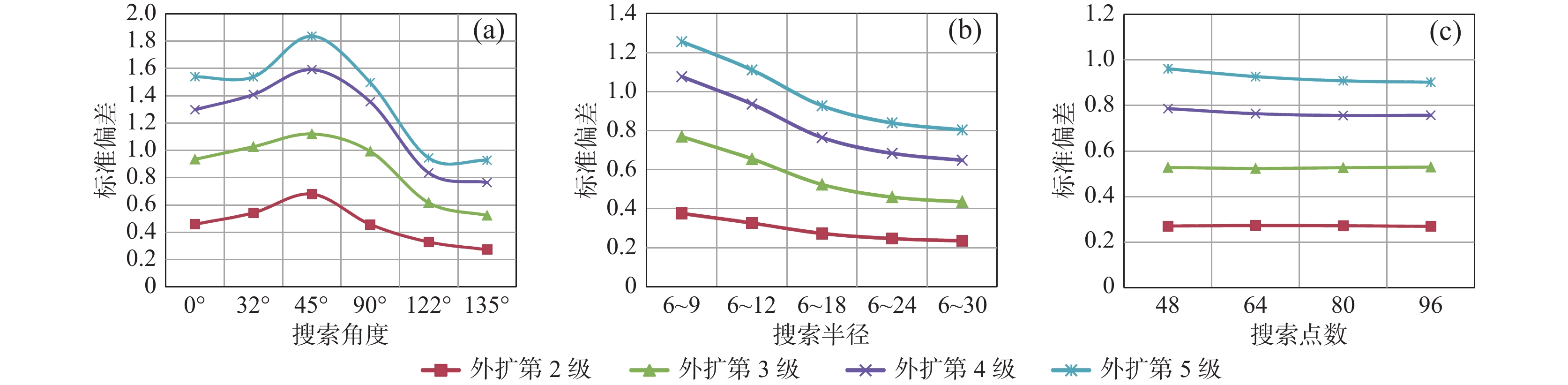
R₁～R₂		6～12	6～9	6～6	9～6	12～6
各向异性比率		0.5	0.667	1	1.5	2
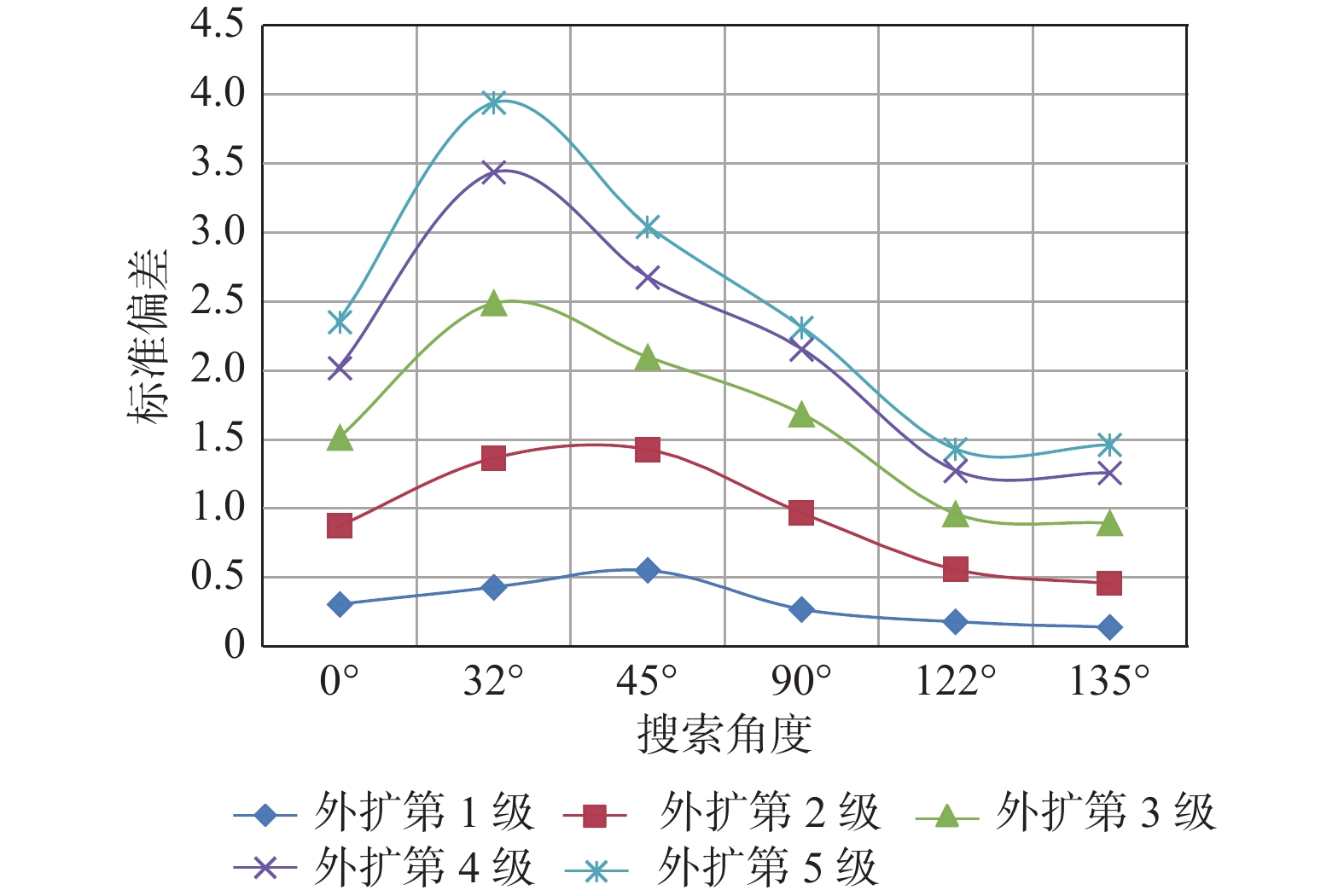
搜索角度= 各向异性角度	0°	0.3059	0.2550	0.2715	0.3310	0.3674
	32°	0.4297	0.3617	0.2861	0.2529	0.2586
	45°	0.5503	0.3898	0.2796	0.2263	0.2055
	90°	0.2694	0.2825	0.2715	0.2850	0.3355
	122°	0.1785	0.2127	0.2861	0.3758	0.4532
	135°	0.1385	0.1908	0.2796	0.3816	0.4872

下载: 导出CSV

表 6 半径R₁=6、R₂=12时外扩区标准偏差结果

Table 6. Standard deviation results of expanding area whenradius R₁=6 and R₂=12

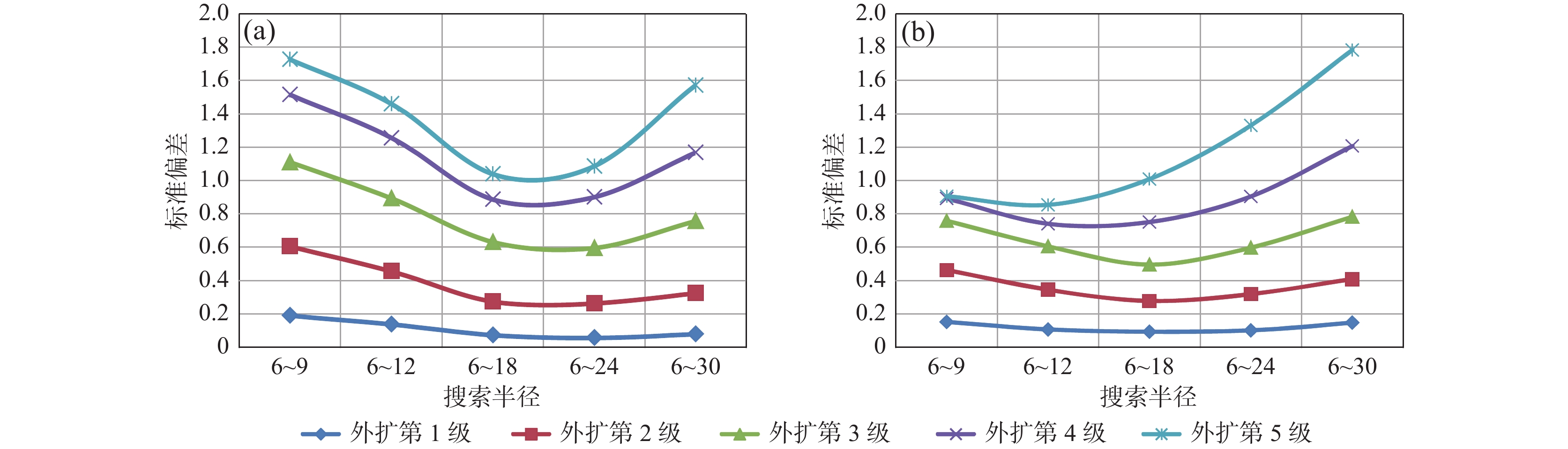
角度	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
0°	0.3059	0.8721	1.5104	2.0137	2.3485
32°	0.4297	1.3634	2.4833	3.4310	3.9359
45°	0.5503	1.4258	2.0933	2.6701	3.0374
90°	0.2694	0.9643	1.6802	2.1498	2.3067
122°	0.1785	0.5567	0.9594	1.2718	1.4273
135°	0.1385	0.4560	0.8938	1.2566	1.4601

下载: 导出CSV

表 7 不同搜索半径外扩区标准偏差结果

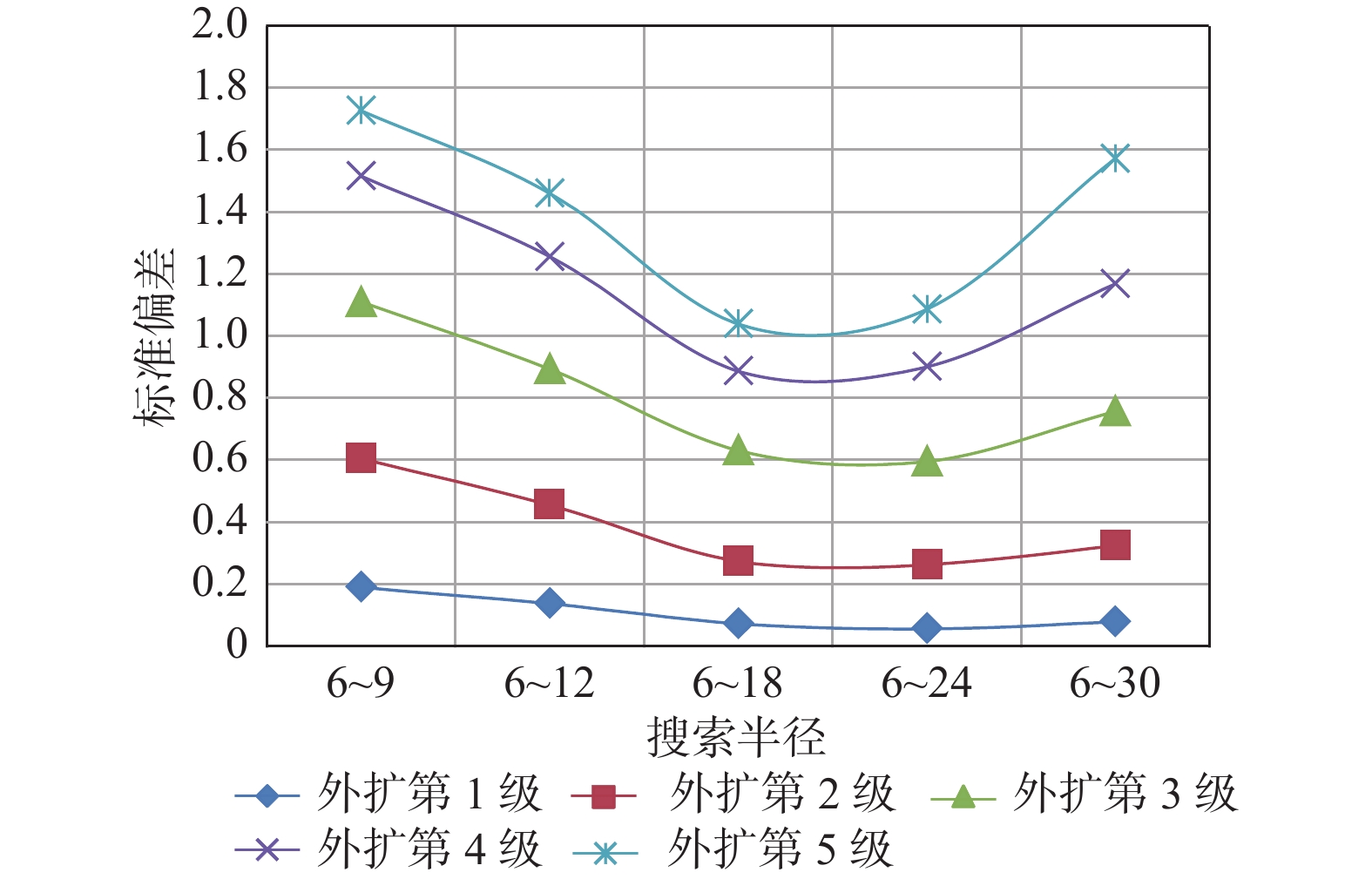
Table 7. Standard deviation results of expanding area with different search radius

半径 R₁～R₂	各向异性比率	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
6～9	0.667	0.1908	0.6063	1.1106	1.5160	1.7281
6～12	0.5	0.1385	0.4560	0.8938	1.2566	1.4601
6～18	0.333	0.0738	0.2743	0.6327	0.8879	1.0395
6～24	0.25	0.0574	0.2645	0.5969	0.9025	1.0871
6～30	0.2	0.0793	0.3245	0.7580	1.1690	1.5718

下载: 导出CSV

表 8 不同搜索点数外扩区标准偏差结果

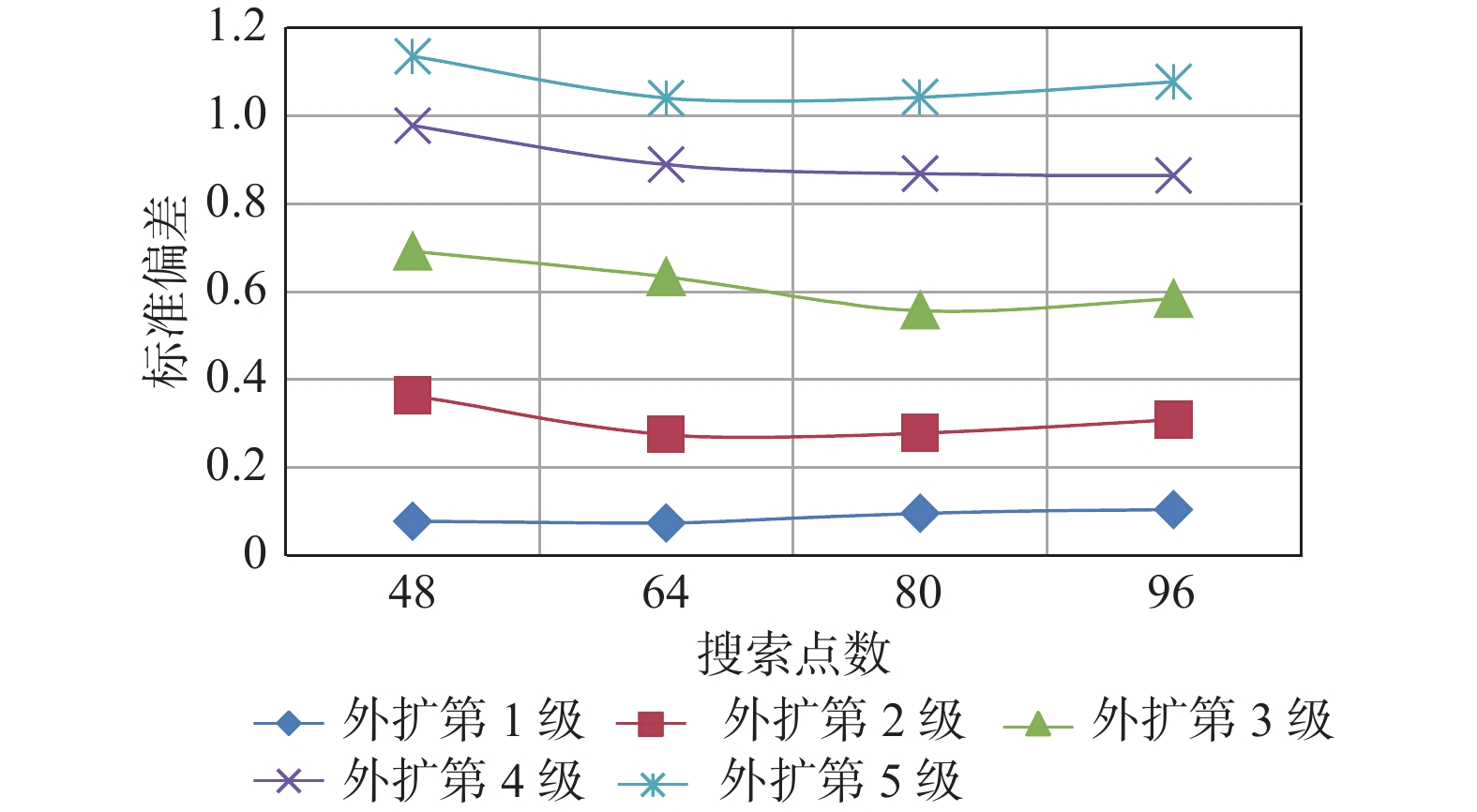
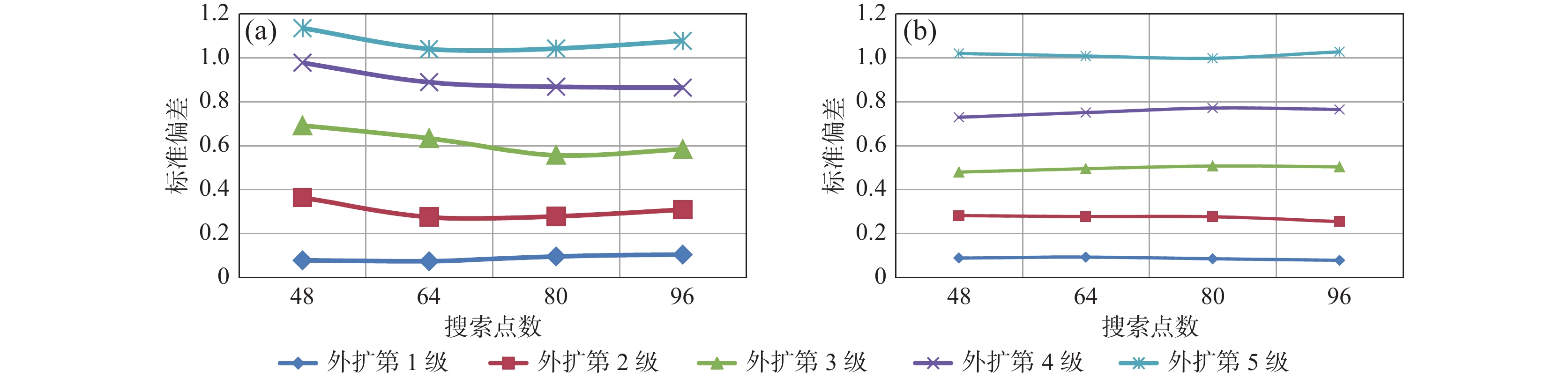
Table 8. Standard deviation results of expanding area with different search points

搜索点数	48	64	80	96
外扩第1级	0.0781	0.0738	0.0957	0.1037
外扩第2级	0.3628	0.2743	0.2779	0.3088
外扩第3级	0.6909	0.6327	0.5561	0.5834
外扩第4级	0.9767	0.8879	0.8673	0.8632
外扩第5级	1.1345	1.0395	1.0415	1.0765

下载: 导出CSV

表 9 仅考虑内部或外部最佳参数时外扩区标准偏差结果

Table 9. Standard deviation results of expanding area when only considered internal or external optimal parameters

参数选取	内部点	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
仅考虑外扩最佳参数时	0.01659	0.0738	0.2743	0.6327	0.8879	1.0395
仅考虑内插最佳参数时	0.01656	0.4235	1.7454	3.7984	6.0762	8.8219

下载: 导出CSV

表 10 不同搜索角度时新模型的扩边结果

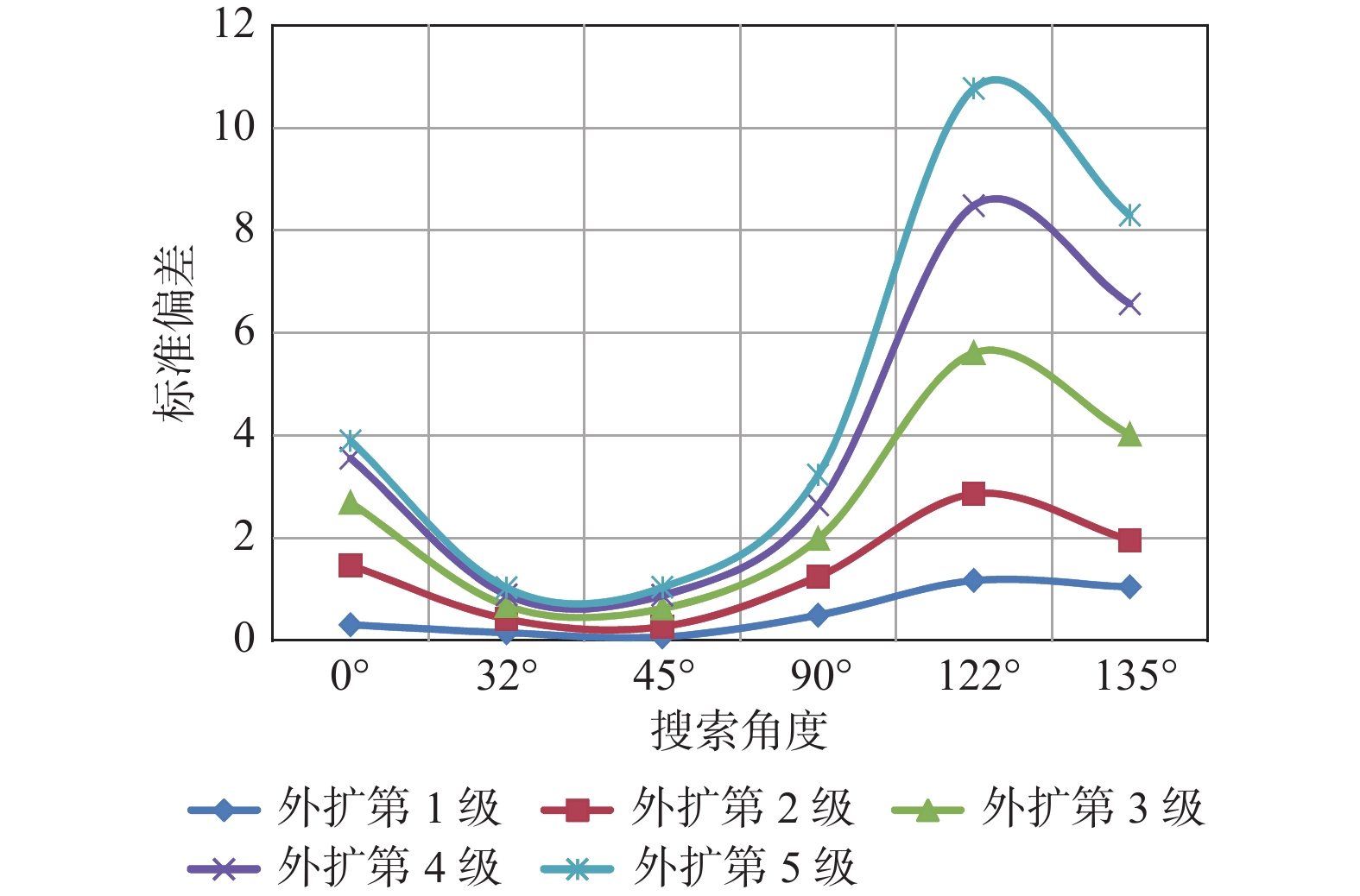
Table 10. Edge expanding results of new model with different search angles

搜索角度	0°	32°	45°	90°	122°	135°
外扩第1级	0.3109	0.1547	0.0738	0.4983	1.1727	1.0471
外扩第2级	1.4690	0.4251	0.2743	1.2504	2.8641	1.9599
外扩第3级	2.6924	0.6833	0.6327	1.9878	5.6132	4.0206
外扩第4级	3.5599	0.8962	0.8879	2.6471	8.4885	6.5704
外扩第5级	3.9009	1.0328	1.0395	3.2340	10.7697	8.3004

下载: 导出CSV

表 11 不同搜索角度时Y模型的扩边结果

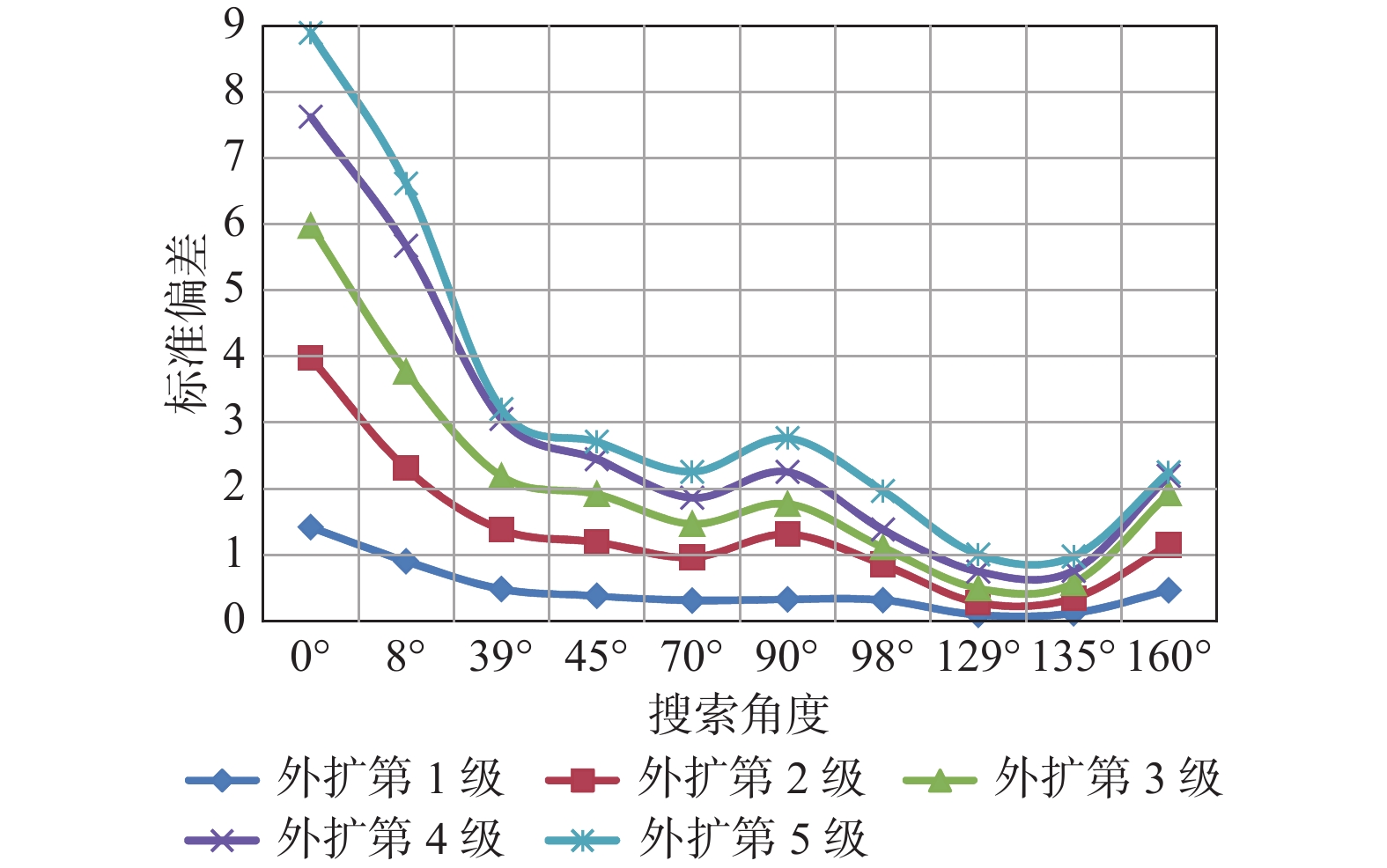
Table 11. Edge expanding results of Y model with different search angles

搜索角度	外扩第1级	外扩第2级	外扩第3级	外扩第4级	外扩第5级
0°	1.4208	3.9802	5.9726	7.6232	8.8935
8°	0.9059	2.3075	3.7689	5.6709	6.6191
39°	0.4838	1.3818	2.1895	3.0557	3.2056
45°	0.3833	1.1941	1.9197	2.4483	2.7107
70°	0.3108	0.9633	1.4703	1.8648	2.2582
90°	0.3309	1.3128	1.7726	2.2548	2.7663
98°	0.3186	0.8561	1.1129	1.3845	1.9681
129°	0.0935	0.2776	0.4958	0.7509	1.0083
135°	0.1206	0.3465	0.5737	0.7635	0.9791
160°	0.4661	1.1499	1.9294	2.1958	2.2504

下载: 导出CSV

参考文献(29)

白世彪, 王建, 常直杨. Surfer10地学计算机制图[M]. 北京: 科学出版社, 2012

BAI Shibiao, WANG Jian, CHANG Zhiyang. Surfer10 Geoscience Computer Mapping[M]. Beijing: Science Press, 2012.

陈欢欢,李星,丁文秀. Surfer8. 0等值线绘制中的十二种插值方法[J]. 工程地球物理学报,2007,4(1):52–57. doi: 10.3969/j.issn.1672-7940.2007.01.011

杜红悦,张浚哲,宫辉力. DEM产品数据质量分析研究与系统实现[J]. 测绘科学,2009,34(4):191–194.

段本春,徐世浙. 磁(重力)异常局部场与区域场分离处理中的扩边方法研究[J]. 物探化探计算技术,1997,19(4):298–304.

范威,江越潇,李寅,等. 湖北省江汉平原重点区地下水监测网优化研究[J]. 西北地质,2021,54(3):222–228. doi: 10.19751/j.cnki.61-1149/p.2021.03.019

李盼,戴前伟,吕宏安. 基于泛克里格方法的位场扩边处理[J]. 物探化探计算技术,2018,40(6):741–747. doi: 10.3969/j.issn.1001-1749.2018.06.08

刘芬,王万银,纪晓琳. 空间域和频率域平面位场延拓影响因素和稳定性分析[J]. 物探与化探,2019,43(2):320–328.

刘兆平,杨进,武炜. 地球物理数据网格化方法的选取[J]. 物探与化探,2010,34(1):93–97.

骆遥,吴美平. 位场向下延拓的最小曲率方法[J]. 地球物理学报,2016,59(1):240–251. doi: 10.6038/cjg20160120

马国庆,孟令顺,杜晓娟,等. 磁法数据处理中的扩边和优化中值滤波方法的研究[J]. 物探化探计算技术,2010,32(2):194–199. doi: 10.3969/j.issn.1001-1749.2010.02.016

毛小平,吴蓉元,曲赞. 频率域位场下延的振荡机制及消除方法[J]. 石油地球物理勘探,1998,33(2):230–237. doi: 10.13810/j.cnki.issn.1000-7210.1998.02.011

庞振兴,张传定,叶修松. Surfer8. 0在重力异常数据格网化中的应用[J]. 海洋测绘,2008,28(1):43–51. doi: 10.3969/j.issn.1671-3044.2008.01.012

孙文,吴晓平,王庆宾,等. 高精度重力数据格网化方法比较[J]. 大地测量与地球动力学,2015,35(2):342–345. doi: 10.14075/j.jgg.2015.02.037

王万银,邱之云,刘金兰,等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展,2009,24(4):1327–1338. doi: 10.3969/j.issn.1004-2903.2009.04.022

王万银,邱之云. 一种稳定的位场数据最小曲率网格化方法研究[J]. 地球物理学进展,2011,26(6):2003–2010. doi: 10.3969/j.issn.1004-2903.2011.06.014

王兆国,程顺有,刘财. 地球物理勘探中几种二维插值方法的误差分析[J]. 吉林大学学报(地球科学版),2013,43(6):1997–2004. doi: 10.13278/j.cnki.jjuese.2013.06.040

吴洪彬. 多项式拟合扩边方法[J]. 黑龙江科技信息,2012,16:8.

吴太旗,黄谟涛,欧阳永忠,等. 高精度海洋重力异常格网插值技术研究[J]. 测绘科学,2008,33(5):70–72. doi: 10.3771/j.issn.1009-2307.2008.05.024

吴卫国. Surfer网格化与白化处理在数据扩边中的应用——以1: 5万水系沉积物测量成图为例[J]. 物探与化探,2015,39(3):602–605.

肖锋,孟令顺,吴燕刚. 在波数域计算一维重磁异常导数的Matlab语言算法[J]. 物探与化探,2008,32(3):316–320.

许海红,韩小锋,袁炳强,等. 基于径向基函数的1: 5万规则分布重力数据插值参数优选[J]. 物探与化探,2021,45(6):1539–1552.

许海红,卢进才,李玉宏,等. 基于Surfer的1: 50000规则测网重力数据网格化方法选取——以银额盆地赛汉陶来区块重力资料为例[J]. 地球物理学进展,2015,30(6):2566–2573.

徐如刚,梁霄,孙鸿博,等. 扩边尺度对重力异常分层分离处理的影响——以插值切割法为例[J]. 大地测量与地球动力学,2021,41(3):221–228. doi: 10.14075/j.jgg.2021.03.001

姚长利,管志宁,高德章,等. 低纬度磁异常化极方法——压制因子法[J]. 地球物理学报,2003,46(5):690–696. doi: 10.3321/j.issn:0001-5733.2003.05.017

曾小牛,李夕海,侯维君,等. 基于凸集投影的重力同时填充扩边和去噪方法[J]. 石油地球物理勘探,2020,55(1):197–205. doi: 10.13810/j.cnki.issn.1000-7210.2020.01.023

曾小牛,李夕海,刘继昊,等. 基于凸集投影的重力数据扩充下延一体化方法[J]. 石油地球物理勘探,2019,54(5):1166–1173. doi: 10.13810/j.cnki.issn.1000-7210.2019.05.025

张锦明,游雄,万刚. 径向基函数算法中插值参数对DEM精度的影响[J]. 武汉大学学报·信息科学版,2013,38(5):608–612. doi: 10.13203/j.whugis2013.05.013

张志厚,徐世浙,余海龙,等. 位场向下延拓的迭代法的扩边方法[J]. 浙江大学学报(工学版),2013,47(5):918–924.

中华人民共和国国土资源部. DZ/T 0004-2015, 重力调查技术规范(1: 50000)[S]. 北京: 地质出版社, 2015

Ministry of Land and Resources of the People’s Republic of China. DZ/T 0004-2015, The technical specification for gravity survey (1: 50000)[S]. Beijing: Geological Publishing House, 2015.

施引文献

资源附件(0)

访问统计

图(21)

表(11)

计量

文章访问数: 648
PDF下载数: 47
施引文献: 0

基于逐级迭代插值的重力数据扩边方法研究

1. 中国地质调查局西安地质调查中心/西北地质科技创新中心，陕西 西安 710054 2. 西安石油大学地球科学与工程学院，陕西 西安 710065 3. 陕西省矿产地质调查中心，陕西 西安 710068

作者简介: 许海红（1984−），男，高级工程师，主要从事油气资源勘查研究工作。E–mail：honghaibeibei@163.com

通讯作者: 王宝文（1984−），男，高级工程师，主要从事油气资源潜力评价工作。E–mail：wang_bw@163.com

Research on the Method of Gravity Data Edge Expanding Based on Step By Step Iterative Interpolation

Corresponding author: WANG Baowen, wang_bw@163.com

计量

出版历程

目录

1.
中国地质调查局西安地质调查中心/西北地质科技创新中心，陕西西安　710054

2.
西安石油大学地球科学与工程学院，陕西西安　710065

3.
陕西省矿产地质调查中心，陕西西安　710068