Research on experimental tests and prediction models of thermal conductivity of freezing-thawing soil in the Kunlun Mountains
-
摘要:
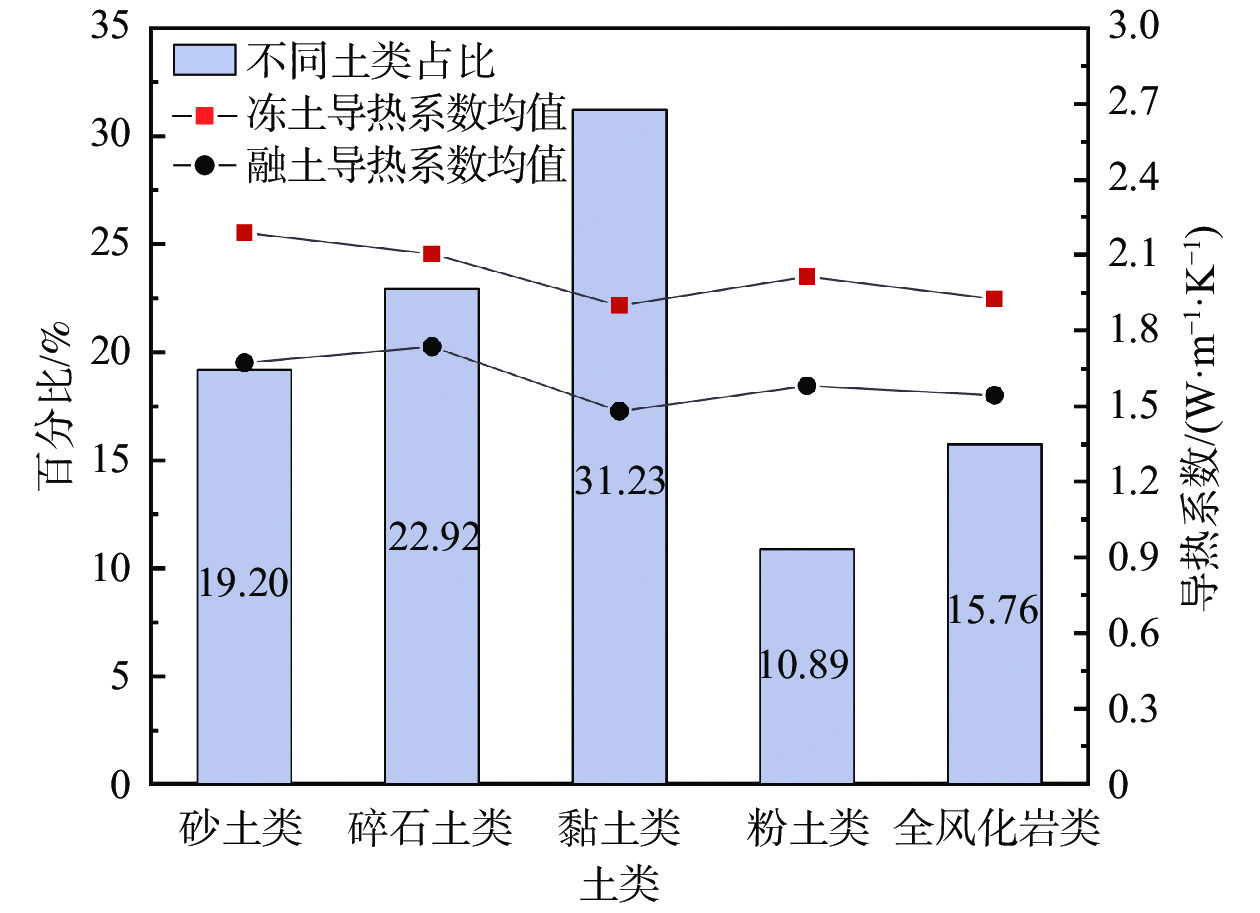
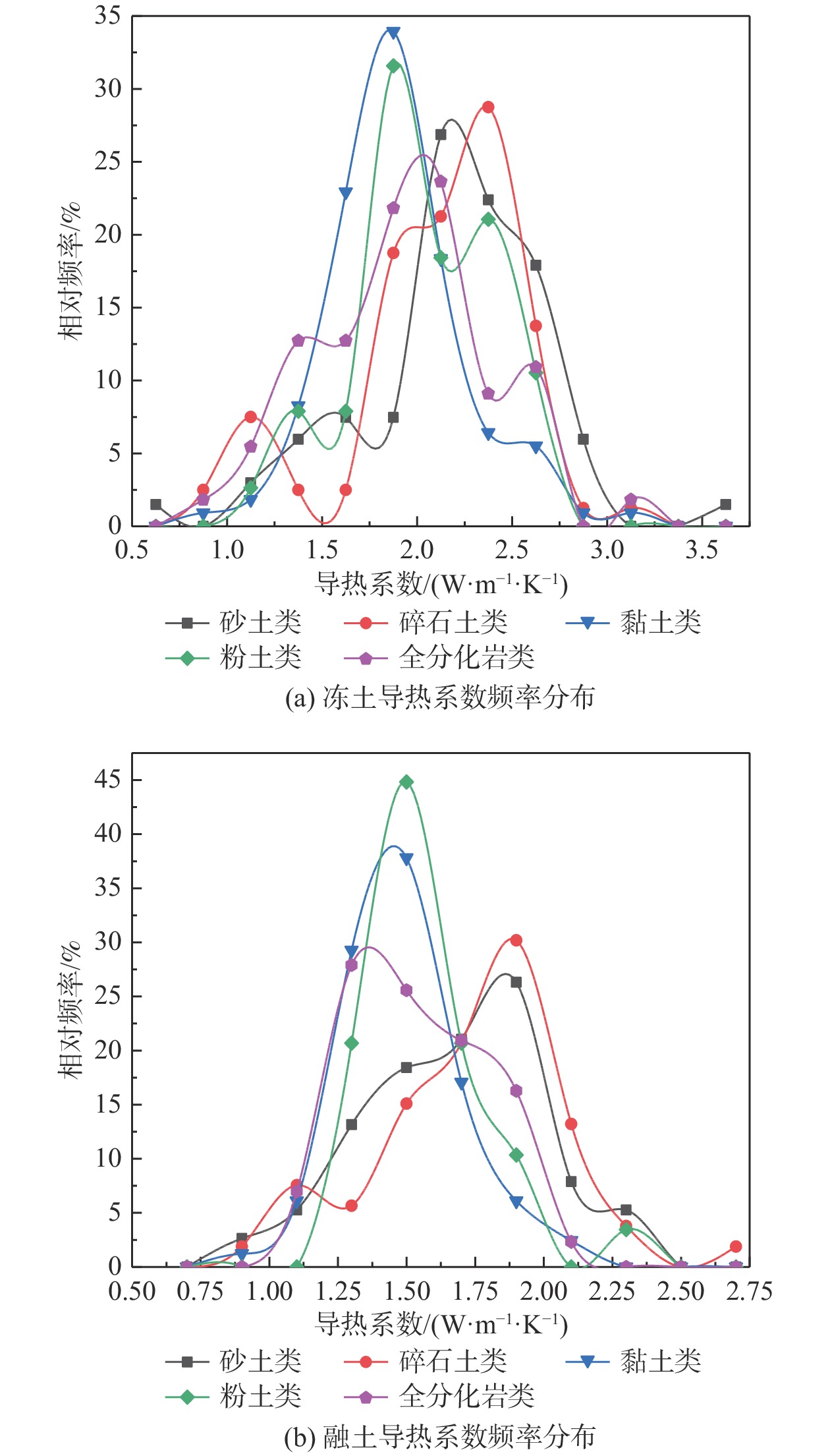
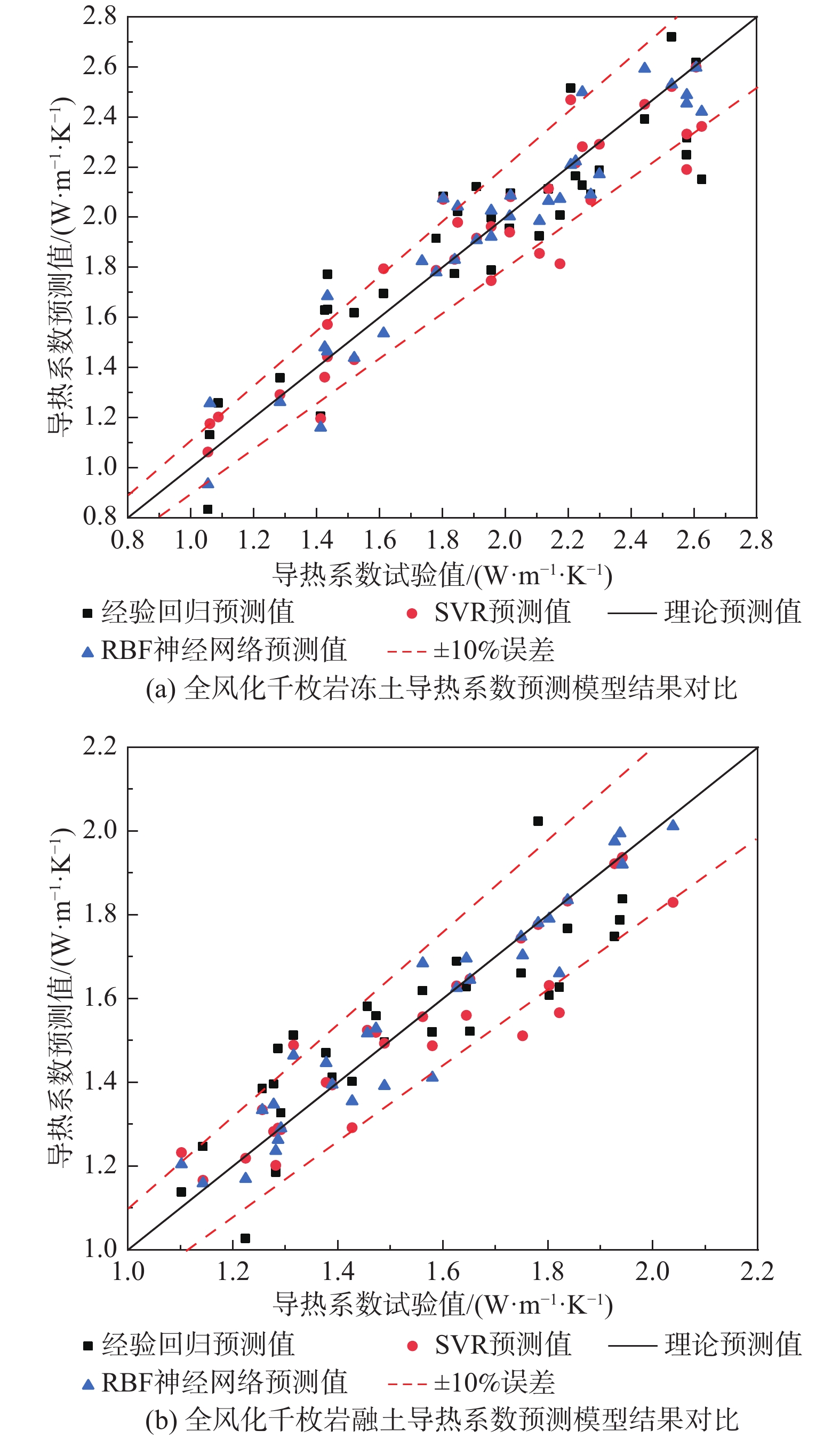
为探究青藏高原工程走廊带昆仑山地区冻融土导热系数基本特征,采用瞬态平面热源法对钻取的349组冻土试样和245组融土试样导热系数进行了测试,分析了五类土导热系数分布特征及天然含水率、干密度与导热系数的偏相关性,并以两者为变量因素建立了经验公式拟合、支持向量回归(SVR)和径向基(RBF)神经网络导热系数预测模型。结果表明:冻融土导热系数整体均呈粗颗粒土大于细颗粒土特征,且冻土和融土导热系数随土性分布规律存在差异;天然含水率、干密度与导热系数均呈正相关性,不同土类偏相关性结果差异明显,典型土导热系数二元经验回归方程表现为非线性拟合结果。对比三种预测模型下各典型土冻融土导热系数预测结果,全风化千枚岩、角砾及砾砂三种预测模型效果整体较佳,粉土的SVR及RBF神经网络预测精度较好;融土导热系数预测效果整体略优于冻土,SVR及RBF神经网络模型下角砾、粉土及全风化千枚岩融土导热系数预测精度较高。综合导热系数模型预测效果和误差结果分析可得,SVR和RBF神经网络模型预测效果显著优于经验方程拟合,后者针对部分土性拟合效果相对较好,可满足一般工程估算需求;SVR和RBF神经网络预测模型针对不同土性导热系数预测效果呈差异性变化,整体预测效果相当,且预测精度更高、应用土性范围更广。
Abstract:In order to explore the basic laws of freezing and thawing soil in the Qinghai-Xizang Engineering Corridor in the Kunlun Mountains area, the coefficient of thermal conductivity of 349 groups of drilling frozen soil samples and 245 groups of thawing soil samples is tested by the transient plane heat source method. The characteristics of five kinds of soil thermal conductivity distribution and natural moisture content, dry density and the partial correlation coefficient of thermal conductivity are analyzed, and the experience for both variables in fitting formula, support vector regression (SVR) and radial basis (RBF) neural network prediction model of thermal conductivity are established. The results show that the thermal conductivity of freezing-thawing soil is larger than that of fine-grained soil, and the thermal conductivity of freezing-thawing soil varies with the distribution of soil properties. Natural moisture content and dry density are positively correlated with thermal conductivity, and the partial correlation results of different soil types are significantly different. The binary empirical regression equation of typical soil thermal conductivity is shown as a nonlinear fitting result. The results of thermal conductivity prediction of the typical soil and freezing-thawing soil under three prediction models show that the prediction effect of fully weathered phyllite, breccia and gravel sand is better, and the prediction accuracy of SVR and RBF neural network of silty soil is also better. On the whole, the prediction effect of thermal conductivity on thawed soil is slightly better than that of frozen soil, and the prediction accuracy of thermal conductivity of breccias, silty soil and fully weathered meltwater is higher under the SVR and RBF neural network models. The prediction results and error analysis of the three thermal conductivity models show that the prediction results of the SVR and RBF neural network models are significantly better than that of the empirical fitting equation method. The prediction effect of SVR and RBF neural network prediction models varies with different soil thermal conductivities, and the overall prediction effect is similar, with higher prediction accuracy and wider range of soil application.
-
Key words:
- Kunlun Mountains area /
- thermal conductivity /
- partial correlation analysis /
- SVR /
- RBF neural network /
- frozen soil
-

-
表 1 土样基本物性参数
Table 1. Basic physical parameters of the soil samples
土性 含水率/% 干密度/(g·cm−3) 分布范围 均值 分布范围 均值 砂土类 2.6~83.0 22.2 0.880~2.297 1.665 碎石土类 2.9~118.0 20.9 0.688~2.280 1.705 黏土类 6.9~148.2 30.1 0.612~2.046 1.551 粉土类 4.5~99.3 27.5 0.813~1.977 1.560 全风化岩类 1.6~75.4 18.3 0.810~2.290 1.760 表 2 Hot Disk测试仪参数
Table 2. Hot Disk tester parameters
传感器 导热系数范围/(W·m−1·K−1) 温度范围/K 精度/% 重复性/% Kapton 0.005~20 10~1000 ±3 ±1 表 3 导热系数与含水率、干密度偏相关分析
Table 3. Partial correlation analysis of thermal conductivity with moisture content and dry density
土性 变量 融土 冻土 变量 融土 冻土 相关性 显著性 相关性 显著性 相关性 显著性 相关性 显著性 砂土类 含水率 0.508 0.001 0.282 0.022 干密度 0.545 0.000 0.199 0.109 导热系数 导热系数 碎石土类 含水率 0.700 0.000 0.339 0.002 干密度 0.566 0.000 0.246 0.029 导热系数 导热系数 黏土类 含水率 0.186 0.096 0.232 0.016 干密度 0.325 0.003 0.236 0.014 导热系数 导热系数 粉土类 含水率 0.004 0.986 0.215 0.201 干密度 0.203 0.301 0.206 0.221 导热系数 导热系数 全风化岩类 含水率 0.571 0.000 0.207 0.132 干密度 0.359 0.019 0.061 0.664 导热系数 导热系数 表 4 各种土二元经验回归拟合结果
Table 4. Binary empirical regression fitting results for all kinds of soil
土类 导热系数经验回归公式 砾砂 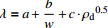
角砾 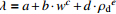
粉质黏土 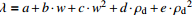
粉土 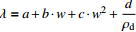
全风化千枚岩 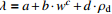
注:式中w为含水率,ρd为干密度,a、b、c、d、e为拟合参数。 表 5 各种土二元经验回归公式参数
Table 5. Binary empirical regression formula parameters for all kinds of soil
土类 a b c d e 砾砂 融土 −1.82 −2.59 2.83 − − 冻土 0.97 −5.03 1.36 − − 角砾 融土 −41.50 4.27×101 1.50×10−2 −3.72 −2.11 冻土 −503.54 5.01×102 2.00×10−3 1.43 1.04 粉质黏土 融土 −1.85 −3.20×10−2 1.00×10−3 3.83 −1.01 冻土 0.24 1.70×10−2 0 0.58 0.15 粉土 融土 0.42 2.90×10−1 −1.70×10−2 −0.41 − 冻土 1.35 8.70×10−2 −2.00×10−3 −0.67 − 全风化千枚岩 融土 −2.70 7.80×10−1 3.40×10−1 1.32 − 冻土 −343.66 3.40×102 3.00×10−3 1.80 − 表 6 SVR预测模型网格搜索优选参数
Table 6. SVR optimal parameters obtained from grid search of the prediction model
土性 砾砂 角砾 粉质黏土 粉土 全风化千枚岩 融土 冻土 融土 冻土 融土 冻土 融土 冻土 融土 冻土 惩罚参数(C) 0.25 2.00 5.66 22.63 1.41 0.09 1.00 90.51 1.00 4.00 核函数超参数(g) 3.28×104 32.00 1.41 1.41 4.00 128.00 11.31 16.00 16.00 4.00 表 7 经验公式与机器学习回归模型预测结果
Table 7. Forecast results of the empirical formula and regression model of machine learning
土性 砾砂 角砾 粉质黏土 粉土 全风化千枚岩 融土 冻土 融土 冻土 融土 冻土 融土 冻土 融土 冻土 经验公式 R2 0.59 0.60 0.68 0.58 0.21 0.12 0.59 0.34 0.75 0.83 MSE 0.05 0.08 0.03 0.08 0.03 0.09 0.01 0.07 0.02 0.04 MAPE/% 10.50 11.54 7.78 11.28 9.41 12.19 6.32 10.78 7.14 8.92 相对误差10%内 50.00 52.78 70.97 52.00 59.10 47.73 77.78 60.00 75.00 63.64 SVR R2 0.79 0.85 0.86 0.73 0.51 0.25 0.91 0.85 0.87 0.88 MSE 0.04 0.04 0.01 0.06 0.02 0.07 0.00 0.02 0.01 0.03 MAPE/% 7.55 5.05 4.52 8.40 6.58 10.40 2.42 3.55 4.07 6.03 相对误差10%内 70.00 83.33 87.10 66.00 75.76 56.82 89.66 85.71 83.33 69.70 RBF R2 0.72 0.77 0.98 0.81 0.50 0.43 0.93 0.72 0.92 0.91 MSE 0.03 0.06 0.00 0.04 0.02 0.06 0.00 0.03 0.01 0.02 MAPE/% 7.99 6.65 1.24 7.71 7.51 10.00 2.49 6.35 3.70 5.60 相对误差10%内 65.00 72.22 96.77 68.00 71.21 56.82 96.55 74.29 93.33 78.79 -
[1] JIN Huijun, ZHAO Lin, WANG Shaoling, et al. Thermal regimes and degradation modes of permafrost along the Qinghai-Xizang Highway[J]. Science in China(Series D: Earth Sciences),2006 49(11):1170 − 1183.
[2] PENG Hui, MA Wei, MU Yanhu, et al. Degradation characteristics of permafrost under the effect of climate warming and engineering disturbance along the Qinghai–Xizang Highway[J]. Natural Hazards,2015,75(3):2589 − 2605. doi: 10.1007/s11069-014-1444-5
[3] 董元宏, 彭惠, 罗滔, 等. 气候变暖背景下拟建青藏高速公路沿线典型区段多年冻土未来50年退化特征[J]. 灾害学,2019,34(增刊1):20 − 25. [DONG Yuanhong, PENG Hui, LUO Tao, et al. Degradation characteristics of the permafrost at typical sites along Qinghai-Xizang expressway in the next 50 years under climate warming background[J]. Journal of Catastrophology,2019,34(Sup1):20 − 25. (in Chinese with English abstract)
[4] 徐敩祖, 陶兆祥, 傅素兰. 典型融冻土的热学性质[C]//中国科学院兰州冰川冻土研究所集刊第2号. 北京: 科学出版社, 1981.
XU Xiaozu, TAO Zhaoxiang, FU Sulan. Thermal properties of typical unfrozen and frozen soil[C]//Memoirs of Lanzhou Institute of Glaciology and Crypedology, Academia Sinica(Vol.2). Beijing: Science Press, 1981. (in Chinese)
[5] 肖忠华. 上海软土二次冻融土工程性质试验研究[D]. 上海: 同济大学, 2007.
XIAO Zhonghua. Experimental investigation on engineering properties of Shanghai soft soils under secondary freeze-thaw action[D]. Shanghai: Tongji University, 2007. (in Chinese with English abstract)
[6] 尹飞. 冻土导热系数的仪器研制和稳态法模拟试验研究[D]. 长春: 吉林大学, 2008.
YIN Fei. The instrumental development of thermal conductivity of frozen ground and the research on the steady-state method simulation test[D]. Changchun: Jilin University, 2008. (in Chinese with English abstract)
[7] 王伟. 冻土传热性质试验研究[D].长春: 吉林大学, 2010.
WANG Wei. The experiments research on thermal conductivity of frozen soil[D]. Changchun: Jilin University, 2010.(in Chinese with English abstract)
[8] 阮传侠, 冯树友, 牟双喜, 等. 天津地区地层热物性特征及影响因素分析[J]. 水文地质工程地质,2017,44(5):158 − 163. [RUAN Chuanxia, FENG Shuyou, MOU Shuangxi, et al. An analysis of the characteristics of thermal physical properties and their influencing factors in the Tianjin area[J]. Hydrogeology & Engineering Geology,2017,44(5):158 − 163. (in Chinese with English abstract)
[9] 李思齐, 杨平, 赵方舟. 砾石地层冻土热物理特性研究[J]. 水文地质工程地质,2008,45(6):122 − 126. [LI Siqi, YANG Ping, ZHAO Fangzhou. A study of the thermal physical properties of frozen soil in gravel layers[J]. Hydrogeology & Engineering Geology,2008,45(6):122 − 126. (in Chinese with English abstract)
[10] 姜雄. 多年冻土区高温冻土导热系数试验研究[D]. 徐州: 中国矿业大学, 2015.
JIANG Xiong. Experimental study on thermal conductivity for warm frozen soils in permafrost regions[D].Xuzhou: China University of Mining and Technology, 2015.(in Chinese with English abstract)
[11] 张婷, 杨平. 不同因素对浅表土导热系数影响的试验研究[J]. 地下空间与工程学报,2012,8(6):1233 − 1238. [ZHANG Ting, YANG Ping. Effect of different factors on the heat conduction coefficient of shallow top soil[J]. Chinese Journal of Underground Space and Engineering,2012,8(6):1233 − 1238. (in Chinese with English abstract)
[12] 何玉洁, 宜树华, 郭新磊. 青藏高原含砂砾石土壤导热率实验研究[J]. 冰川冻土,2017,39(2):343 − 350. [HE Yujie, YI Shuhua, GUO Xinlei. Experimental study on thermal conductivity of soil with gravel on the Qinghai-Xizang Plateau[J]. Journal of Glaciology and Geocryology,2017,39(2):343 − 350. (in Chinese with English abstract)
[13] 温智, 盛煜, 马巍, 等. 青藏高原北麓河地区原状多年冻土导热系数的试验研究[J]. 冰川冻土,2005 27(2):182 − 187. [WEN Zhi, SHENG Yu, MA Wei, et al. Experimental studies of thermal conductivity of undisturbed permafrost at Beiluhe testing site on the Xizang plateau[J]. Journal of Glaciology and Geocryology,2005 27(2):182 − 187. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-0240.2005.02.005
[14] JOHANSEN O. Thermal conductivity of soils[D]. Norway: Trondheim University, 1975.
[15] CÔTÉ J, KONRAD J M. A generalized thermal conductivity model for soils and construction materials[J]. Canadian Geotechnical Journal,2005,42(2):443 − 458. doi: 10.1139/t04-106
[16] ZHU Ming. Modeling and simulation of frost heave in frost-susceptible soils[D]. Ann Arbor: University of Michigan, 2006.
[17] 罗斯琼, 吕世华, 张宇, 等. 青藏高原中部土壤热传导率参数化方案的确立及在数值模式中的应用[J]. 地球物理学报,2009,52(4). [LUO Siqiong, LV Shihua, ZHANG Yu, et al. Soil thermal conductivity parameterization establishment and application in numerical model of central Xizang Plateau[J]. Chinese Journal of Geophysics,2009,52(4). (in Chinese with English abstract) doi: 10.3969/j.issn.0001-5733.2009.04.030
[18] 李顺群, 陈之祥, 夏锦红, 等. 冻土导热系数的聚合模型研究及试验验证[J]. 中国公路学报,2018,31(8):39 − 46. [LI Shunqun, CHEN Zhixiang, XIA Jinhong, et al. Aggregation model research and experimental verification of frozen soil thermal conductivity[J]. China Journal of Highway and Transport,2018,31(8):39 − 46. (in Chinese with English abstract)
[19] 戚家忠, 储党生, 韩彦智. 祁东矿人工冻土物理力学性能试验研究[J]. 淮南工业学院学报,1999 19(3):3 − 5. [QI Jiazhong, CHU Dangsheng, HAN Yanzhi. Experimental study on physical and mechanical properties of artificial frozen soil in Qidong Mine[J]. Journal of Huainan Institute of Technology(Natural Science),1999 19(3):3 − 5. (in Chinese with English abstract)
[20] 洪涛, 梁四海, 孙禹, 等. 黄河源区多年冻土热传导系数影响因素分析及其在活动层厚度模拟中的应用[J]. 冰川冻土,2013,35(4):824 − 833. [HON G Tao, LIANG Sihai, SUN Yu, et al. Analyzing the factors that impact on the heat conductivity coefficient and applying them to simulate the depth of permafrost active layer in the headwaters of the Yellow River[J]. Journal of Glaciology and Geocryology,2013,35(4):824 − 833. (in Chinese with English abstract)
[21] 何发祥, 黄英. 用BP网络求解土体的导热系数[J]. 岩土力学,2000, 21(1):84 − 87. [HE Faxiang, HUANG Ying. Solution of thermal conduction coefficient from BP network[J]. Rock and Soil Mechanics,2000, 21(1):84 − 87. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2000.01.021
[22] 袁玉倩, 薛桂香, 孙春华, 等. 基于BP神经网络的土壤热导率预测算法研究[J]. 河北工业大学学报,2015,44(6):39 − 44. [YUAN Yuqian, XUE Guixiang, SUN Chunhua, et al. A study of soil thermal conductivity prediction algorithm based on BP neural network[J]. Journal of Hebei University of Technology,2015,44(6):39 − 44. (in Chinese with English abstract)
[23] BANG H T, YOON S, JEON H. Application of machine learning methods to predict a thermal conductivity model for compacted bentonite[J]. Annals of Nuclear Energy,2020,142:107395. doi: 10.1016/j.anucene.2020.107395
[24] 周幼吾, 郭东信, 邱国庆.中国冻土[M]. 北京: 科学出版社, 2010.
ZHOU Youwu, GUO Dongxin, QIU Guoqing. Geocryology in China[M]. Beijing: Science Press, 2010. (in Chinese)
[25] LUTS J, OJEDA F, PLAS R V D, et al. A tutorial on support vector machine-based methods for classification problems in chemometrics[J]. Analytica Chimica Acta,2010,665(2):129 − 145. doi: 10.1016/j.aca.2010.03.030
[26] LIU Y, PARHI K K. Computing RBF Kernel for SVM Classification Using Stochastic Logic[C]//IEEE International Workshop on Signal Processing Systems. IEEE, 2016: 327−332.
[27] 周维华. RBF神经网络隐层结构与参数优化研究[D].上海: 华东理工大学, 2014.
ZHOU Weihua. Optimization study of the hidden structure and parameter in the RBF neural networks[D]. Shanghai: East China University of Science and Technology, 2014. (in Chinese with English abstract)
-




 下载:
下载: