基于非均质系数的裂隙岩体表征单元体研究

王晓明; 杜玉芳; 梁旭黎

doi:10.16030/j.cnki.issn.1000-3665.202007029

基于非均质系数的裂隙岩体表征单元体研究

1.
河北地质大学城市地质与工程学院，河北石家庄　050031

2.
河北地质大学河北省高校生态环境地质应用技术研发中心，河北石家庄　050031

基金项目: 国家自然科学基金项目（41902298）；河北省自然科学基金项目（D2019403151）；河北省教育厅在读研究生创新能力培养资助项目（CXZZSS2021124）；河北地质大学博士科研启动基金项目（1714023）

详细信息

作者简介: 王晓明（1984-），男，高级工程师，博士，从事岩体工程地质教学与研究。E-mail： wangxiaoming@hgu.edu.cn

通讯作者: 梁旭黎（1981-），女，讲师，硕士，主要从事岩石力学教学和研究工作。E-mail： liangxuli@foxmail.com

中图分类号: TU452

收稿日期: 2020-07-13

修回日期: 2020-10-12

刊出日期: 2021-03-15

Investigation of the representative elementary volume of fractured rock mass using the homogeneity index

1.
School of Urban Geology and Engineering, Hebei GEO University, Shijiazhuang, Hebei　050031, China

2.
Hebei Center for Ecological and Environmental Geology Research, Hebei GEO University, Shijiazhuang, Hebei　050031, China

More Information

Corresponding author: LIANG Xuli, liangxuli@foxmail.com

Received Date: 13 July 2020

Revised Date: 12 October 2020

Publish Date: 15 March 2021

摘要

摘要:
表征单元体（REV）是岩体力学中的一个基础性概念，其存在性是确定岩体等效参数和应用连续介质方法进行研究的前提条件。为综合反映裂隙大小、产状和密度对岩体REV的影响，本文提出采用岩体非均质系数HI来确定岩体的REV。首先，详细介绍了非均质系数的概念和含义。利用General Block软件建立了中等间距-中等延展性（MS1-MP1）裂隙的网络模型，并完成20次随机实现。从各模型中选取10个不同尺寸的岩体模型计算非均质系数，结果表明：非均质系数具有明显的尺寸效应，当岩体尺寸不小于8 m时，非均质系数的平均值和标准差分别为0.5和0.14，综合确定该岩体的REV为8 m。采用HI对三峡地下电站厂房围岩的研究表明，该岩体的REV为60 m，可作为非连续介质方法适用性的判断标准。HI是从岩体结构角度提出的新指标，适用于确定岩体的REV和统计范围，对岩体的统计分析和等效参数研究具有重要意义。
- 裂隙岩体 /
- 表征单元体 /
- 非均质系数 /
- 裂隙网络模型 /
- 尺寸效应
Abstract:
Representative elementary volume (REV) is a fundamental concept in rock mechanics and its existence is a prerequisite for estimating the equivalent parameters of rock mass and applying the continuum method to investigating the rock mass. To comprehensively consider the effects of fracture size, orientation and density on the REV of rock mass, the heterogeneity index (HI) is presented to estimate the REV. The concept and meaning of HI are elaborated and 20 random realizations of fracture network models with moderate spacing and medium persistence are implemented using the General Block software. For each realization, ten rock mass models with different sizes are selected to calculate the HI. The results show an obvious size effect of the homogeneity index. The mean value and standard deviation of the homogeneity index are 0.5 and 0.14, respectively, when the size of the rock mass is not less than 8 m, and the REV for the rock mass is determined to 8 m. The investigation of the surrounding rock mass of the underground powerhouse in the Three Gorges using the HI shows a REV size of 60 m, which can be used as a criterion for the applicability of the discontinuous method. HI is a new index proposed from the perspective of rock mass structure, which is suitable for determining the REV and statistical range of rock masses. It is of great significance for the statistical analysis and investigation of the equivalent parameters of rock masses.
- fractured rock mass /
- representative elementary volume /
- heterogeneity index /
- fracture network /
- size effect

HTML全文

图 1 中等间距-中等延展性的裂隙网络模型（模型边长20 m）

Figure 1.

下载: 全尺寸图片幻灯片

图 2 岩体非均质系数与研究区域尺寸的关系

Figure 2.

下载: 全尺寸图片幻灯片

图 3 非均质系数标准差与研究区域尺寸的关系

Figure 3.

下载: 全尺寸图片幻灯片

图 4 三峡地下电站厂房岩体非均质系数与尺寸的关系

Figure 4.

下载: 全尺寸图片幻灯片

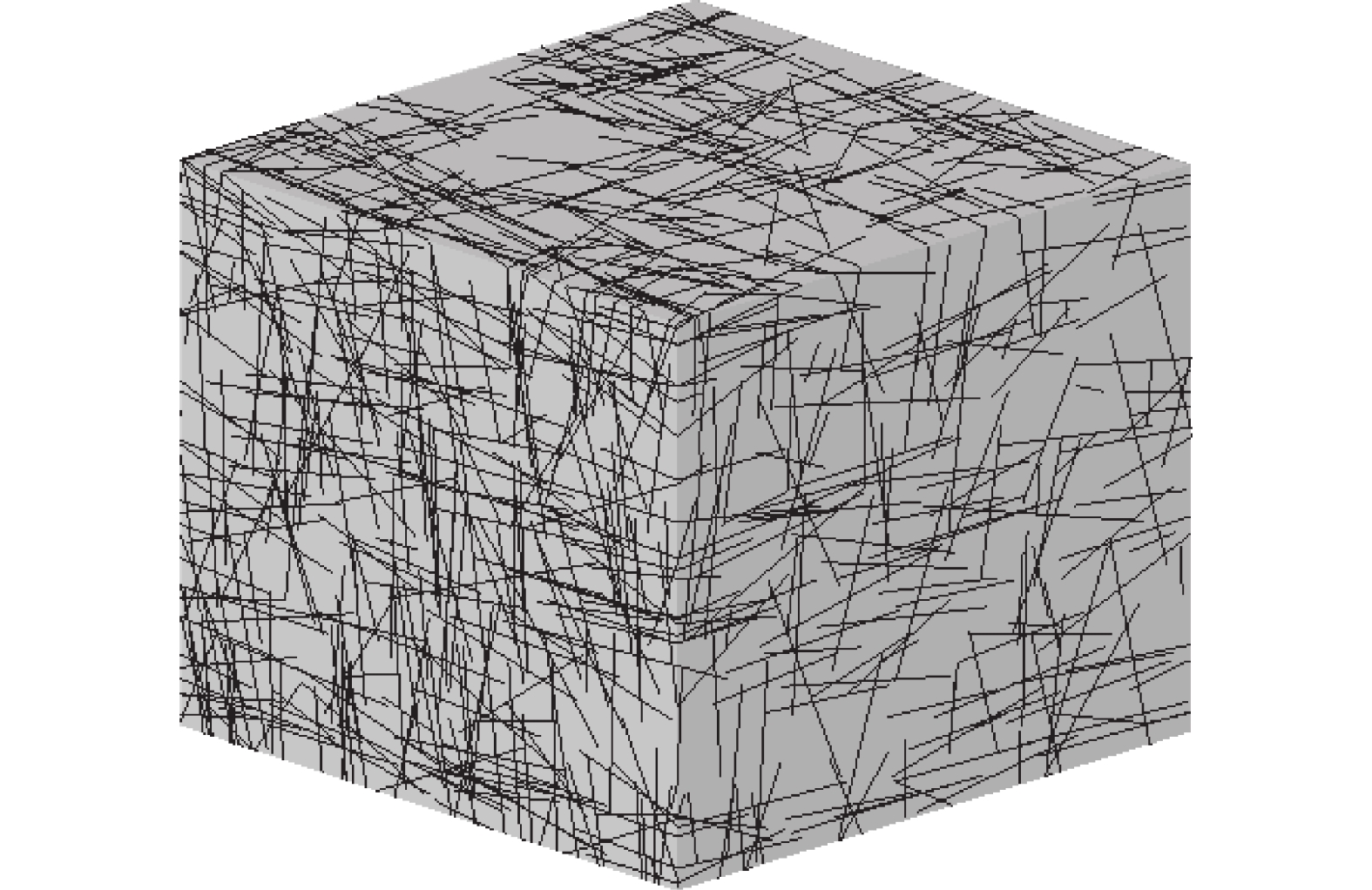
表 1 中等间距-中等延展性裂隙网络模型参数表

Table 1. Parameters for generating the discrete fracture network of the MS1-MP1 model

裂隙组号	1	2	3
半径分布形式	正态分布	正态分布	正态分布
半径均值/m	3.25	3.25	3.25
半径标准差/m	0.5	0.5	0.5
产状分布形式	Fisher分布	Fisher分布	Fisher分布
平均倾向/（°）	0	90	180
平均倾角/（°）	0	90	90
参数κ	20	20	20
三维密度/（条·m⁻³）	0.075 3	0.075 3	0.075 3

下载: 导出CSV

表 2 中等间距-中等延展性裂隙岩体模拟裂隙参数

Table 2. Parameters for the simulated fractures of the MS1-MP1 rock mass

裂隙组号	1	2	3
半径分布形式	正态分布	正态分布	正态分布
半径均值/m	3.34	3.35	3.37
半径标准差/m	0.56	0.58	0.55
产状分布形式	Fisher分布	Fisher分布	Fisher分布
平均倾向/（°）	341.7	86.7	183.7
平均倾角/（°）	2.2	89.0	87.1
参数κ	20.5	24.0	24.2
三维密度/（条·m⁻³）	0.075 3	0.075 3	0.075 3

下载: 导出CSV

表 3 三峡地下电站厂房围岩裂隙参数表^[23]

Table 3. Fracture parameters of the surrounding rock mass of the underground powerhouse in the Three Gorges

裂隙组号	1	2	3
半径分布形式	对数正态	对数正态	对数正态
半径均值/m	4.48	4.81	5.19
半径标准差/m	2.98	2.81	2.92
产状分布形式	Fisher分布	Fisher分布	Fisher分布
平均倾向/（°）	80.07	261.77	355.76
平均倾角/（°）	40.22	47.52	71.70
参数κ	9.50	7.80	10.19
三维密度/（条·m^-3）	0.002 834	0.002 626	0.002 775

下载: 导出CSV

参考文献(23)

[1]	王晓明, 郑银河. 裂隙岩体表征单元体及尺寸效应研究进展[J]. 岩土力学,2015,36(12):3456 − 3464. [WANG Xiaoming, ZHENG Yinhe. Review of advances in investigation of representative elementary volume and scale effect of fractured rock masses[J]. Rock and Soil Mechanics,2015,36(12):3456 − 3464. (in Chinese with English abstract)
[2]	XIA L, ZHENG Y H, YU Q C. Estimation of the REV size for blockiness of fractured rock masses[J]. Computers and Geotechnics,2016,76:83 − 92.
[3]	夏露, 谢娟, 于青春. 裂隙延展性统计分布离散性对岩体块体化程度REV的影响[J]. 水文地质工程地质,2019,46(4):112 − 118. [XIA Lu, XIE Juan, YU Qingchun. Influence of statistical distribution dispersion in the fracture size on blockiness REV of fractured rock masses[J]. Hydrogeology & Engineering Geology,2019,46(4):112 − 118. (in Chinese with English abstract)
[4]	ZHANG W, CHEN J P, CAO Z X, et al. Size effect of RQD and generalized representative volume elements: a case study on an underground excavation in Baihetan dam, Southwest China[J]. Tunnelling and Underground Space Technology,2013,35:89 − 98.
[5]	张文, 陈剑平, 苑晓青, 等. 基于三维裂隙网络的RQD尺寸效应与空间效应的研究[J]. 岩石力学与工程学报,2012,31(7):1437 − 1445. [ZHANG Wen, CHEN Jianping, YUAN Xaoqing, et al. Study of size effect and spatial effect of RQD for rock masses based on three-dimensional fracture network[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1437 − 1445. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-6915.2012.07.017
[6]	安玉华, 王清. 基于三维裂隙网络的裂隙岩体表征单元体研究[J]. 岩土力学,2012,33(12):3775 − 3780. [AN Yuhua, WANG Qing. Analysis of representative element volume size based on 3D fracture network[J]. Rock and Soil Mechanics,2012,33(12):3775 − 3780. (in Chinese with English abstract)
[7]	王晓明, 夏露, 郑银河, 等. 基于三维裂隙连通率的裂隙岩体表征单元体研究[J]. 岩石力学与工程学报,2013,32(增刊 2):3297 − 3302. [WANG Xaoming, XIA Lu, ZHENG Yinhe, et al. Study of representative elementary volume for fractured rock mass based on three-dimensional fracture connectivity[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(Sup 2):3297 − 3302. (in Chinese with English abstract)
[8]	SONG S Y, SUN F Y, CHEN J P, et al. Determination of RVE size based on the 3D fracture persistence[J]. Quarterly Journal of Engineering Geology and Hydrogeology,2017,50(1):60 − 68.
[9]	KHANI A, BAGHBANAN A, HASHEMOLHOSSEINI H. Numerical investigation of the effect of fracture intensity on deformability and REV of fractured rock masses[J]. International Journal of Rock Mechanics and Mining Sciences,2013,63:104 − 112.
[10]	YANG J P, CHEN W Z, DAI Y H, et al. Numerical determination of elastic compliance tensor of fractured rock masses by finite element modeling[J]. International Journal of Rock Mechanics and Mining Sciences,2014,70:474 − 482.
[11]	LAGHAEI M, BAGHBANAN A, HASHEMOLHOSSEINI H, et al. Numerical determination of deformability and strength of 3D fractured rock mass[J]. International Journal of Rock Mechanics and Mining Sciences,2018,110:246 − 256.
[12]	CUI Z, ZHANG Y H, SHENG Q, et al. Investigating the scale effect of rock mass in the Yangfanggou hydropower plant with the discrete fracture network engineering approach[J]. International Journal of Geomechanics,2020,20(4):04020033.
[13]	张莉丽, 张辛, 王云, 等. 非常低延展性裂隙岩体REV存在性研究[J]. 水文地质工程地质,2011,38(5):20 − 25. [ZHANG Lili, ZHANG Xin, WANG Yun, et al. Determining of the REV for fracture rock mass of very low ductility[J]. Hydrogeology & Engineering Geology,2011,38(5):20 − 25. (in Chinese with English abstract)
[14]	牛玉龙, 王媛, 于可, 等. 裂隙网络非达西渗流REV及非达西系数张量研究[J]. 水利学报,2020,51(4):468 − 478. [NIU Yulong, WANG Yuan, YU Ke, et al. Non-Darcy seepage REV and non-Darcy coefficient tensor in fracture network[J]. Journal of Hydraulic Engineering,2020,51(4):468 − 478. (in Chinese with English abstract)
[15]	陈庆发, 郑文师, 牛文静, 等. 裂隙岩体几何与力学尺寸效应的关联性研究[J]. 岩石力学与工程学报,2019,38(增刊 1):2857 − 2870. [CHEN Qingfa, ZHENG Wenshi, NIU Wenjing, et al. Correlation of the geometrical and mechanical size effects of fractured rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(Sup 1):2857 − 2870. (in Chinese with English abstract)
[16]	郑俊, 邓建辉, 魏进兵. 不连续面产状Fisher分布拟合度检验方法的改进[J]. 岩石力学与工程学报,2015,34(8):1561 − 1568. [ZHENG Jun, DENG Jianhui, WEI Jinbing. An improved method of goodness-of-fit test for fisher distribution to discontinuity orientations[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1561 − 1568. (in Chinese with English abstract)
[17]	于青春, 陈德基, 薛果夫, 等. 裂隙岩体一般块体理论初步[J]. 水文地质工程地质,2005,32(6):42 − 48. [YU Qingchun, CHEN Deji, XUE Guofu, et al. Preliminary study on general block method of fractured rock mass[J]. Hydrogeology & Engineering Geology,2005,32(6):42 − 48. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-3665.2005.06.011
[18]	于青春, 薛果夫, 陈德基. 裂隙岩体一般块体理论[M]. 北京: 中国水利水电出版社, 2007. YU Qingchun, XUE Guofu, CHEN Deji. General block theory of fractured rock mass [M]. Beijing: China Water Power Press, 2007.(in Chinese)
[19]	YU Q, OHNISHI Y, XUE G, et al. A generalized procedure to identify three-dimensional rock blocks around complex excavations[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2009,33(3):355 − 375.
[20]	王晓明. 乌东德坝区岩体裂隙及块体研究[D]. 北京: 中国地质大学(北京), 2013. WANG Xaoming. Study on rock fractures and rock blocks in Wudongde dam area[D]. Beijing: China University of Geosciences, 2013.(in Chinese with English abstract)
[21]	陈庆发, 牛文静, 郑文师, 等. 裂隙岩体块体化程度评价方法的若干问题修正[J]. 岩土力学,2018,39(10):3727 − 3734. [CHEN Qingfa, NIU Wenjing, ZHENG Wenshi, et al. Correction of the problems of blockiness evaluation method for fractured rock mass[J]. Rock and Soil Mechanics,2018,39(10):3727 − 3734. (in Chinese with English abstract)
[22]	ZHANG L, SHERIZADEH T, ZHANG Y W, et al. Stability analysis of three-dimensional rock blocks based on general block method[J]. Computers and Geotechnics,2020,124:103621.
[23]	夏露. 三峡工程地下电站厂房岩石块体研究[D]. 北京: 中国地质大学(北京), 2011. XIA Lu. Rock blocks in the rock around the underground powerhouse of Three Gorges project[D]. Beijing: China University of Geosciences, 2011.(in Chinese with English abstract)