An improved method for inhomogeneous space grid in the simulation of unsaturated flow
-
摘要:
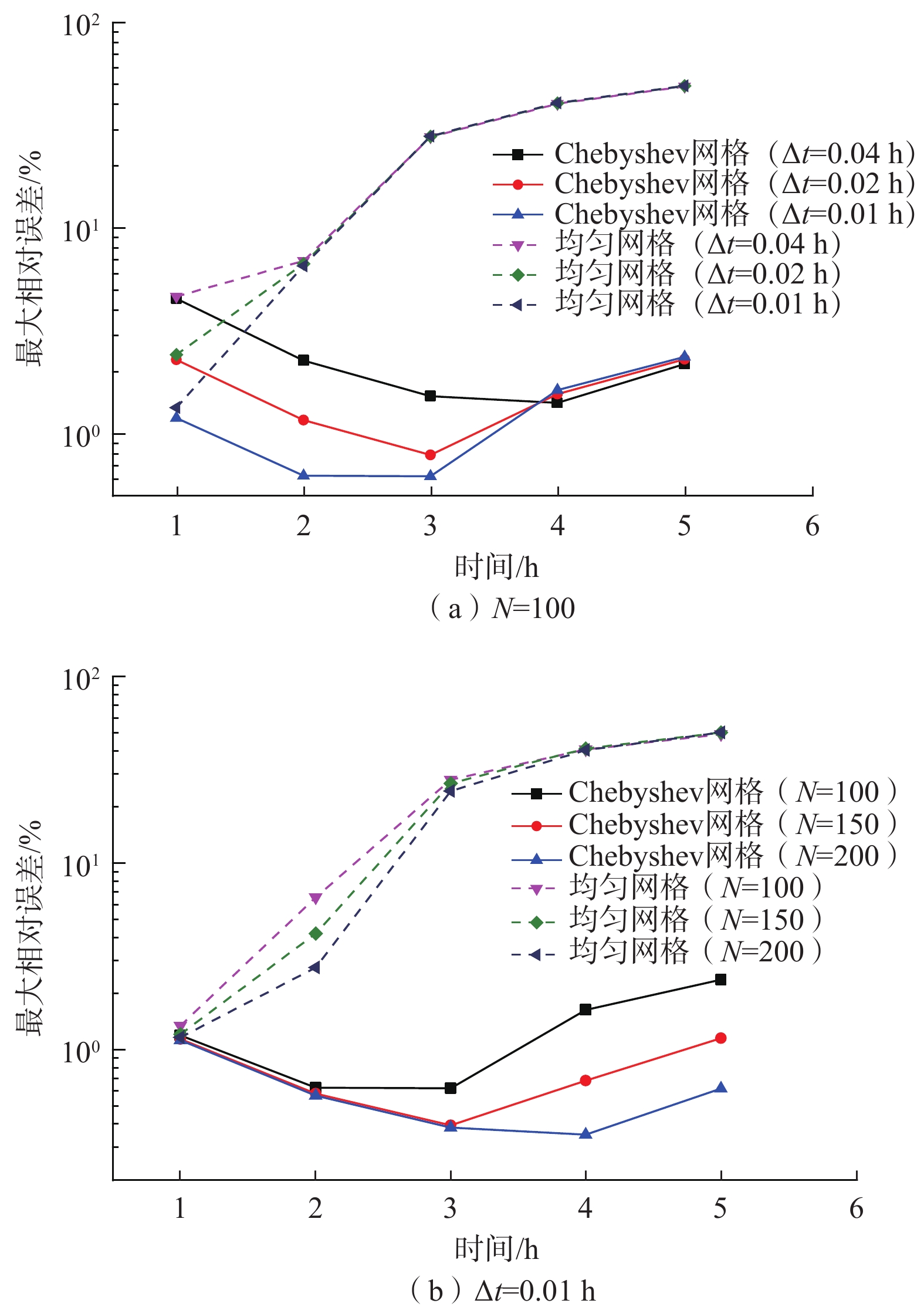
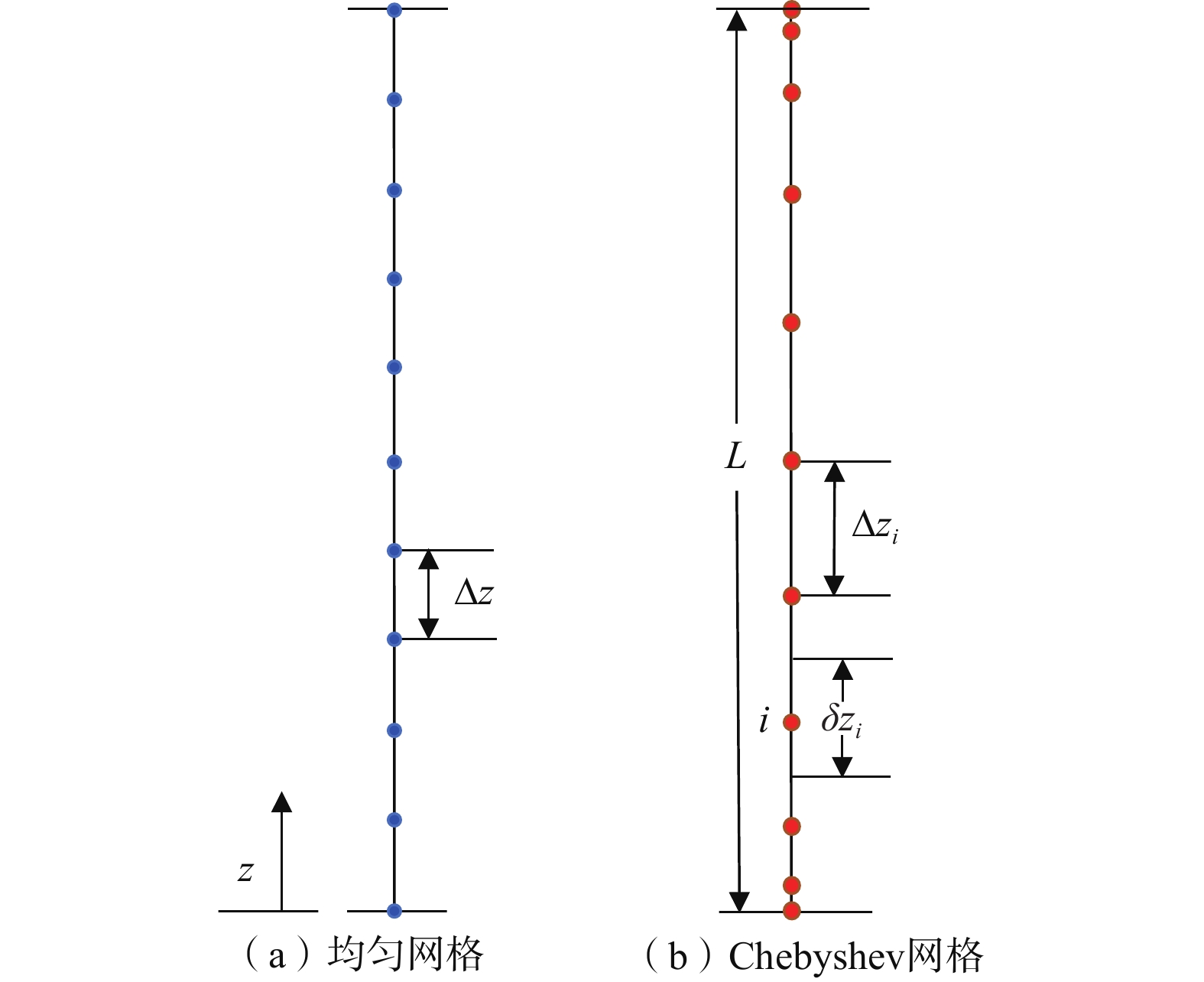
Richards方程在非饱和渗流模拟及其他相关领域应用广泛。在数值求解过程中,可以采用有限差分方法进行数值离散并迭代求解,为了获得较可靠的数值解,常规的均匀网格空间步长往往是较小的。在一些不利数值条件下,如入渗于干燥土壤,迭代计算费时甚至精度也不能得到很好改善。因此,文章提出Chebyshev空间网格改进方法,结合有限差分方法对Richards方程进行数值离散以获得线性方程组,并通过经典的Picard迭代方法进行迭代求解线性方程组以得到Richards方程的数值解。通过均质土和分层土2个不利情况下的非饱和渗流算例,又结合模型解析解和软件Hydrus-1D,对比研究了改进网格方法与均匀网格方法获得数值解的精度。结果表明,提出的Chebyshev网格方法相较于传统的均匀网格,可以在较少的节点数下获得较高的数值精度,又具有较小的计算开销,有较好的应用前景。
-
关键词:
- Richards方程 /
- 有限差分 /
- 均匀网格 /
- Chebyshev网格 /
- 数值精度
Abstract:The Richards’ equation is widely used in the simulation of unsaturated flow and related fields. In the numerical solution process, the finite difference method can be used to carry out numerical discretization and iterative calculation. However, in order to obtain a more reliable numerical solution, the space step size of a conventional uniform grid is often small. For some unfavorable numerical conditions, such as infiltration into dry soil, iterative calculation is time-consuming and even the accuracy cannot be improved very well. Therefore, an improved method is proposed by using the Chebyshev space grid, which combines the finite difference method to numerically discretize the Richards’ equation to obtain linear equations. Then the classic Picard iterative method is used to iteratively solve the linear equations to obtain the numerical solutions of the Richards’ equations. Through two examples of unsaturated flow under unfavorable conditions for homogeneous soil and layered soil, combined with the analytical solution of the model and the software Hydrus-1D, the accuracy of the numerical solution obtained by the improved grid method and the uniform grid method is compared and examined. The results show that the proposed Chebyshev grid method can obtain higher numerical accuracy with a smaller number of nodes than the traditional uniform grid, and the computational cost is smaller. This method has a good application prospect.
-
Key words:
- Richards’ equation /
- finite difference /
- uniform grid /
- Chebyshev grid /
- numerical accuracy
-

-
表 1 t=5 h时的数值精度
Table 1. Numerical accuracy at t=5 h
条件 RSE RE/% N 均匀网格法 Chebyshev网格法 均匀网格法 Chebyshev网格法 100 0.11 4.7×10−3 5.01 0.0502 150 0.10 2.6×10−3 4.53 0.1217 200 0.09 2.1×10−3 4.05 0.1476 表 2 饱和土壤的水力传导系数
Table 2. Hydraulic conductivity values for saturated soils
土壤类型 饱和水力传导系数/(m·s−1) 无杂质的砂石 10−2~1 粗砂 10−4~10−2 细砂 10−5~10−4 粉土 10−7~10−5 黏土 <10−8 表 3 工况1至8的水力传导系数
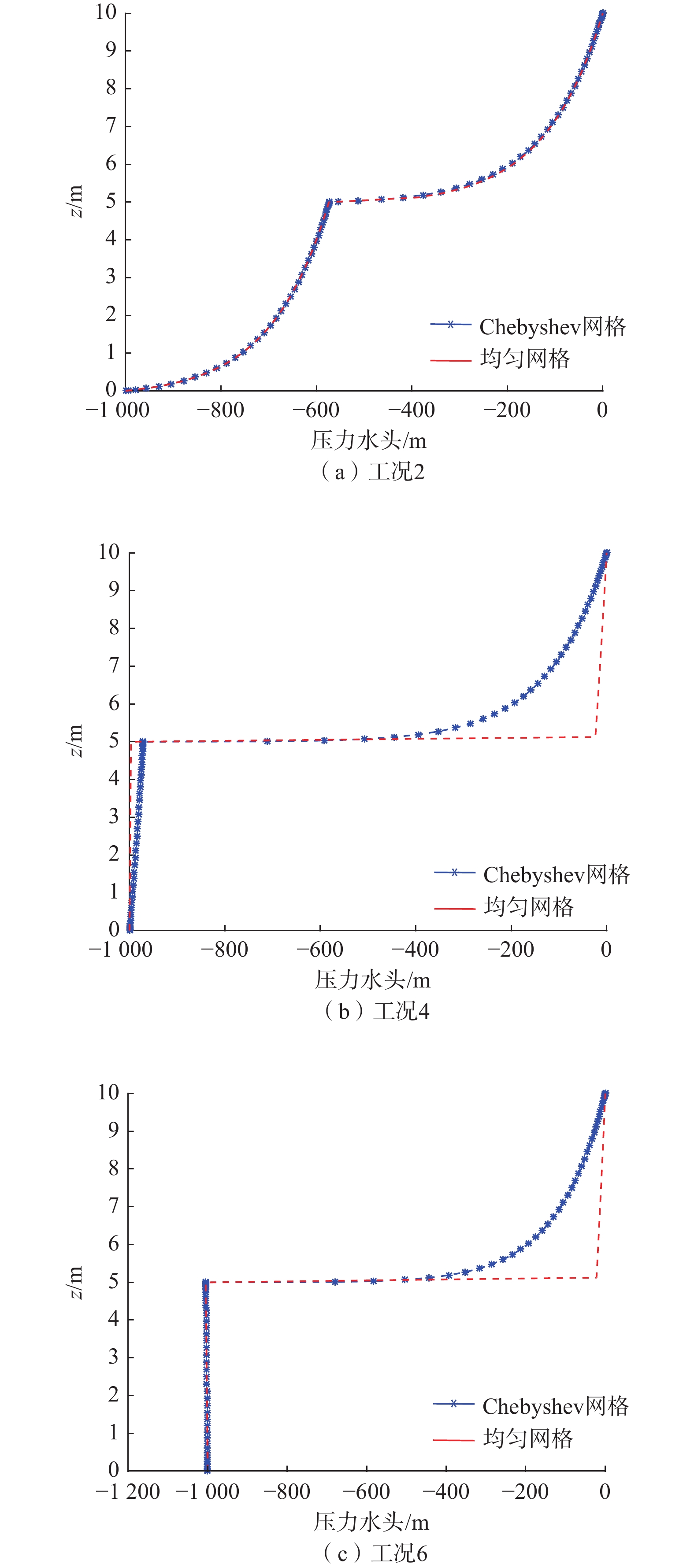
Table 3. Hydraulic conductivity for cases 1 to 8
工况数 1 2 3 4 5 6 7 8 Ks1/
(m·s−1)10−1 10−1 10−1 10−1 10−1 10−1 10−1 10−1 Ks2/
(m·s−1)10−2 10−3 10−4 10−5 10−6 10−7 10−8 10−9 表 4 数值精度比较
Table 4. Comparison of the numerical accuracy
方法 RSE RE/% MRE/% 均匀网格 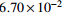
2.81 45.1 Chebyshev网格 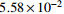
2.20 34.2 -
[1] 唐扬,殷坤龙,唐子珺. 基于HYDRUS的三舟溪滑坡降雨入渗规律研究[J]. 水文地质工程地质,2017,44(1):152 − 156. [TANG Yang,YIN Kunlong,TANG Zijun. Research on the regulation of rain infiltration in the Sanzhouxi landslide based on HYDRUS[J]. Hydrogeology & Engineering Geology,2017,44(1):152 − 156. (in Chinese with English abstract)
[2] 朱帅润,李绍红,何博,等. 改进的Picard法在非饱和土渗流中的应用研究[J]. 岩土工程学报,2022,44(4):712 − 720. [ZHU Shuairun,LI Shaohong,HE Bo,et al. Application of improved Picard method in unsaturated seepage[J]. Chinese Journal of Geotechnical Engineering,2022,44(4):712 − 720. (in Chinese with English abstract)
[3] 陈亮胜,韦秉旭,廖欢,等. 膨胀土边坡非饱和渗流及渐进性破坏耦合分析[J]. 水文地质工程地质,2020,47(4):132 − 140. [CHEN Liangsheng,WEI Bingxu,LIAO Huan,et al. A coupling analysis of unsaturated seepage and progressive failure of an expansive soil slope[J]. Hydrogeology & Engineering Geology,2020,47(4):132 − 140. (in Chinese with English abstract)
[4] 王磊,李荣建,杨正午,等. 强降雨作用下黄土陡坡开裂特性测试[J]. 吉林大学学报(地球科学版),2021,51(5):1338 − 1346. [WANG Lei,LI Rongjian,YANG Zhengwu,et al. Experimental study on cracking characteristics of loess steep slope under intensive rainfall[J]. Journal of Jilin University (Earth Science Edition),2021,51(5):1338 − 1346. (in Chinese with English abstract)
[5] 张弛,仵彦卿,覃荣高. 渗透系数升尺度对非均质含水层溶质迁移影响研究[J]. 水文地质工程地质,2014,41(5):19 − 25. [ZHANG Chi,WU Yanqing,QIN Ronggao. Research on effects of hydraulic conductivity upscaling on groundwater solute transport in heterogeneous aquifer[J]. Hydrogeology & Engineering Geology,2014,41(5):19 − 25. (in Chinese with English abstract)
[6] 刘争宏,王华山,周远强,等. 安哥拉Quelo砂场地非饱和渗流试验与计算[J]. 水文地质工程地质,2018,45(4):79 − 85. [LIU Zhenghong,WANG Huashan,ZHOU Yuanqiang,et al. Test and calculation of unsaturated seepage in the Angola Quelo sandy soil site[J]. Hydrogeology & Engineering Geology,2018,45(4):79 − 85. (in Chinese with English abstract)
[7] 周宏伟,刘泽霖,孙晓彤,等. 深部煤体注水过程中渗流通道演化特征[J]. 煤炭学报,2021,46(3):867 − 875. [ZHOU Hongwei,LIU Zelin,SUN Xiaotong,et al. Evolution characteristics of seepage channel during water infusion in deep coal samples[J]. Journal of China Coal Society,2021,46(3):867 − 875. (in Chinese with English abstract)
[8] 周淋, 杨文敬, 谢题志, 等. 苏里格气田南区莲102井区盒8段储层微观孔隙结构及气-水渗流特征[J]. 地质通报, 2022, 41(4): 682-691.
ZHOU Lin, YANG Wenjing, XIE Tizhi, et al. Reservoir micropore structure and gas-water percolation in He 8 member of well Lian 102 in south area of Sulige gas field[J]. Geological Bulletin of China, 2022, 41(4): 682-691.(in Chinese with English abstract)
[9] RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5):318–333.
[10] ZHU Shuairun,WU Lizhou,PENG Jianbing. An improved Chebyshev semi-iterative method for simulating rainfall infiltration in unsaturated soils and its application to shallow landslides[J]. Journal of Hydrology,2020,590:125157. doi: 10.1016/j.jhydrol.2020.125157
[11] 王睿,周宏伟,卓壮,等. 非饱和土空间分数阶渗流模型的有限差分方法研究[J]. 岩土工程学报,2020,42(9):1759 − 1764. [WANG Rui,ZHOU Hongwei,ZHUO Zhuang,et al. Finite difference method for space-fractional seepage process in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering,2020,42(9):1759 − 1764. (in Chinese with English abstract)
[12] LIST F,RADU F A. A study on iterative methods for solving Richards’ equation[J]. Computational Geosciences,2016,20(2):341 − 353. doi: 10.1007/s10596-016-9566-3
[13] WU Lizhou,HUANG Jinsong,FAN Wen,et al. Hydro-mechanical coupling in unsaturated soils covering a non-deformable structure[J]. Computers and Geotechnics,2020,117:103287. doi: 10.1016/j.compgeo.2019.103287
[14] 朱帅润,吴礼舟. 加速型改进迭代法在非饱和土渗流中的应用研究[J]. 岩土力学,2022,43(3):697 − 707. [ZHU Shuairun,WU Lizhou. Application research of accelerated modified iteration method in unsaturated flow[J]. Rock and Soil Mechanics,2022,43(3):697 − 707. (in Chinese with English abstract)
[15] PARLANGE J Y,HOGARTH W L,BARRY D A,et al. Analytical approximation to the solutions of Richards’ equation with applications to infiltration,ponding,and time compression approximation[J]. Advances in Water Resources,1999,23(2):189 − 194. doi: 10.1016/S0309-1708(99)00022-6
[16] WARRICK A W,ISLAS A,LOMEN D O. An analytical solution to Richards’ equation for time-varying infiltration[J]. Water Resources Research,1991,27(5):763 − 766. doi: 10.1029/91WR00310
[17] KU Chengyu,LIU C Y,SU Yan,et al. Modeling of transient flow in unsaturated geomaterials for rainfall-induced landslides using a novel spacetime collocation method[J]. Geofluids,2018:7892789.
[18] ZHA Yuanyuan,YANG Jinzhong,YIN Lihe,et al. A modified Picard iteration scheme for overcoming numerical difficulties of simulating infiltration into dry soil[J]. Journal of Hydrology,2017,551:56 − 69. doi: 10.1016/j.jhydrol.2017.05.053
[19] 朱帅润,李绍红,钟彩尹,等. 时间分数阶的非饱和渗流数值分析及其应用[J]. 应用数学和力学,2022,43(9):966 − 975. [ZHU Shuairun, LI Shaohong, ZHONG Caiyin, et al. Numerical analysis of time fractional-order unsaturated flow and its application[J]. Applied Mathematics and Mechanics,2022,43(9):966 − 975. (in Chinese with English abstract)
[20] 罗晓辉,朱帅润,陈骄锐,等. 采用改进的SOR迭代法模拟一维非饱和土渗流的研究[J]. 中南大学学报(自然科学版),2021,52(9):3331 − 3340. [LUO Xiaohui,ZHU Shuairun,CHEN Jiaorui,et al. Simulation of one-dimensional infiltration using improved SOR iterative methods in unsaturated soils[J]. Journal of Central South University(Science and Technology),2021,52(9):3331 − 3340. (in Chinese with English abstract)
[21] LIU C Y,KU Chengyu,HUANG Chichao. Numerical solutions for groundwater flow in unsaturated layered soil with extreme physical property contrasts[J]. International Journal of Nonlinear Sciences & Numerical Simulation,2015,16(7/8):325 − 335.
[22] 陈国芳,吴丹,吕俊良. 求解渗流方程的一种修正的中心型有限体积法[J]. 吉林大学学报(理学版),2020,58(5):1135 − 1141. [CHEN Guofang,WU Dan,LV Junliang. A modified cell-centered finite volume method for solving filtration equations[J]. Journal of Jilin University (Science Edition),2020,58(5):1135 − 1141. (in Chinese with English abstract)
[23] POP I S,RADU F,KNABNER P. Mixed finite elements for the Richards’ equation:Linearization procedure[J]. Journal of Computational and Applied Mathematics,2004,168(1/2):365 − 373.
[24] CHÁVEZ-NEGRETE C,DOMÍNGUEZ-MOTA F J,SANTANA-QUINTEROS D. Numerical solution of Richards’ equation of water flow by generalized finite differences[J]. Computers and Geotechnics,2018,101:168 − 175. doi: 10.1016/j.compgeo.2018.05.003
[25] 吴梦喜. 饱和-非饱和土中渗流Richards方程有限元算法[J]. 水利学报,2009,40(10):1274 − 1279. [WU Mengxi. Finite-element algorithm for Richards’ equation for saturated-unsaturated seepage flow[J]. Journal of Hydraulic Engineering,2009,40(10):1274 − 1279. (in Chinese with English abstract) doi: 10.3321/j.issn:0559-9350.2009.10.018
[26] ZAMBRA C E,DUMBSER M,TORO E F,et al. A novel numerical method of high-order accuracy for flow in unsaturated porous media[J]. International Journal for Numerical Methods in Engineering,2012,89(2):227 − 240.
[27] DENG Baoqing,WANG Junye. Saturated-unsaturated groundwater modeling using 3D Richards equation with a coordinate transform of nonorthogonal grids[J]. Applied Mathematical Modelling,2017,50(10):39 − 52. doi: 10.1016/j.apm.2017.05.021
[28] DOLEJŠÍ V,KURAZ M,SOLIN P. Adaptive higher-order space-time discontinuous Galerkin method for the computer simulation of variably-saturated porous media flows[J]. Applied Mathematical Modelling,2019,72:276 − 305.
[29] 郑川东,刘广宁,杨中华,等. 基于梯度准则的动态局部自适应网格在浅水水流水质耦合模型求解中的应用[J]. 武汉大学学报(工学版),2021,54(9):784 − 794. [ZHENG Chuandong,LIU Guangning,YANG Zhonghua,et al. Application of dynamic local adaptive grid based on gradient criterion in solving shallow water hydrodynamics-water quality coupling model[J]. Engineering Journal of Wuhan University,2021,54(9):784 − 794. (in Chinese with English abstract)
[30] 何金辉,李明广,陈锦剑,等. 考虑动态流体网格的颗粒-流体耦合算法[J]. 上海交通大学学报,2021,55(6):645 − 651. [HE Jinhui,LI Mingguang,CHEN Jinjian,et al. Particle-fluid coupling algorithm considering dynamic fluid mesh[J]. Journal of Shanghai Jiao Tong University,2021,55(6):645 − 651. (in Chinese with English abstract)
[31] BIANCHI G,RANE S,KOVACEVIC A,et al. Deforming grid generation for numerical simulations of fluid dynamics in sliding vane rotary machines[J]. Advances in Engineering Software,2017,112:180 − 191. doi: 10.1016/j.advengsoft.2017.05.010
[32] LEHMANN F,ACKERER P. Comparison of iterative methods for improved solutions of the fluid flow equation in partially saturated porous media[J]. Transport in Porous Media,1998,31:275 − 292. doi: 10.1023/A:1006555107450
[33] GARDNER W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science,1958,85(4):228 − 232. doi: 10.1097/00010694-195804000-00006
[34] WU Lizhou,ZHU Shuairun,PENG Jianbing. Application of the Chebyshev spectral method to the simulation of groundwater flow and rainfall-induced landslides[J]. Applied Mathematical Modelling,2020,80:408 − 425. doi: 10.1016/j.apm.2019.11.043
[35] LIU C S. A two-side equilibration method to reduce the condition number of an ill-posed linear system[J]. Computer Modeling in Engineering & Sciences,2013,91(1):17 − 42.
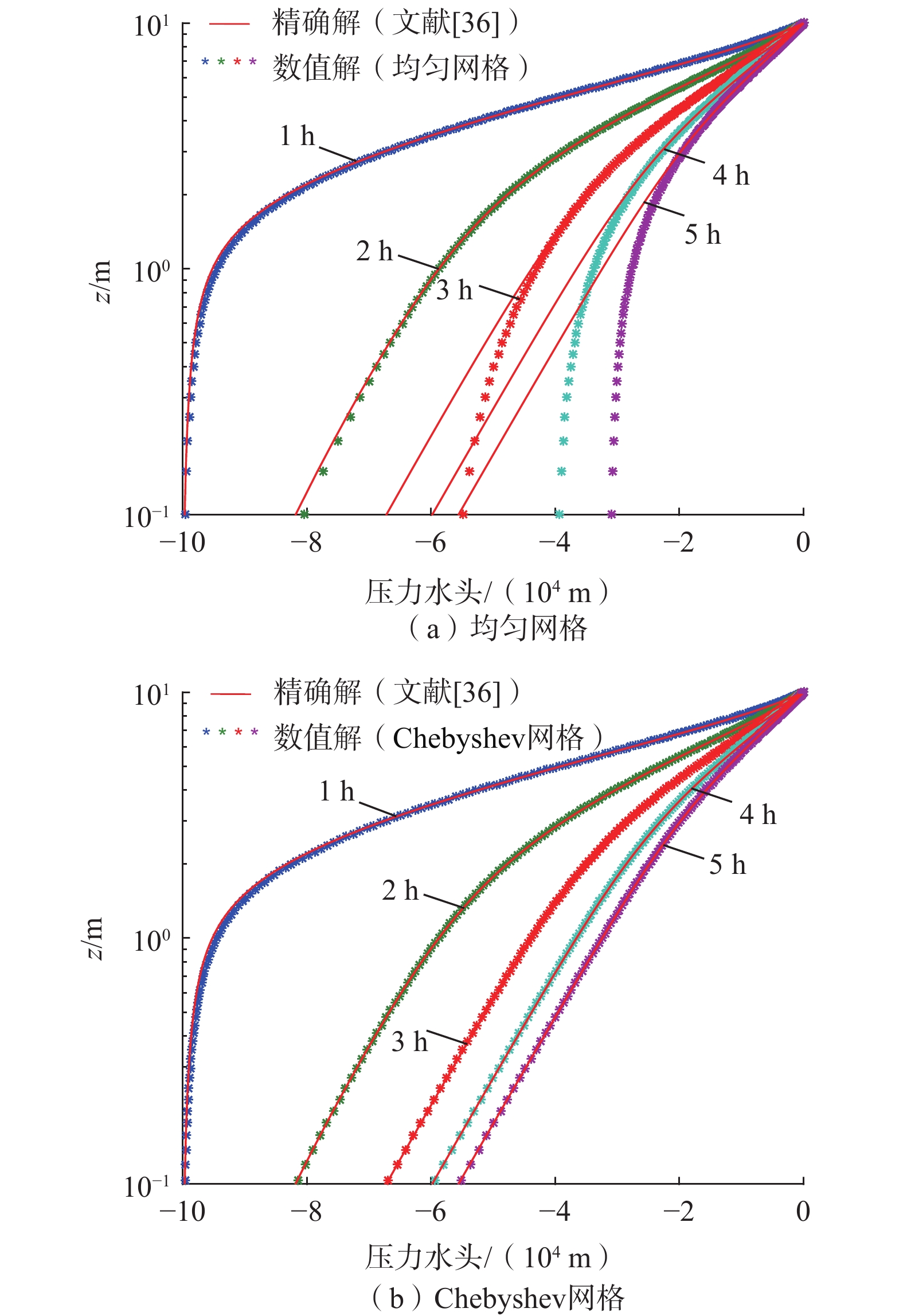
[36] TRACY F T. Clean two- and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers[J]. Water Resources Research,2006,42(8):1 − 11.
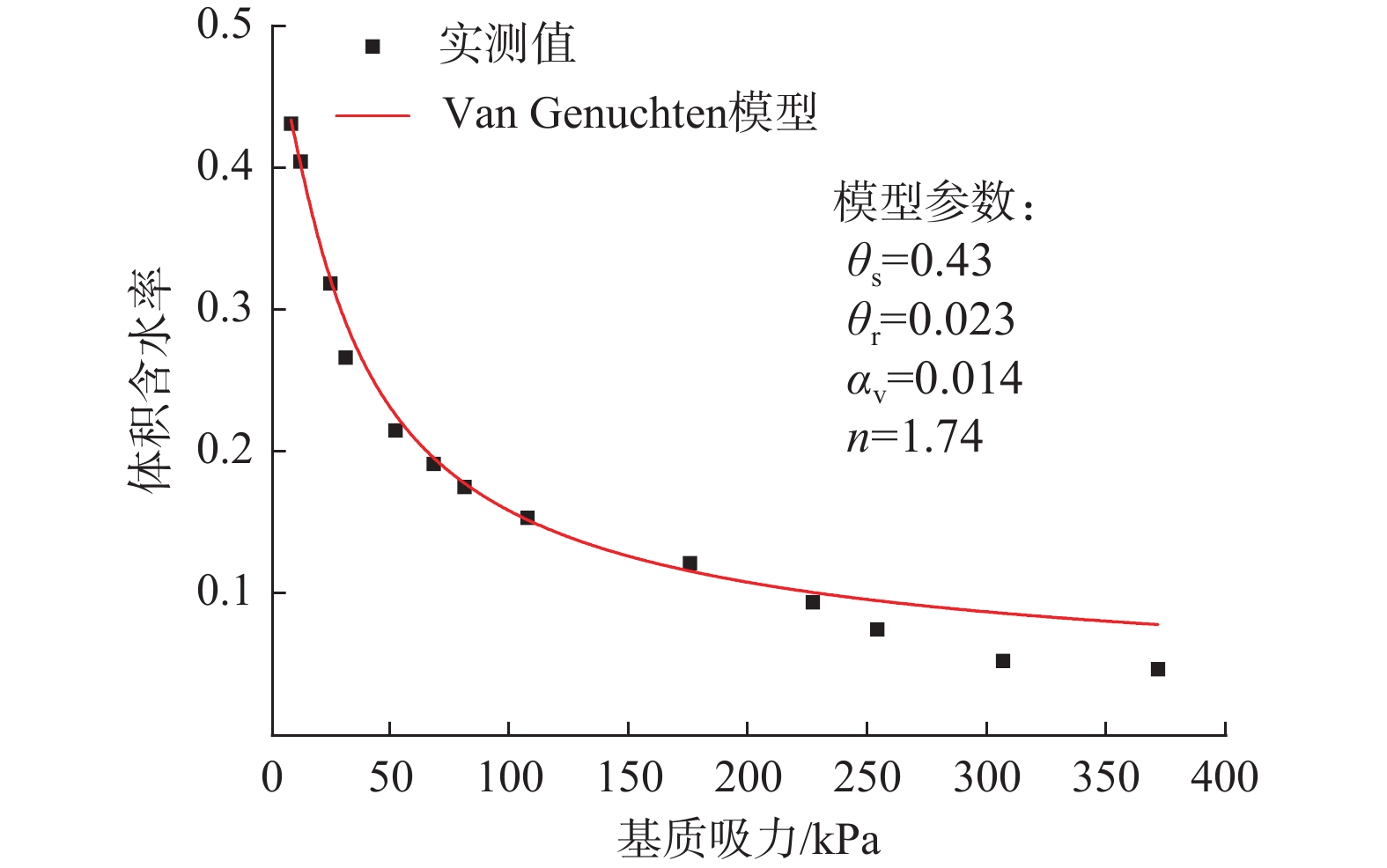
[37] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal,1980,44(5):892 − 898. doi: 10.2136/sssaj1980.03615995004400050002x
-



 下载:
下载: