Application of the bias aware Ensemble Kalman Filter with Confirming Option (Bias-CEnKF) in groundwater flow data assimilation
-
摘要:
集合卡尔曼滤波(Ensemble Kalman Filter,EnKF)方法已广泛应用于地下水水流和污染物运移模拟相关问题的求解。但前人研究多建立在同化系统预报模型是准确的基础上,忽视了模型概化的不确定性。当模型概化不准确时,将导致预报偏差,可能带来错误的系统估计。因此,文章提出考虑模型预报偏差的迭代式集合卡尔曼滤波(Bias aware Ensemble Kalman Filter with Confirming Option,Bias-CEnKF)方法。以地下水水流数据同化为例,研究模型概化存在不确定条件下,边界条件、初始条件、源汇项概化不准确时新方法的有效性。结果表明,当预报模型概化不准确时,使用标准EnKF方法进行数据同化,可能会导致滤波发散,造成同化失败。Bias-CEnKF方法不仅保留了较好的同化性能,同时减小了参数、变量、偏差项非线性关系带来的不一致性。针对文章中4种情景,Bias-CEnKF同化获得的含水层渗透系数场以及水头场均接近真实场,且预报结果可靠。本研究进一步提升了模型概化不确定时EnKF方法的适用性,为实际野外复杂条件下地下水水流数据同化问题提供了可靠的方法。
Abstract:The Ensemble Kalman Filter (EnKF) has been widely applied for real-time simulation of groundwater flow and solute transport. The majority of previous studies tend to assume no bias in forecast models, therefore ignoring the model uncertainties. This assumption, however, may be invalid when a conceptual model is not accurately generalized. As a result, forecast bias will lead to incorrect estimation of the system parameters or states. In this work, a bias aware Ensemble Kalman Filter with Confirming Option (Bias-CEnKF) is proposed to take into account the forecast bias by the model during the filtering process. The proposed method is tested in a real-time groundwater simulation considering model uncertainties, by setting inaccurate boundary conditions, initial conditions and recharge items. The results show that the standard EnKF may lead to filter divergence and assimilation failure, if the forecast model is not accurately generalized. Instead, Bias-CEnKF not only achieves better performances, but also reduces the inconsistency caused by the nonlinear relationship among the parameters, variables and bias corrections. Four scenarios are investigated, with the results showing the aquifer hydraulic conductivities and heads obtained by Bias-CEnKF are close to the real values, and the prediction results are also more reliable. This study further improves the applicability of the EnKF under the uncertain condition of model generalization, and provides a reliable method for groundwater data assimilation under complex field conditions.
-

-
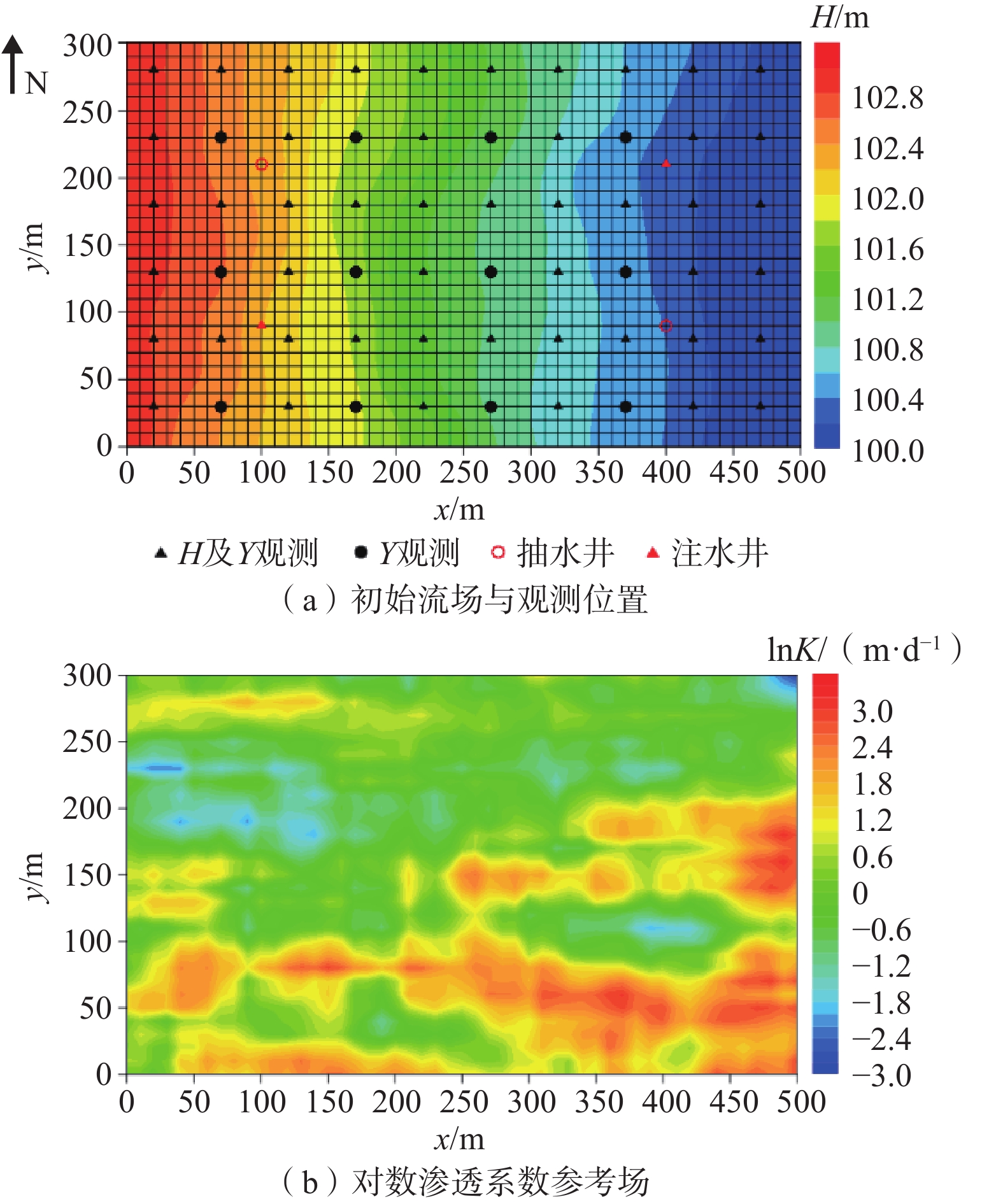
图 1 研究区初始流场与观测位置和对数渗透系数Y参考场(文献[26]有修改)
Figure 1.
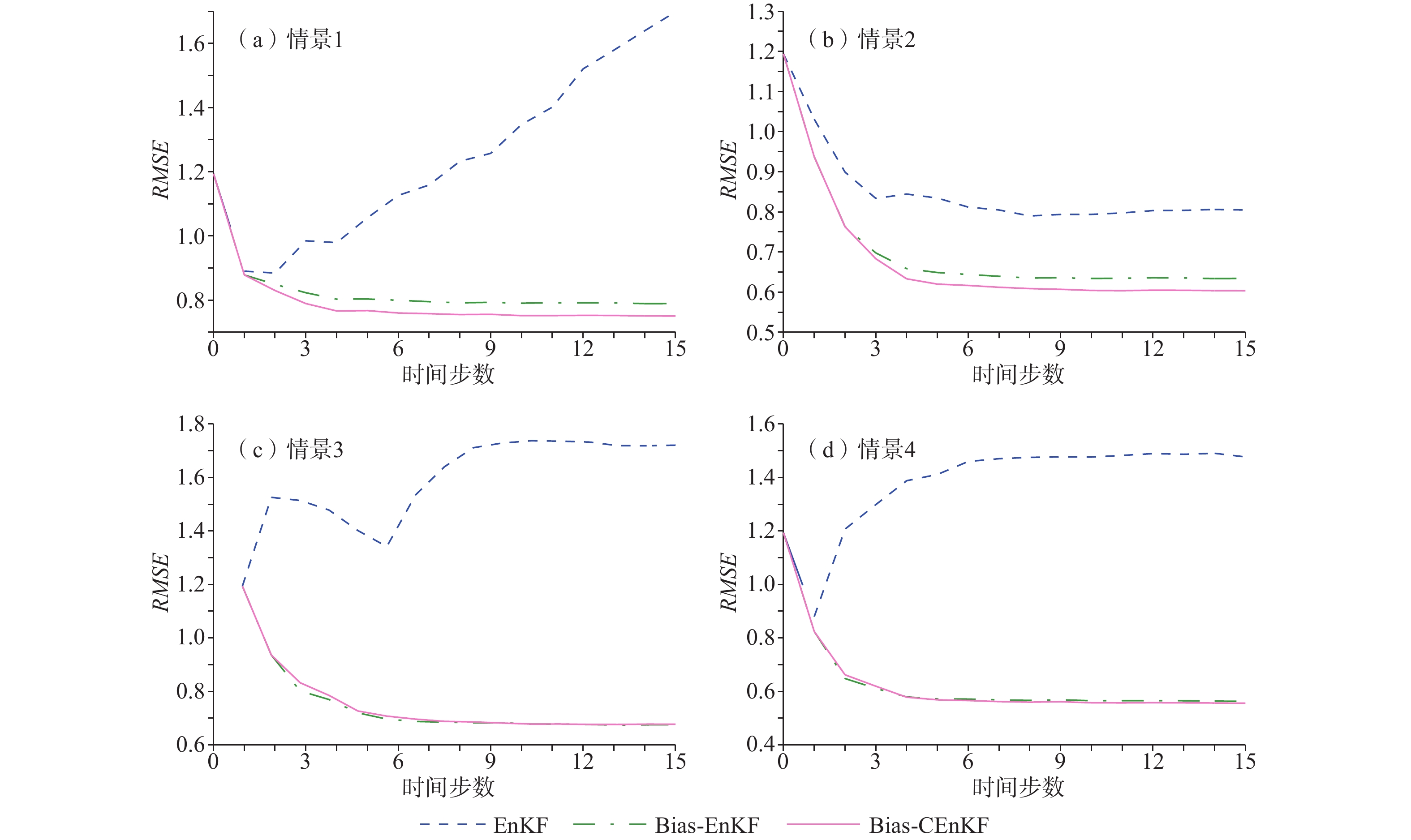
表 1 EnKF、Bias-EnKF和Bias-CEnKF同化结果对比
Table 1. Assimilation results of EnKF, Bias-EnKF and Bias-CEnKF
情景 Y场RMSE H场RMSE EnKF Bias-EnKF Bias-CEnKF EnKF Bias-EnKF Bias-CEnKF 情景1 1.70 0.79 0.75 1.52 0.63 0.56 情景2 0.80 0.63 0.60 0.75 0.46 0.36 情景3 1.72 0.68 0.68 1.10 0.54 0.48 情景4 1.48 0.56 0.56 2.25 0.39 0.34 -
[1] EVENSEN G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research:Oceans,1994,99(5):10143 − 10162. doi: 10.1029/94JC00572
[2] EVENSEN G. The Ensemble Kalman Filter:Theoretical formulation and practical implementation[J]. Ocean Dynamics,2003,53(4):343 − 367. doi: 10.1007/s10236-003-0036-9
[3] 沈晔,李海涛,黎涛,等. 地下水位预测: 集合卡尔曼滤波(EnKF)应用概述[J]. 水文地质工程地质,2014,41(1):21 − 24. [SHEN Ye, LI Haitao, LI Tao, et al. Groundwater level forecast: Overview of application of the Ensemble Kalman filter (EnKF)[J]. Hydrogeology & Engineering Geology,2014,41(1):21 − 24. (in Chinese with English abstract)
[4] 兰天, 康学远, 施小清, 等. 基于EnKF综合水头和浓度观测数据推估地下水流模型参数[J]. 水文地质工程地质,2017,44(5):6 − 13. [LAN Tian, KANG Xueyuan, SHI Xiaoqing, et al. Joint assimilation of heads and concentrations for estimating parameters of groundwater flow models using the Ensemble Kalman Filter[J]. Hydrogeology & Engineering Geology,2017,44(5):6 − 13. (in Chinese with English abstract)
[5] 刘琨, 黄冠华. 基于集合卡尔曼滤波法的二维土壤水流状态变量和参数联合估计[J]. 水利学报,2019,50(3):399 − 408. [LIU Kun, HUANG Guanhua. Joint state and parameter estimation of two-dimensional soil water flow model based on Ensemble Kalman Filter method[J]. Journal of Hydraulic Engineering,2019,50(3):399 − 408. (in Chinese with English abstract)
[6] XU T, GÓMEZ-HERNÁNDEZ J J, CHEN Z, et al. A comparison between ES-MDA and restart EnKF for the purpose of the simultaneous identification of a contaminant source and hydraulic conductivity[J]. Journal of Hydrology,2021,595:125681. doi: 10.1016/j.jhydrol.2020.125681
[7] HOUTEKAMER P L, ZHANG F Q. Review of the ensemble Kalman filter for atmospheric data assimilation[J]. Monthly Weather Review,2016,144(12):4489 − 4532. doi: 10.1175/MWR-D-15-0440.1
[8] JORDI A, WANG D P. Estimation of transport at open boundaries with an ensemble Kalman filter in a coastal ocean model[J]. Ocean Modelling,2013,64:56 − 66. doi: 10.1016/j.ocemod.2013.01.002
[9] EMERICK A, REYNOLDS A. Combining sensitivities and prior information for covariance localization in the ensemble Kalman filter for petroleum reservoir applications[J]. Computational Geosciences,2011,15(2):251 − 269. doi: 10.1007/s10596-010-9198-y
[10] 崔凯鹏, 吴吉春. 观测数据时空密度对集合卡尔曼滤波计算精度的影响[J]. 水利学报,2013,44(8):915 − 923. [CUI Kaipeng, WU Jichun. Effect of observation data time/spatial density on Ensemble Kalman Filter[J]. Journal of Hydraulic Engineering,2013,44(8):915 − 923. (in Chinese with English abstract)
[11] 曹少华, 曾献奎, 蒋建国, 等. 基于局域化集合卡尔曼滤波的含水层弥散度场识别研究[J]. 南京大学学报(自然科学版),2016,52(3):429 − 437. [CAO Shaohua, ZENG Xiankui, JIANG Jianguo, et al. An approach based on localizaed ensemble Kalman filter to identify groundwater dispersivity field[J]. Journal of Nanjing University (Natural Sciences),2016,52(3):429 − 437. (in Chinese with English abstract)
[12] 康学远, 施小清, 邓亚平, 等. 基于EnKF融合地球物理数据刻画含水层非均质性[J]. 水科学进展,2018,29(1):40 − 49. [KANG Xueyuan, SHI Xiaoqing, DENG Yaping, et al. Assimilation of hydrogeophysical data for the characterization of subsurface heterogeneity using Ensemble Kalman Filter (EnKF)[J]. Advances in Water Science,2018,29(1):40 − 49. (in Chinese with English abstract)
[13] 南统超, 吴吉春. 集合卡尔曼滤波估计水文地质参数的局域化修正[J]. 水科学进展,2010,21(5):613 − 621. [NAN Tongchao, WU Jichun. Localization corrections for the estimation of hydrogeological parameters using ensemble Kalman filter[J]. Advances in Water Science,2010,21(5):613 − 621. (in Chinese with English abstract)
[14] 张秋汝, 史良胜, 林琳, 等. 非饱和土壤水的集合卡尔曼滤波Ⅱ:不一致性问题解决方法比较[J]. 水利学报,2015,46(12):1470 − 1478. [ZHANG Qiuru, SHI Liangsheng, LIN Lin, et al. Ensemble Kalman filter for unsaturated soil water flowⅡ:Comparison of methods to deal with inconsistency[J]. Journal of Hydraulic Engineering,2015,46(12):1470 − 1478. (in Chinese with English abstract)
[15] 周海燕. 基于集合卡尔曼滤波法的非高斯含水层参数识别[D]. 北京: 中国地质大学(北京), 2012
ZHOU Haiyan. Characterizing non-Gaussian aquifer model parameters based on the ensemble Kalman filter[D]. Beijing: China University of Geosciences, 2012. (in Chinese with English abstract)
[16] XU T, GÓMEZ-HERNÁNDEZ J J. Simultaneous identification of a contaminant source and hydraulic conductivity via the restart normal-score ensemble Kalman filter[J]. Advances in Water Resources,2018,112:106 − 123. doi: 10.1016/j.advwatres.2017.12.011
[17] 钟乐乐, 曾献奎, 吴吉春. 基于高斯过程回归的地下水模型结构不确定性分析与控制[J]. 水文地质工程地质,2019,46(1):1 − 10. [ZHONG Lele, ZENG Xiankui, WU Jichun. Quantification and reduction of groundwater model structural uncertainty based on Gaussian process regression[J]. Hydrogeology & Engineering Geology,2019,46(1):1 − 10. (in Chinese with English abstract)
[18] ROJASR, FEYENL, DASSARGUES A. Conceptual model uncertainty in groundwater modeling: combining generalized likelihood uncertainty estimation and Bayesian model averaging[J]. Water Resources Research,2008,44(12):W12418.
[19] ELSHALLAS, YE M, FINKEL M. Evaluating two multi-model simulation-optimization approaches for managing groundwater contaminant plumes[J]. Journal of Hydrology,2020,590:125427. doi: 10.1016/j.jhydrol.2020.125427
[20] 孙晓卓, 曾献奎, 吴吉春, 等. 一种改进的地下水模型结构不确定性分析方法[J]. 水文地质工程地质,2021,48(6):24 − 33. [SUN Xiaozhuo, ZENG Xiankui, WU Jichun, et al. An improved method of groundwater model structural uncertainty analysis[J]. Hydrogeology & Engineering Geology,2021,48(6):24 − 33. (in Chinese with English abstract)
[21] ERDAL D, NEUWEILER I, WOLLSCHLÄGER U. Using a bias aware EnKF to account for unresolved structure in an unsaturated zone model[J]. Water Resources Research,2014,50(1):132 − 147. doi: 10.1002/2012WR013443
[22] XUE L, ZHANG D X. A multimodeldata assimilation framework via the ensemble Kalman filter[J]. Water Resources Research,2014,50(5):4197 − 4219. doi: 10.1002/2013WR014525
[23] REFSGAARD J C, VAN DER SLUIJS J P, BROWN J, et al. A framework for dealing with uncertainty due to model structure error[J]. Advances in Water Resources,2006,29(11):1586 − 1597. doi: 10.1016/j.advwatres.2005.11.013
[24] KOLLAT J B, REED P M, RIZZO D M. Addressing model bias and uncertainty in three dimensional ground water transport forecasts for a physical aquifer experiment[J]. Geophysical Research Letters,2008,35(17):L17402. doi: 10.1029/2008GL035021
[25] WEN X H, CHEN W H. Real-time reservoir model updating using ensemble Kalman filter with confirming option[J]. SPE Journal,2006,11(4):431 − 442. doi: 10.2118/92991-PA
[26] 崔凯鹏. 集合卡尔曼滤波在地下水流及溶质运移数据同化中的应用探讨[D]. 南京: 南京大学, 2013
CUI Kaipeng. The application and discussion of ensemble Kalman filter method in groundwater flow and solute transport data assimilation[D]. Nanjing: Nanjing University, 2013. (in Chinese with English abstract)
[27] 康学远, 施小清, 史良胜, 等. 基于集合卡尔曼滤波的多相流模型参数估计—以室内二维砂箱中重质非水相污染物入渗为例[J]. 吉林大学学报(地球科学版),2017,47(3):848 − 859. [KANG Xueyuan, SHI Xiaoqing, SHI Liangsheng, et al. Inverse multiphase flow simulation using ensemble Kalman filter:Application to a 2D sandbox experiment of DNAPL migration[J]. Journal of Jilin University (Earth Science Edition),2017,47(3):848 − 859. (in Chinese with English abstract)
[28] ZHANG D X, LU Z M. An efficient, high-order perturbation approach for flow in random porous media via Karhunen-Loève and polynomial expansions[J]. Journal of Computational Physics,2004,194(2):773 − 794. doi: 10.1016/j.jcp.2003.09.015
[29] HARBAUGH A W, BANTA E R, HILL M C, et al. MODFLOW-2000, the U. S. Geological survey modular ground-water model-user guide to modularization concepts and the ground-water flow process[R]. Reston: USGS, 2000.
-



 下载:
下载: