Calculation method of thrust force of the embedded stabilizing piles under the overtop-sliding failure mode
-
摘要:
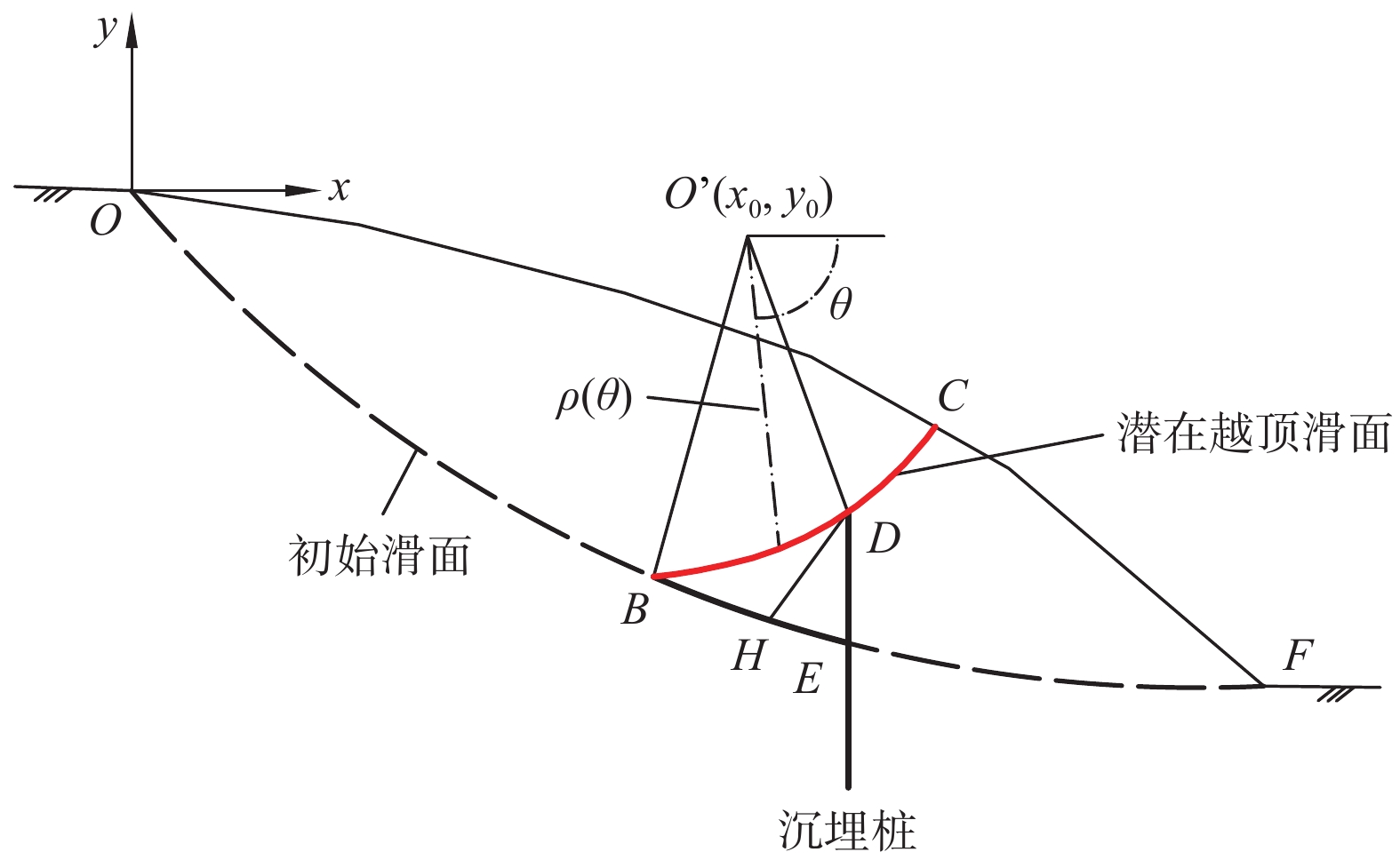
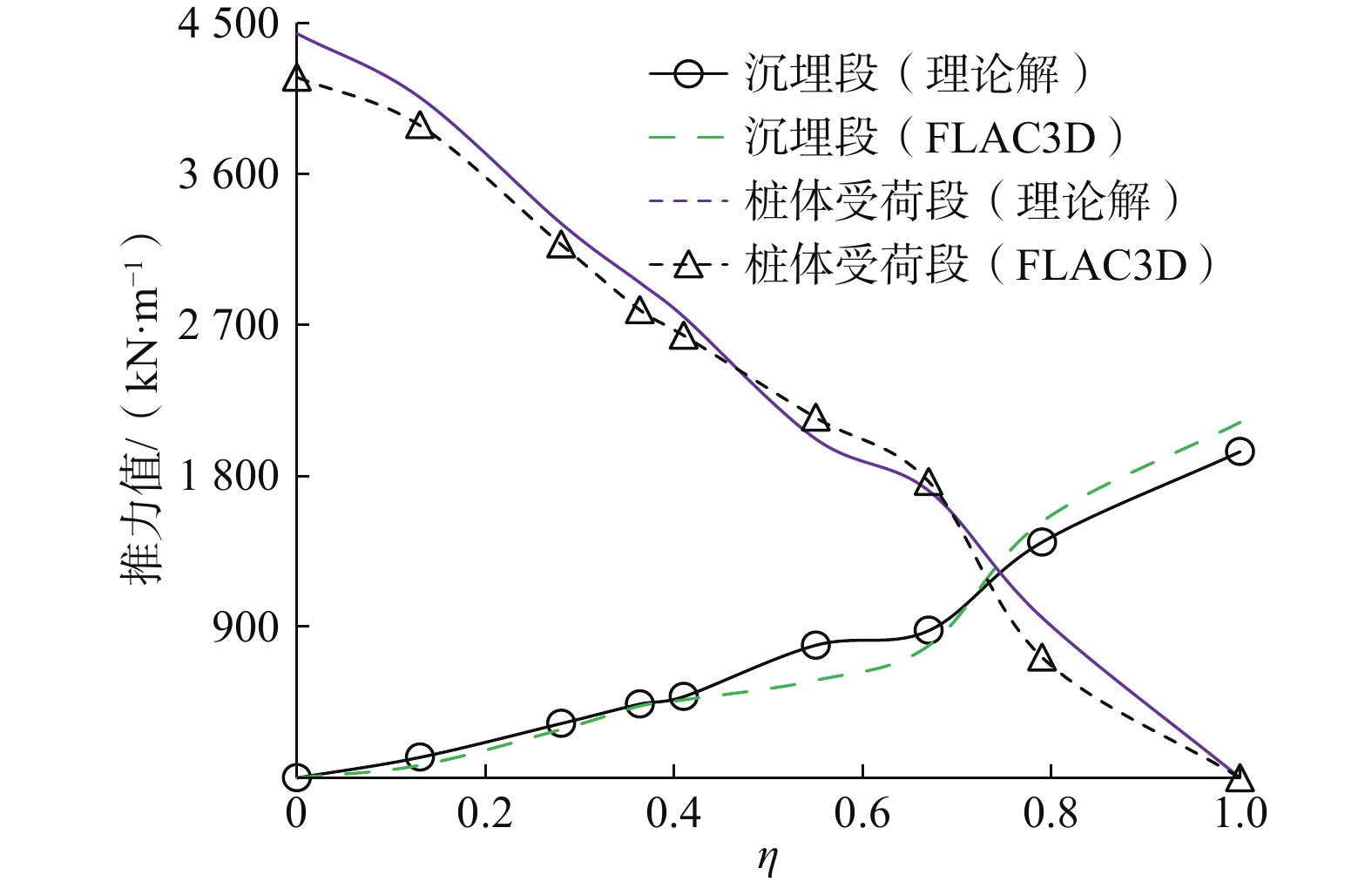
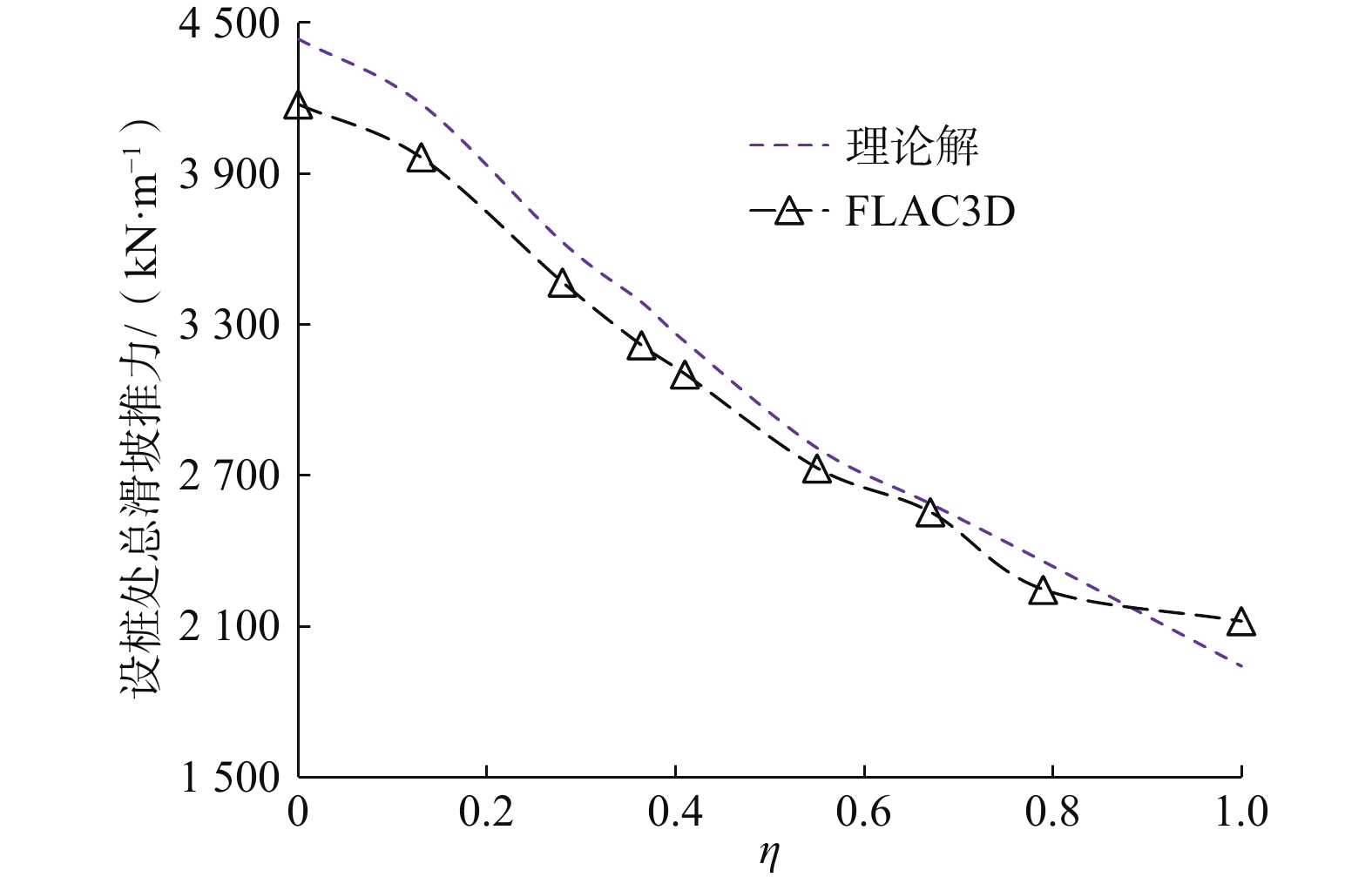
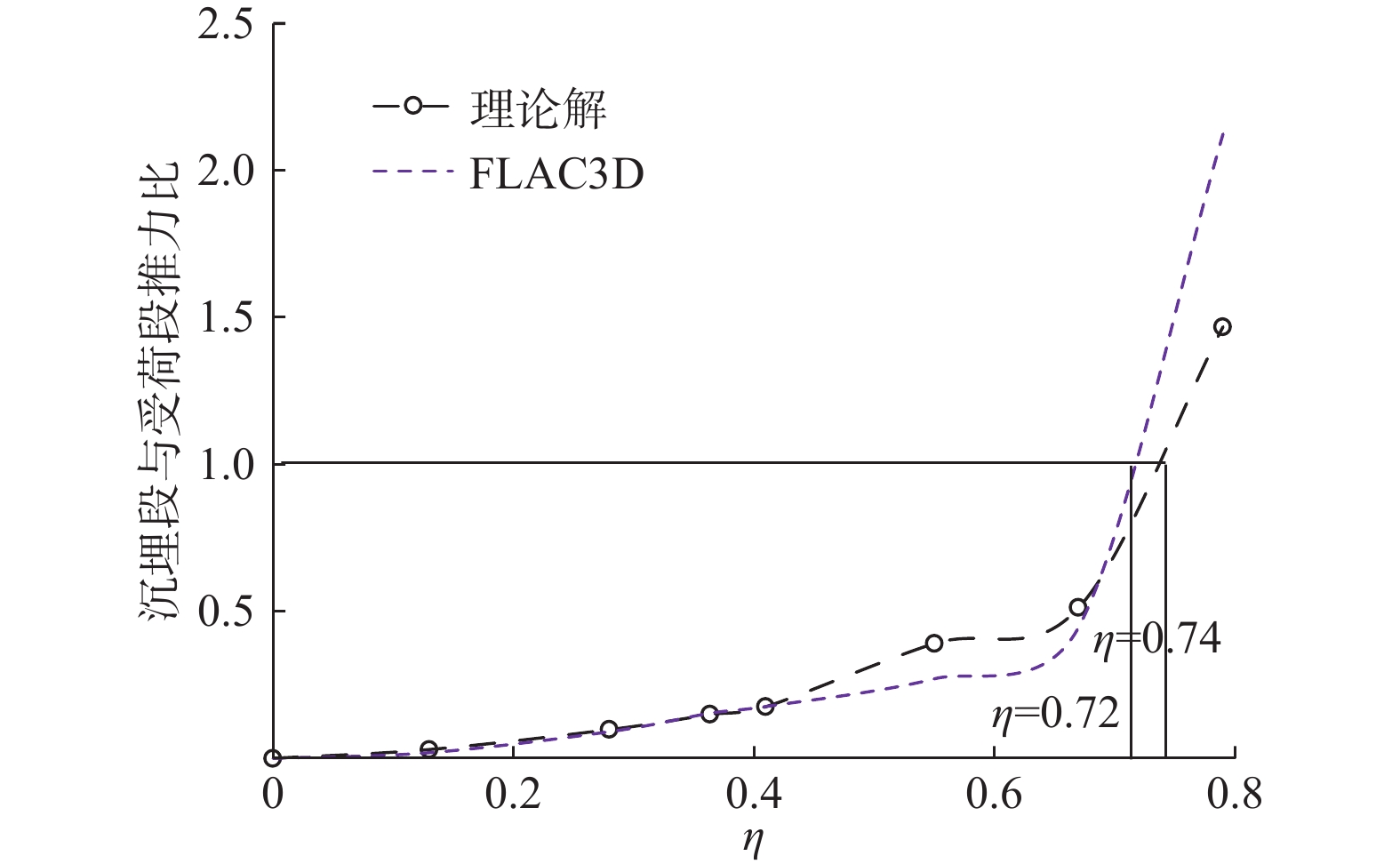
滑坡推力的确定对于抗滑桩设计极其重要,沉埋桩作为对传统抗滑桩的优化,其受荷段推力的研究目前主要借助于模型试验和数值模拟,缺乏深入的理论分析。为了建立沉埋桩后侧受荷段及桩顶沉埋段滑坡推力计算方法,针对沉埋桩加固的基岩-覆盖层式滑坡,基于潜在越顶破坏模式,由桩顶位置将越顶滑面分为顶部、底部两段,其中,顶部滑面上水平方向合力即为沉埋段推力,可由积分求得,底部滑面上各个方向的力求解方法与此类似;在此基础上,利用刚体极限平衡理论对底部滑面与桩受荷段所围滑体进行受力分析,进而可得受荷段推力计算公式。实例分析表明:理论算法所得沉埋段与受荷段推力值与FLAC3D结果非常接近,其中,受荷段推力、沉埋段推力、设桩位置处总推力随沉埋比的增大而分别非线性减小、增大、减小;沉埋比位于0~0.67范围内时,沉埋段与受荷段推力之比由0缓慢增大到0.30~0.50,随着沉埋比增大到0.8,该比值急剧增大到1.47~2.12;一般沉埋深度下,沉埋段推力小于受荷段推力。沉埋桩推力的理论研究对于桩体内力优化、沉埋深度确定具有重要的现实意义,将有助于该桩型的进一步推广应用。
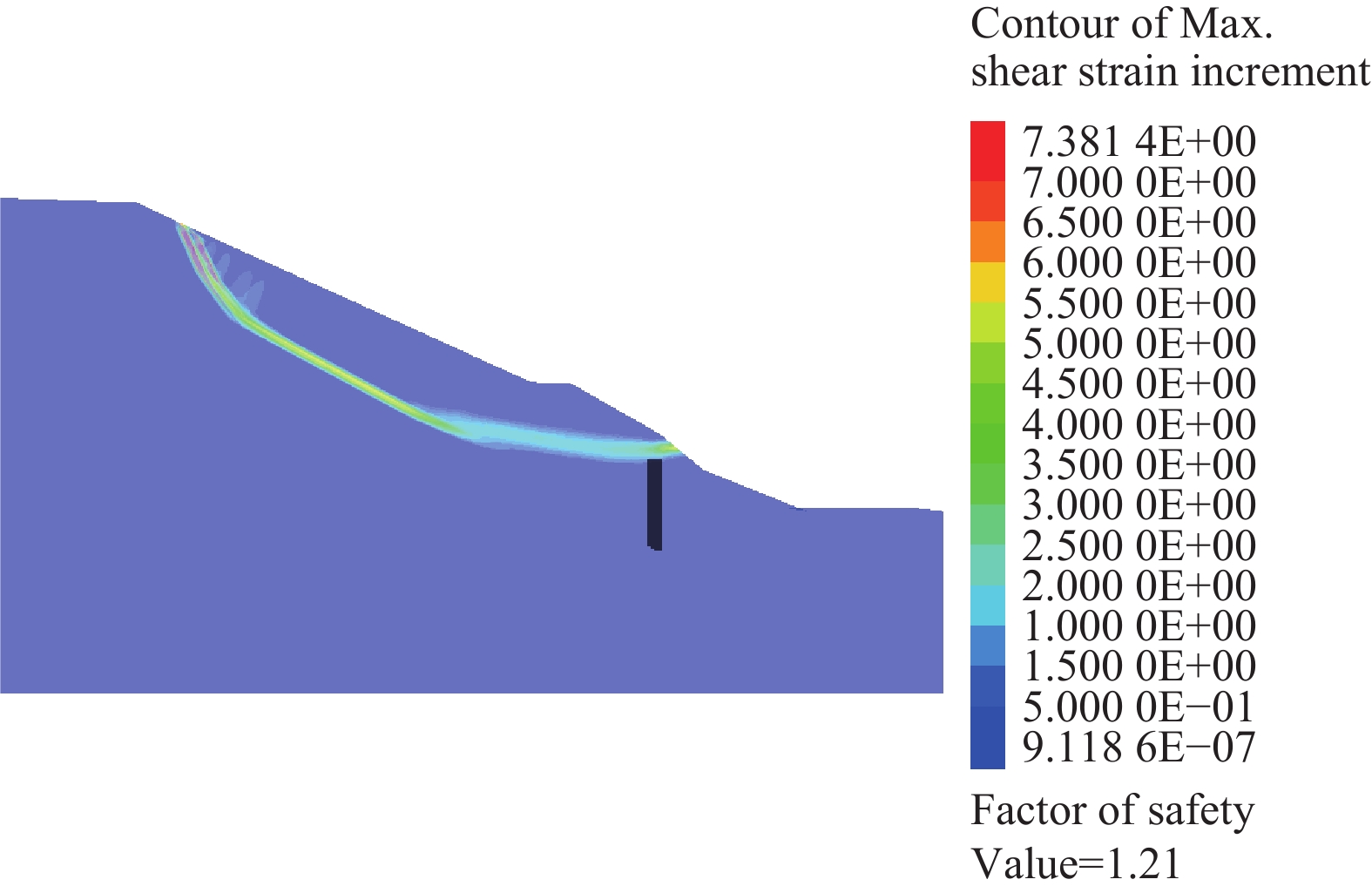
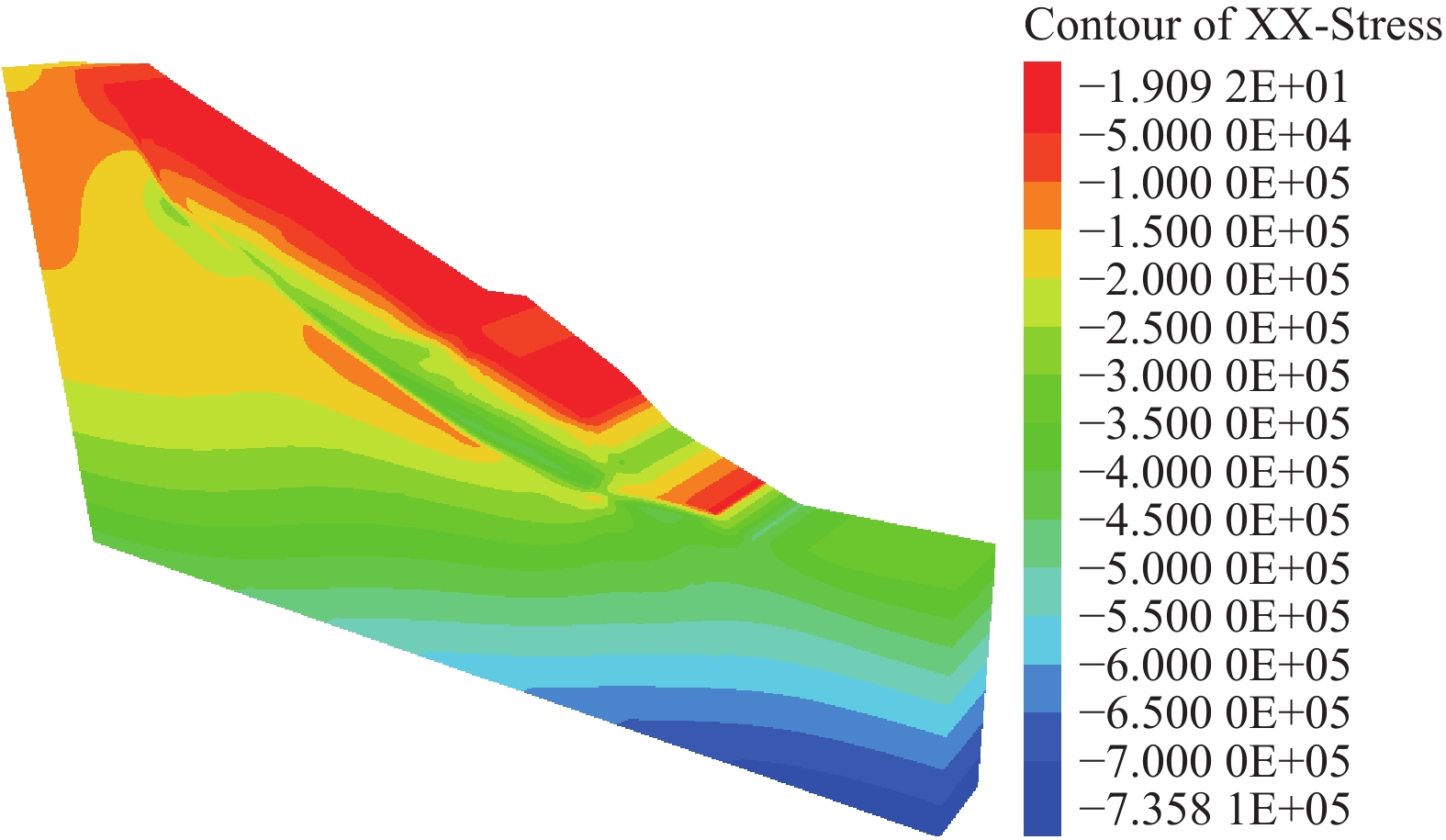
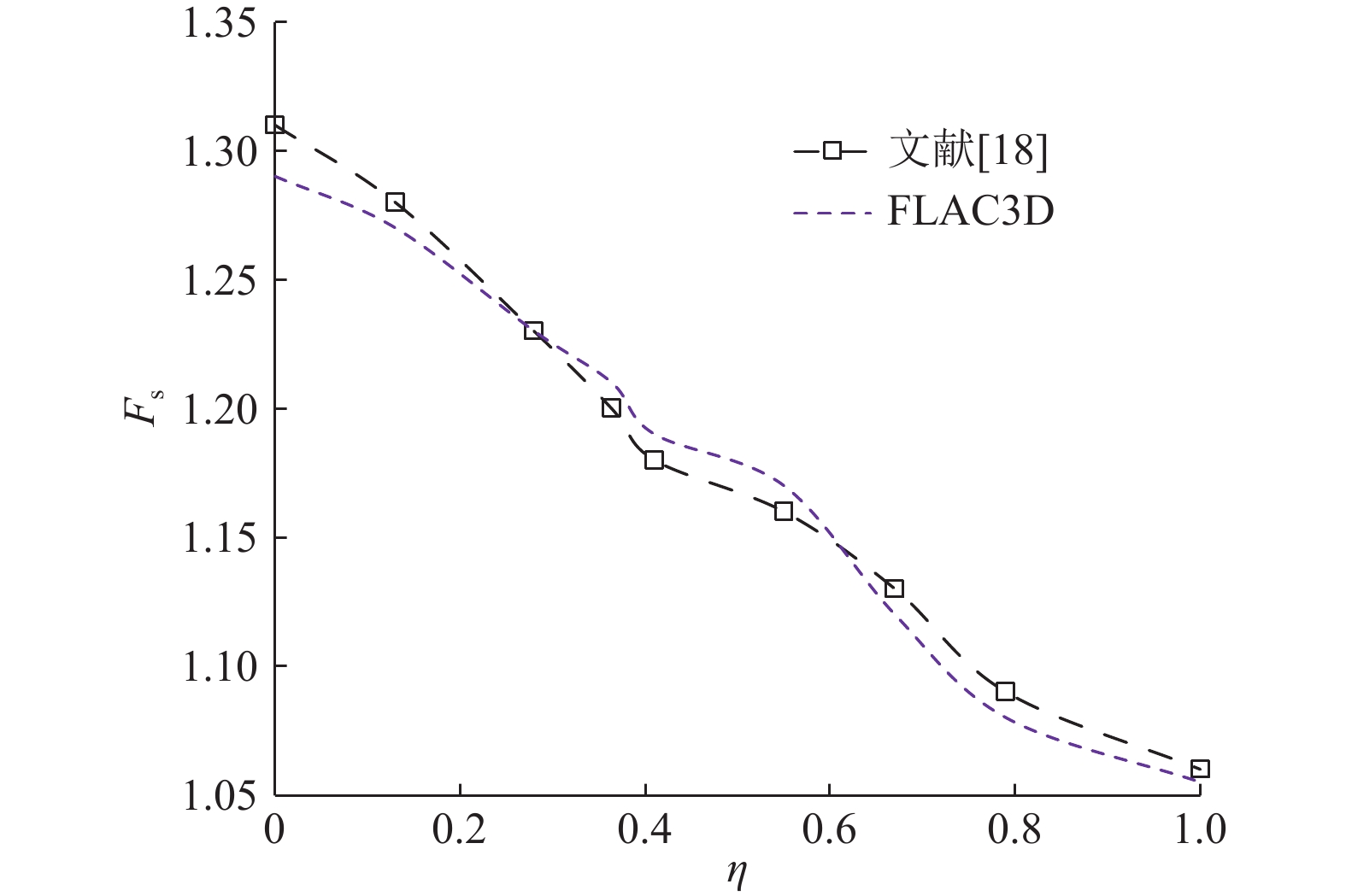
Abstract:Embedded piles act as an optimization structure compared with the traditional stabilizing pile. The determination of the thrust on the loading section is based mainly on the model test and numerical simulation, and there is a lack of in-depth theoretical analysis. For the bedrock-talus landslide reinforced by embedded piles, according to the potential overtop-sliding failure mode, the slide surface can be divided into top and bottom sections by the position of pile top, and the horizontal resultant force of the top section can be obtained by integration, which is the so-called thrust of the embedded section. Similarly, the force on the bottom section of the overtop-sliding surface can also be obtained. Based on the limit equilibrium theory, the force analysis of the sliding mass enclosed by the bottom sliding surface and the load section of the pile can be carried out, and the thrust on the loaded section can also be obtained. Example analyses show that the thrust of the embedded section and the loaded section obtained by the theoretical method are very consistent with the results of FLAC3D, the resultant force of the loading section decreases nonlinearly with the increase of the ratio, while the resultant force of the embedded section presents an opposite trend. With the increase of the embedded ratio from 0 to 0.67, the thrust ratio of embedded section and loading section increases slowly from 0 to 0.3−0.5. With the increase of embedded ratio from 0.67 to 0.8, the ratio increases sharply to 1.47−2.12. Generally, the thrust of embedded section is less than that of loaded section. The theoretical research of the thrust of the embedded pile is of great practical significance for the optimization of the pile internal force and the determination of the pile embedded depth, which will promote the further application of this structure.
-

-
表 1 抗滑桩及坡体主要物理力学参数
Table 1. Main physical and mechanical parameters of the landslide and piles
材料类型 土体重度
/(kN·m–3)黏聚力
/kPa内摩擦角
/(°)弹性模量
/MPa泊松比 碎石土 22 11 20.6 50 0.33 大理岩 23 450 37.0 600 0.25 抗滑桩 25 30 000 0.22 注:抗滑桩视为弹性体,故不考虑其黏聚力和内摩擦角。 -
[1] ITO T,MATSUI T,HONG W P. Design method for stabilizing piles against landslide: One row of piles[J]. Soils and Foundations,1981,21(1):21 − 37. doi: 10.3208/sandf1972.21.21
[2] RANDOLPH M F. The response of flexible piles to lateral loading[J]. Géotechnique,1981,31(2):247 − 259.
[3] 常晓军,葛伟亚,于洋,等. 福建省永泰县东门旗山滑坡诱发机理与防治措施[J]. 吉林大学学报(地球科学版),2019,49(4):1063 − 1072. [CHANG Xiaojun,GE Weiya,YU Yang,et al. Mechanism and mitigation measures of Qishan landslide of Yongtai in Fujian Province[J]. Journal of Jilin University (Earth Science Edition),2019,49(4):1063 − 1072. (in Chinese with English abstract)
[4] CHOW Y K. Analysis of piles used for slope stabilization[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1996,20(9):635 − 646. doi: 10.1002/(SICI)1096-9853(199609)20:9<635::AID-NAG839>3.0.CO;2-X
[5] HASSIOTIS S,CHAMEAU J L,GUNARATNE M. Design method for stabilization of slopes with piles[J]. Journal of Geotechnical and Geoenvironmental Engineering,1997,123(4):314 − 323. doi: 10.1061/(ASCE)1090-0241(1997)123:4(314)
[6] 郑颖人, 雷文杰, 赵尚毅, 等. 抗滑桩设计中的两个问题[J]. 公路交通科技, 2005, 22(增刊1): 45 − 51
ZHENG Yingren, LEI Wenjie, ZHAO Shangyi, et al. Two problems in design methods of anti-slide piles[J]. Journal of Highway and Transportation Research and Development, 2005, 22(Sup 1): 45 − 51. (in Chinese with English abstract)
[7] 闫玉平,肖世国. 双排抗滑桩加固滑坡的前桩后侧推力算法[J]. 水文地质工程地质,2021,48(4):55 − 63. [YAN Yuping,XIAO Shiguo. A calculation method for thrust on the fore piles of double-row stabilizing piles used to reinforce landslides[J]. Hydrogeology & Engineering Geology,2021,48(4):55 − 63. (in Chinese with English abstract)
[8] 王文沛,殷跃平,王立朝,等. 排水抗滑桩技术研究现状及展望[J]. 水文地质工程地质,2022,49(2):73 − 83. [WANG Wenpei,YIN Yueping,WANG Lichao,et al. Status and prospects of studies on anti-slide shaft technology[J]. Hydrogeology & Engineering Geology,2022,49(2):73 − 83. (in Chinese with English abstract)
[9] 向俐蓉,陈伟志,郭在旭,等. 大型滑坡抗滑桩-桩板结构受力变形研究[J]. 水文地质工程地质,2021,48(2):125 − 131. [XIANG Lirong,CHEN Weizhi,GUO Zaixu,et al. A study of the deformation of anti-slide pile and pile-plate structure in large landslide[J]. Hydrogeology & Engineering Geology,2021,48(2):125 − 131. (in Chinese with English abstract)
[10] 邓时容,肖世国. 嵌固段顶部拓宽型抗滑桩计算方法[J]. 中国地质灾害与防治学报,2022,33(4):84 − 91. [DENG Shirong,XIAO Shiguo. Calculation method of stabilizing piles with broadened top at the built-in section[J]. The Chinese Journal of Geological Hazard and Control,2022,33(4):84 − 91. (in Chinese with English abstract)
[11] 陶波,佴磊,伍法权,等. 论静止侧压力对抗滑桩的作用[J]. 吉林大学学报(地球科学版),2006,36(5):837 − 840. [TAO Bo,NAI Lei,WU Faquan,et al. The effect imposed on anti-slide pile by the static lateral pressure[J]. Journal of Jilin University (Earth Science Edition),2006,36(5):837 − 840. (in Chinese with English abstract)
[12] 肖世国. 考虑桩间土体抗滑作用的单排抗滑桩受力计算方法[J]. 中国地质灾害与防治学报,2020,31(1):89 − 94. [XIAO Shiguo. A calculation method for one row stabilizing piles considering resistance of soil between adjacent piles[J]. The Chinese Journal of Geological Hazard and Control,2020,31(1):89 − 94. (in Chinese with English abstract)
[13] POULOS H G. Design of reinforcing piles to increase slope stability[J]. Canadian Geotechnical Journal,1995,32(5):808 − 818. doi: 10.1139/t95-078
[14] 钟昌茂,邱恩喜,魏永幸,等. 基于桩体抗剪强度的复合地基路堤稳定性分析方法[J]. 水文地质工程地质,2020,47(5):100 − 107. [ZHONG Changmao,QIU Enxi,WEI Yongxing,et al. Stability analysis method for the composite foundation embankment based on pile shear strength[J]. Hydrogeology & Engineering Geology,2020,47(5):100 − 107. (in Chinese with English abstract)
[15] 任青阳,赵梦园,谢忠伟,等. 抗滑桩应变特征与内力非线性研究[J]. 水文地质工程地质,2021,48(2):114 − 124. [REN Qingyang,ZHAO Mengyuan,XIE Zhongwei,et al. A study of the strain characteristics and internal force nonlinearity of anti-slide pile[J]. Hydrogeology & Engineering Geology,2021,48(2):114 − 124. (in Chinese with English abstract)
[16] 李宁,刘冠麟,许建聪,等. 降雨条件下抗滑桩边坡三维稳定性分析[J]. 中国地质灾害与防治学报,2018,29(3):38 − 46. [LI Ning,LIU Guanlin,XU Jiancong,et al. 3D numerical analysis of the stability of a slope reinforced with piles under rainfall conditions[J]. The Chinese Journal of Geological Hazard and Control,2018,29(3):38 − 46. (in Chinese with English abstract)
[17] XIAO Shiguo. A simplified approach for stability analysis of slopes reinforced with one row of embedded stabilizing piles[J]. Bulletin of Engineering Geology and the Environment,2017,76(4):1371 − 1382. doi: 10.1007/s10064-016-0934-y
[18] YAN Yuping,XIAO Shiguo. A calculation method for the embedded depth of stabilizing piles in reinforced slopes[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2020,44(7):1077 − 1092. doi: 10.1002/nag.3052
[19] 熊治文. 深埋式抗滑桩的受力分布规律[J]. 中国铁道科学,2000,21(1):48 − 56. [XIONG Zhiwen. Force distribution rule of deeply buried anti slide pile[J]. China Railway Science,2000,21(1):48 − 56. (in Chinese with English abstract)
[20] 雷文杰, 郑颖人, 冯夏庭. 沉埋桩的有限元设计方法探讨[J]. 岩石力学与工程学报, 2006, 25(增刊1): 2924 − 2929
LEI Wenjie, ZHENG Yingren, FENG Xiating. Study on finite element design methods of slope stabilized by deeply buried anti-slide piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Sup 1): 2924 − 2929. (in Chinese with English abstract)
[21] 雷文杰,郑颖人,王恭先,等. 沉埋桩加固滑坡体模型试验的机制分析[J]. 岩石力学与工程学报,2007,26(7):1347 − 1355. [LEI Wenjie,ZHENG Yingren,WANG Gongxian,et al. Mechanism analysis of slope reinforcement with deeply buried piles with model test[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(7):1347 − 1355. (in Chinese with English abstract)
[22] 雷文杰,郑颖人,冯夏庭. 滑坡加固系统中沉埋桩的有限元极限分析研究[J]. 岩石力学与工程学报,2006,25(1):27 − 33. [LEI Wenjie,ZHENG Yingren,FENG Xiating. Limit analysis of slope stabilized by deeply buried piles with finite element method[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(1):27 − 33. (in Chinese with English abstract)
[23] 宋雅坤, 郑颖人, 雷文杰. 沉埋式抗滑桩机制模型试验数值分析研究[J]. 岩土力学, 2007, 28(增刊1): 63 − 68
SONG Yakun, ZHENG Yingren, LEI Wenjie. Analysis of the experimental mechanism of deeply buried anti-slide pile by FEM[J]. Rock and Soil Mechanics, 2007, 28(Sup1): 63 − 68. (in Chinese with English abstract)
[24] The MathWorks Inc. Global optimization toolbox: User’s guide (R2018b)[M/OL]. (2018-09-01)[2022-11-10]. http://www.mathworks.com/help/pdf doc/gads/gads tb.pdf.
[25] 徐邦栋. 滑坡分析与防治[M]. 北京: 中国铁道出版社, 2001
XU Bangdong. Landslide analysis and prevention[M]. Beijing: China Railway Publishing House, 2001. (in Chinese)
[26] 铁道部第二勘察设计院. 抗滑桩设计与计算[M]. 北京: 中国铁道出版社, 1983
The Second Survey and Design Institute of Ministry of Railways. Design and calculation of anti-slide pile[M]. Beijing: China Railway Publishing House, 1983. (in Chinese)
-



 下载:
下载: