力法计算锚索抗滑桩内力分担比及其应用

石洋海; 王贤能

doi:10.16031/j.cnki.issn.1003-8035.202202014

力法计算锚索抗滑桩内力分担比及其应用

深圳市工勘岩土集团有限公司, 广东深圳　518026

详细信息

作者简介: 石洋海（1984- ），男，硕士，高级工程师，主要从事地质灾害治理设计、岩土工程设计工作。E-mail：123889156@qq.com

中图分类号: P642.22

收稿日期: 2022-02-11

修回日期: 2022-05-31

刊出日期: 2022-08-25

Application of the structural mechanics method to calculate the internal force sharing ratio of anchor cable and anti-slide pile for retaining structure

Shenzhen Geokey Group Co. Ltd., Shenzhen, Guangdong　518026, China

Received Date: 11 February 2022

Revised Date: 31 May 2022

Publish Date: 25 August 2022

摘要

摘要:
锚索抗滑桩为常用的滑坡治理支护结构，抗滑桩锚固于滑动面以下岩土体中，锚索可视为多余约束，因此锚索抗滑桩为多次超静定结构。结构力学力法作为求解超静定结构的基本方法之一，以锚索拉力为基本未知量，综合考虑平衡条件、变形条件、物理条件求解锚索轴力，从而进一步确定锚索与抗滑桩各自分担的滑坡推力比例。文中以具体滑坡工程实例，采用力法求解锚索、抗滑桩结构内力，并建议锚索与抗滑桩的荷载分担比初步可按照30%～40%估算。
- 锚索 /
- 抗滑桩 /
- 荷载分担比 /
- 力法 /
- 不平衡推力法 /
- 剩余下滑力
Abstract:
The anchor cable anti-slip pile is a generally-used retaining structure for landslide control. The anchor cable is anchored in the rock mass below the sliding surface, so the anchor cable can be regarded as redundant constraint. Therefore, the anchor cable anti-slide pile are multiple statically indeterminate structures. As one of the basic methods for solving statically indeterminate structures, the structural mechanics force method takes anchor cable tension as the basic unknown quantity, through considering the balance condition, deformation condition and physical condition, the axial force of anchor cable was solved, and then the proportion of landslide thrust shared by anchor cable and anti-slide pile was further determined. In this paper, the structural mechanics method is used to solve the internal force of anchor cable and anti-slide pile, and it is suggested that the load sharing ratio between anchor cable and anti-slide pile can be estimated according to 30%~40%.
- anchor cable /
- anti-slide pile /
- load sharing ratio /
- the structural mechanics method /
- imbalance thrust force method /
- the residual landslide thrust

HTML全文

0. 引言

锚索抗滑桩为常用的滑坡治理支护结构，抗滑桩锚固于滑动面以下岩土体中，锚索支座可视为多余约束，因此锚索抗滑桩为多次超静定结构。力法作为求解超静定结构的基本方法之一，以锚索拉力为基本未知量，综合考虑平衡条件、变形条件、物理条件求解锚索轴力，从而进一步确定锚索与抗滑桩各自分担的滑坡推力比例。常规计算方法^[1]综合考虑锚索刚度、抗滑桩嵌固处的内力、角位移、线位移等多个参数，计算较复杂，不利于工程实际应用。文中结合滑坡治理工程实例，基于力法基本原理，对抗滑桩嵌固处的内力、变形、锚头位移进行合理简化，推导了锚索轴力简化计算公式，用于进一步求解桩锚内力分担比。

1. 力法求解锚索轴力的基本原理

1.1 基本假定

（1）抗滑桩上的滑坡推力呈矩形分布；

（2）抗滑桩桩前无可靠的支挡结构或滑动面以上土体较薄时，可不考虑桩前土体抗力作用；

（3）抗滑桩可视为嵌固于滑动面以下岩土体，抗滑桩在滑动面处无水平位移、转角位移；

（4）锚索张拉锁定时通过锚头卡紧抗滑桩，锚索自由段的弹性变形在张拉锁定时已消耗，锚头位置位移 ${\Delta _1} = {\Delta _2} = {\Delta _3} = 0$ ；

（5）抗滑桩前临空侧直立高度太大不利于滑坡稳定，假设锚索数量不大于3道。

1.2 力法典型方程及简化计算公式推导

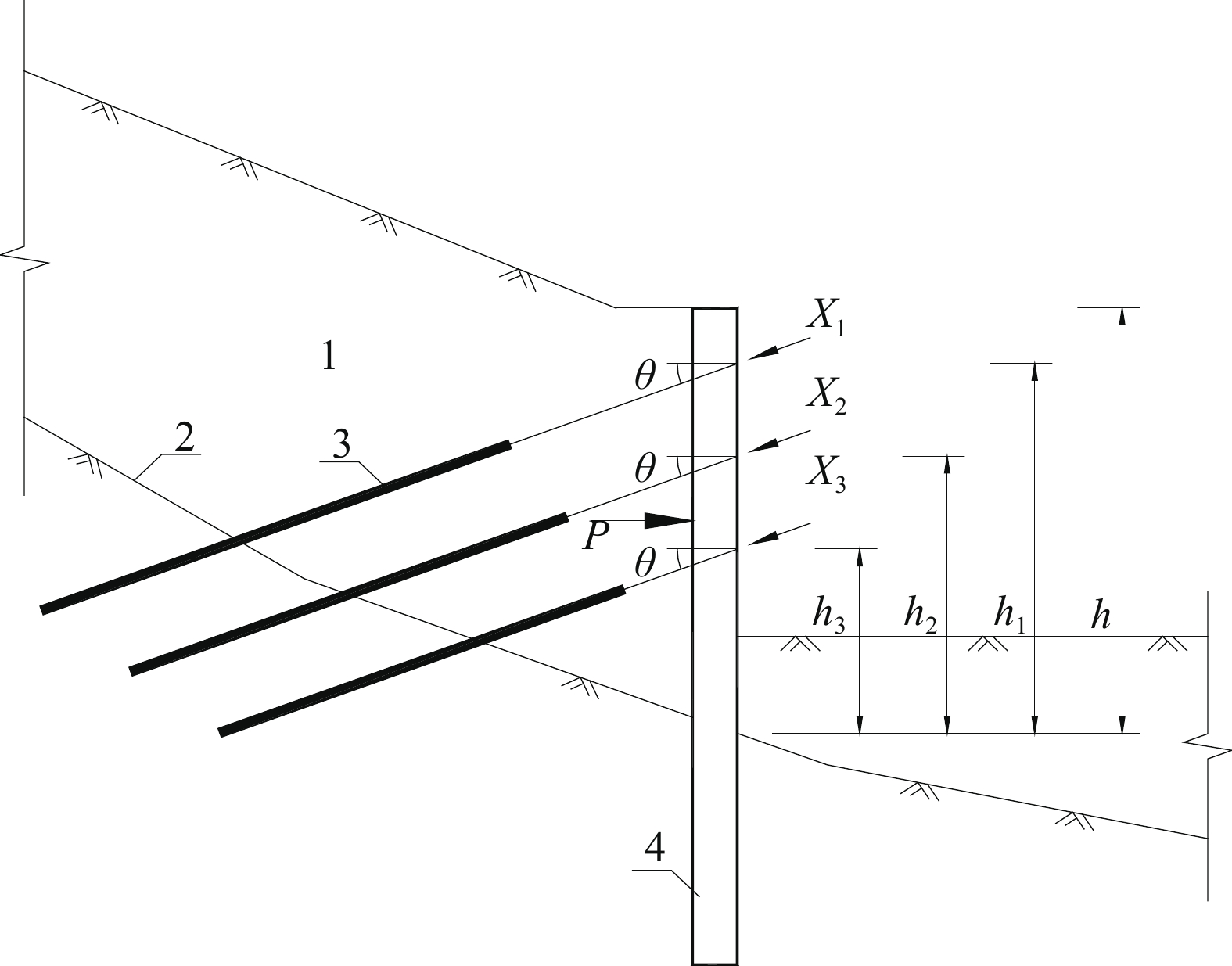
根据上述假设，锚索抗滑桩简化模型如图1所示，力法典型方程组如式（1）：

图 1. 锚索抗滑桩简化计算模型

注：图中

${X}_{1}、{X}_{2}、{X}_{3}$ 为第1、2、3道锚索轴向拉力，

${h}_{1}、{h}_{2}、{h}_{3}$ 为第1、2、3道锚索锚头距离滑动面的长度，P为滑坡推力，h为滑动面以上抗滑桩长度，1为滑坡体，2为滑动面，3为锚索锚固段，4为抗滑桩。

Figure 1. Simplified calculation model of anchor cable anti-slide pile

下载: 全尺寸图片幻灯片

$\left. \begin{gathered} {\Delta _1} = {\delta _{11}}{X_1}\cos \theta + {\delta _{12}}{X_2}\cos \theta + {\delta _{13}}{X_3}\cos \theta + {\Delta _{1P}} = 0 \\ {\Delta _2} = {\delta _{21}}{X_1}\cos \theta + {\delta _{22}}{X_2}\cos \theta + {\delta _{23}}{X_3}\cos \theta + {\Delta _{2P}} = 0 \\ {\Delta _3} = {\delta _{31}}{X_1}\cos \theta + {\delta _{32}}{X_2}\cos \theta + {\delta _{33}}{X_3}\cos \theta + {\Delta _{3P}} = 0 \\ \end{gathered} \right\}$

(1)

式中： ${\delta _{ii}}——$ 多余未知力 $\overline {{X_i}} = 1$ 单独作用时引起的沿其本身方向上的位移；

${\delta _{ij}}——$ 多余未知力 $\overline {{X_j}} = 1$ 单独作用时引起的沿 ${X_i}$ 方向上的位移；

${\Delta _{iP}}——$ 荷载P单独作用时引起的沿 ${X_i}$ 方向上的位移。

应用图乘法求得力法方程组中的主系数、副系数、自由项系数分别如式（2）—（10）：

$\begin{split} {\delta _{11}} &= \sum {\int {\frac{{\overline {{M_1}} \overline {{M_1}} {d_s}}}{{EI}}} } = \frac{1}{{EI}}\left( {\frac{1}{2}{h_1} \cdot {h_1}\cos \theta } \right) \cdot \left( {\frac{2}{3}{h_1}\cos \theta } \right) \\ &= \frac{{h_1^3{{\cos }^2}\theta }}{{3EI}} \end{split}$

(2)

$\begin{split} {\delta _{22}} &= \sum {\int {\frac{{\overline {{M_2}} \overline {{M_2}} {d_s}}}{{EI}}} } = \frac{1}{{EI}}\left( {\frac{1}{2}{h_2} \cdot {h_2}\cos \theta } \right) \cdot \left( {\frac{2}{3}{h_2}\cos \theta } \right) \\ &= \frac{{h_2^3{{\cos }^2}\theta }}{{3EI}} \end{split}$

(3)

$\begin{split} {\delta _{33}} &= \sum {\int {\frac{{\overline {{M_3}} \overline {{M_3}} {d_s}}}{{EI}}} } = \frac{1}{{EI}}\left( {\frac{1}{2}{h_3} \cdot {h_3}\cos \theta } \right) \cdot \left( {\frac{2}{3}{h_3}\cos \theta } \right) \\ &= \frac{{h_3^3{{\cos }^2}\theta }}{{3EI}} \end{split}$

(4)

${\delta }_{12}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{1}}\overline{{M}_{2}}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{2}{h}_{1}\cdot {h}_{1}\mathrm{cos}\theta \right)\cdot \left(\frac{{h}_{2}-{h}_{1}/3}{{h}_{2}}{h}_{2}\mathrm{cos}\theta \right)=\frac{{h}_{1}{}^{2}{\mathrm{cos}}^{2}\theta }{2EI}\cdot \left({h}_{2}-\frac{{h}_{1}}{3}\right)$

(5)

${\delta }_{23}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{2}}\overline{{M}_{3}}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{2}{h}_{3}\cdot {h}_{3}\mathrm{cos}\theta \right)\cdot \left(\frac{{h}_{2}-{h}_{3}/3}{{h}_{2}}{h}_{2}\mathrm{cos}\theta \right)=\frac{{h}_{3}{}^{2}{\mathrm{cos}}^{2}\theta }{2EI}\cdot \left({h}_{2}-\frac{{h}_{3}}{3}\right)$

(6)

${\delta }_{13}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{1}}\overline{{M}_{3}}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{2}{h}_{3}\cdot {h}_{3}\mathrm{cos}\theta \right)\cdot \left(\frac{{h}_{1}-{h}_{3}/3}{{h}_{1}}{h}_{1}\mathrm{cos}\theta \right)=\frac{{h}_{3}{}^{2}{\mathrm{cos}}^{2}\theta }{2EI}\cdot \left({h}_{1}-\frac{{h}_{3}}{3}\right)$

(7)

${\Delta }_{1P}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{1}}{M}_{P}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{3}\cdot \frac{1}{2}Ph\cdot h\right)\cdot \left(\frac{{h}_{1}-h/4}{{h}_{1}}{h}_{1}\mathrm{cos}\theta \right)=\frac{P{h}^{2}\mathrm{cos}\theta }{6EI}\cdot \left({h}_{1}-\frac{h}{4}\right)$

(8)

${\Delta }_{2P}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{2}}{M}_{P}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{3}\cdot \frac{1}{2}Ph\cdot h\right)\cdot \left(\frac{{h}_{2}-h/4}{{h}_{2}}{h}_{2}\mathrm{cos}\theta \right)=\frac{P{h}^{2}\mathrm{cos}\theta }{6EI}\cdot\left({h}_{2}-\frac{h}{4}\right)$

(9)

${\Delta }_{3P}={\displaystyle \sum {\displaystyle \int \frac{\overline{{M}_{3}}{M}_{P}{d}_{s}}{EI}}}=\frac{1}{EI}\left(\frac{1}{3}\cdot \frac{1}{2}Ph\cdot h\right)\cdot \left(\frac{{h}_{3}-h/4}{{h}_{3}}{h}_{3}\mathrm{cos}\theta \right)=\frac{P{h}^{2}\mathrm{cos}\theta }{6EI}\cdot \left({h}_{3}-\frac{h}{4}\right)$

(10)

式中：M——弯矩；

d_s——积分因子；

EI——抗弯刚度；

h₁、h₂、h₃、θ——见图1。

将上述主系数、副系数、自由项系数式（2）—（10）代入力法方程组（1）并求解，得到锚索拉力分别如式（11）—（13）：

${X_1}\cos \theta = \frac{{({\delta _{23}}{\Delta _{1P}} - {\delta _{12}}{\Delta _{3P}})({\delta _{13}}{\delta _{22}} - {\delta _{12}}{\delta _{23}}) - ({\delta _{22}}{\Delta _{1P}} - {\delta _{12}}{\Delta _{2P}})({\delta _{13}}{\delta _{23}} - {\delta _{12}}{\delta _{33}})}}{{({\delta _{11}}{\delta _{22}} - {\delta _{12}}{\delta _{12}})({\delta _{13}}{\delta _{23}} - {\delta _{12}}{\delta _{33}}) - ({\delta _{11}}{\delta _{23}} - {\delta _{12}}{\delta _{13}})({\delta _{13}}{\delta _{22}} - {\delta _{12}}{\delta _{23}})}}$

(11)

${X_2}\cos \theta = \frac{{({\delta _{13}}{\Delta _{1P}} - {\delta _{11}}{\Delta _{3P}})({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}}) - ({\delta _{12}}{\Delta _{1P}} - {\delta _{11}}{\Delta _{2P}})({\delta _{13}}{\delta _{13}} - {\delta _{11}}{\delta _{33}})}}{{({\delta _{12}}{\delta _{12}} - {\delta _{11}}{\delta _{12}})({\delta _{13}}{\delta _{13}} - {\delta _{11}}{\delta _{33}}) - ({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}})({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}})}}$

(12)

${X_3}\cos \theta = \frac{{({\delta _{13}}{\Delta _{1P}} - {\delta _{11}}{\Delta _{3P}})({\delta _{12}}{\delta _{12}} - {\delta _{11}}{\delta _{12}}) - ({\delta _{12}}{\Delta _{1P}} - {\delta _{11}}{\Delta _{2P}})({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}})}}{{({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}})({\delta _{12}}{\delta _{13}} - {\delta _{11}}{\delta _{23}}) - ({\delta _{13}}{\delta _{13}} - {\delta _{11}}{\delta _{23}})({\delta _{12}}{\delta _{12}} - {\delta _{11}}{\delta _{12}})}}$

(13)

1.3 滑坡推力计算

对于折线型滑动面，采用不平衡推力传递法^[2-4]计算剩余下滑力。

2. 工程实例分析

2.1 工程概况

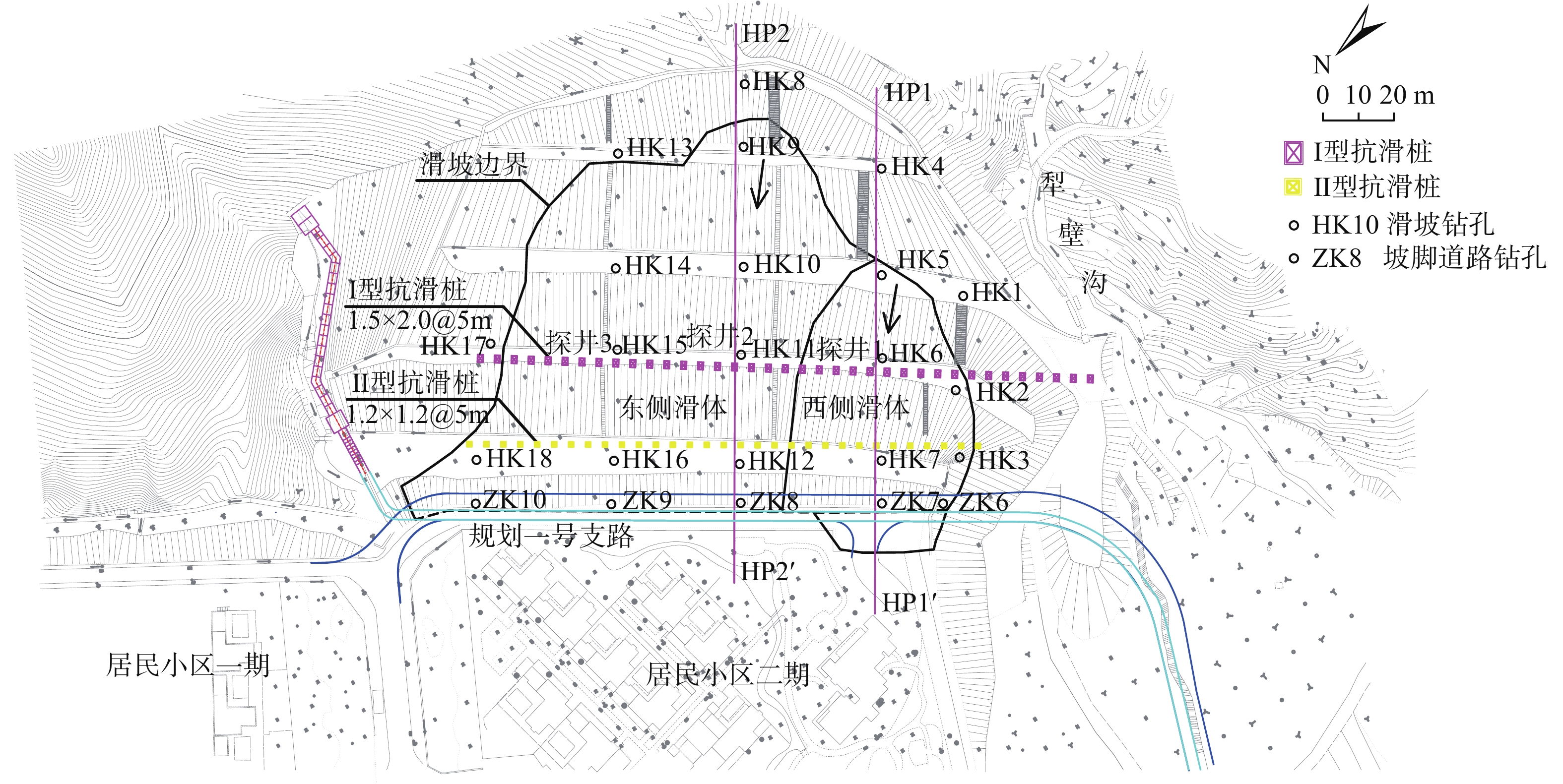
2018年8月，深圳市某山体发生滑坡，坡脚为住宅小区及拟建市政道路、坡顶为自然山体。该滑坡为土质滑坡，滑坡平面形态呈不规则半圆形，主滑方向NE31°，滑坡区宽65～165 m、纵长80～110m，平面面积约1.3×10⁴ m²，厚度5.5～10 m，平均厚度6.3 m，滑坡总体积14.3×10⁴ m³，属于中层特大型滑坡。

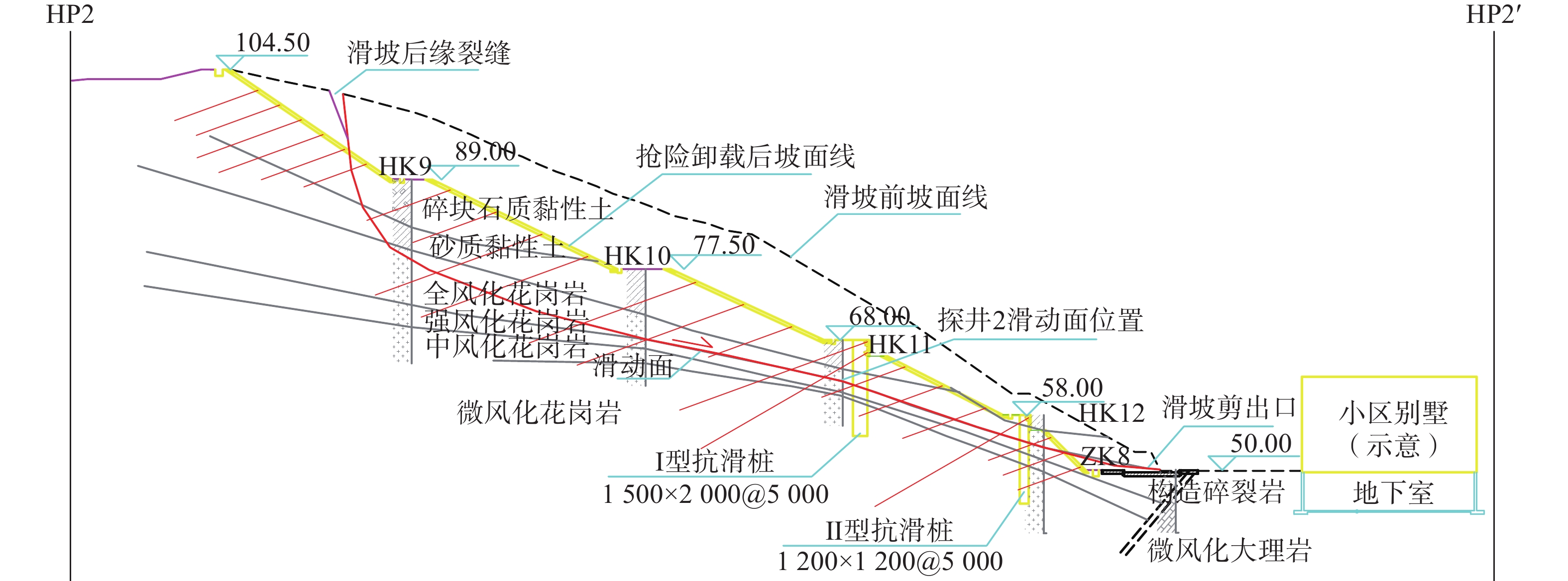
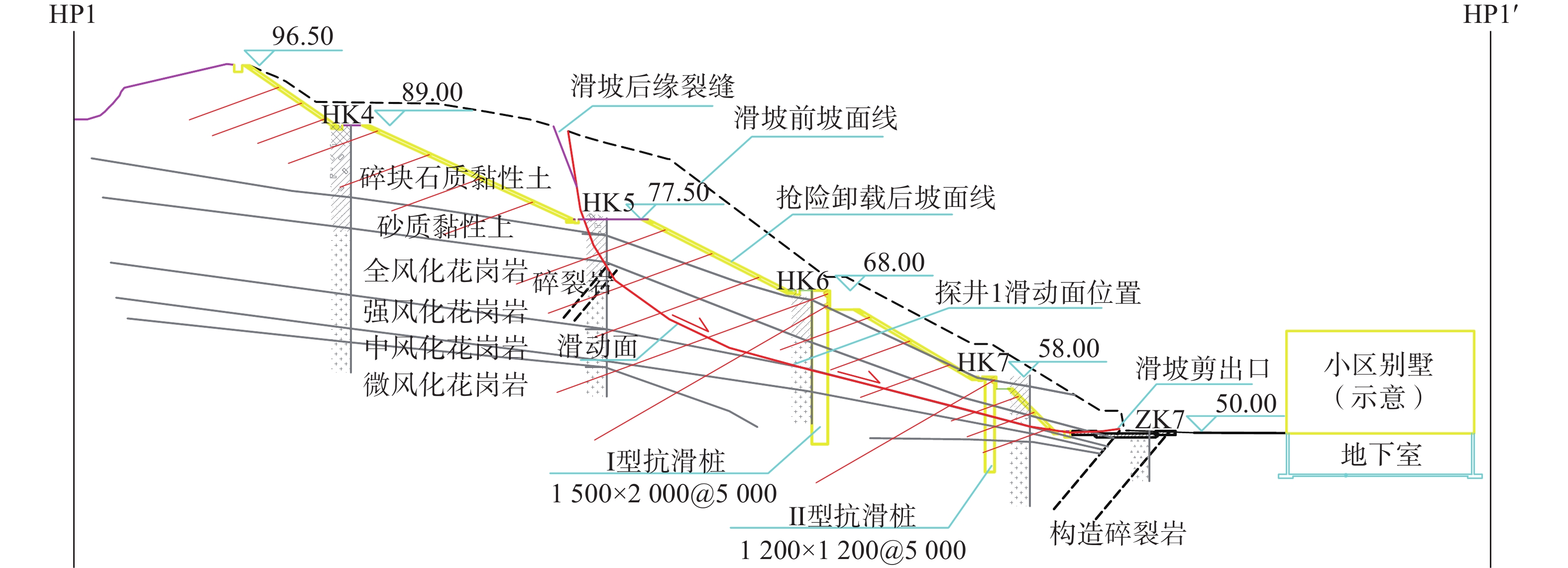
滑坡抢险阶段分级削坡以卸除部分滑体，滑坡永久性治理措施为：在第二级边坡平台设置1500×2000@5000抗滑桩+两道锚索，在第一级边坡平台设置1200×1200@5000抗滑桩+一道锚索。滑坡治理平面图、典型剖面图如图2—4所示。

图 2. 滑坡治理平面图

Figure 2. The plane graph of landslide strengthening

下载: 全尺寸图片幻灯片

图 4. HP2—HP2′主滑剖面简图

Figure 4. Sketch of HP2—HP2′ main slide section

下载: 全尺寸图片幻灯片

图 3. HP1—HP1′主滑剖面简图

Figure 3. Sketch of HP1—HP1′ main slide section

下载: 全尺寸图片幻灯片

2.2 计算参数

滑动面参数采用反算确定，反算坡面还原至滑坡前原始地面线，以滑体处于极限状态作为反演条件。参数分析时土体饱和重度取γ=19 kN/m³，c=9～18 kPa，φ=9°～18°，假设滑坡临界状态瞬时稳定性系数为0.95。经反算，主滑剖面抗剪强度参数反算结果为c=14 kPa，φ=12.2°。

2.3 计算过程

2.3.1 主滑剖面条块下滑力计算

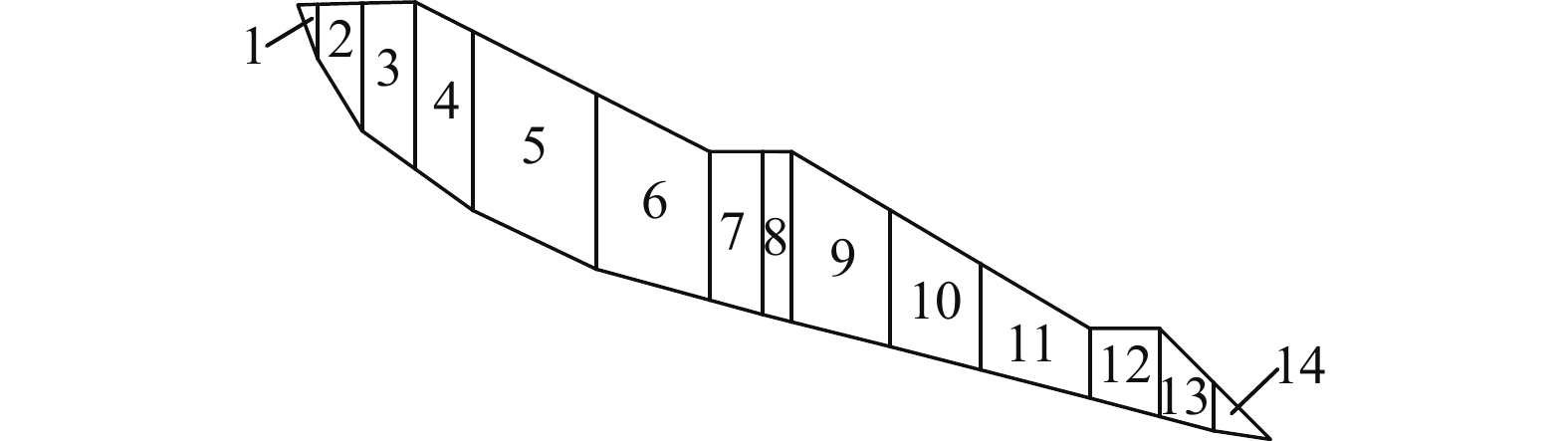
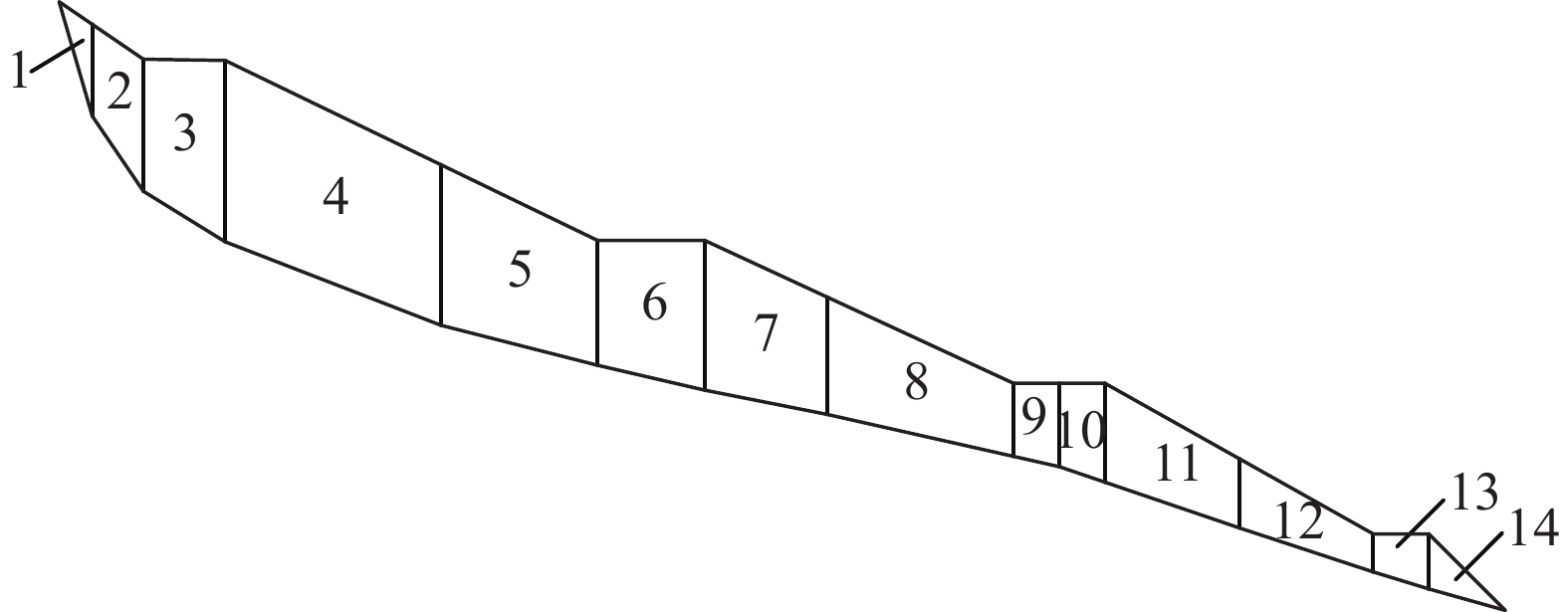
（1）HP1—HP1′主滑剖面计算条块图如图5所示，其中第7条块的剩余下滑力为Ⅰ型抗滑桩桩后条块下滑力，计算值为814.34 kN/m；第11条块的剩余下滑力为Ⅱ型抗滑桩桩后条块下滑力，计算值为161.32 kN/m。

图 5. HP1—HP1′主滑剖面计算条块图

Figure 5. The calculate block of HP1—HP1′ main slide section

下载: 全尺寸图片幻灯片

（2）HP2—HP2′主滑剖面计算条块图如图6所示，其中第9条块的剩余下滑力为Ⅰ型抗滑桩桩后条块下滑力，计算值为596.45 kN/m；第12条块的剩余下滑力为Ⅱ型抗滑桩桩后条块下滑力，计算值为172.41 kN/m。

图 6. HP2—HP2′主滑剖面计算条块图

Figure 6. The calculate block of HP2—HP2′ main slide section

下载: 全尺寸图片幻灯片

2.3.2 主滑剖面桩前抗力计算

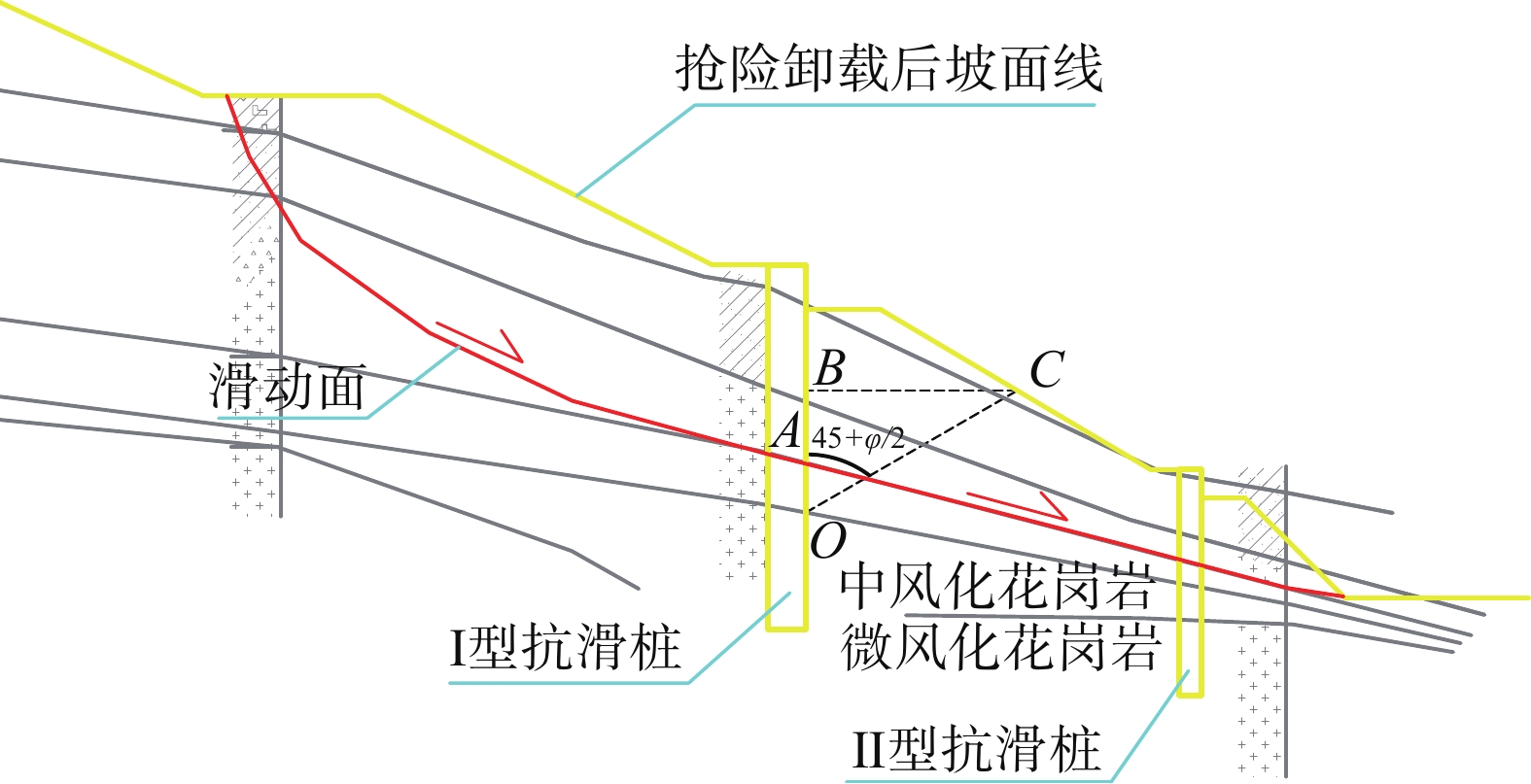
本滑坡治理采用Ⅰ型、Ⅱ型共两排抗滑桩，其中Ⅰ型抗滑桩由于桩前土体受到Ⅱ型抗滑桩的支挡作用，可考虑相应的抗力，Ⅱ型抗滑桩桩前为临空侧，不考虑相应的抗力。以HP1—HP1′主滑动面为例，Ⅰ型抗滑桩桩前土体抗力计算简图如图7所示，图中 $\angle BOC$ =45°+φ/2，AB段为桩前土体被动土压力计算高度，由于AB段位于滑坡体内，计算桩前抗力时可按照1/3～2/3的系数折减^[5-8]。

图 7. Ⅰ型抗滑桩桩前土体抗力计算简图

注：图中O为Ⅰ型抗滑桩与中风化岩面交点，A为Ⅰ型抗滑桩与滑动面的交点，C为计算破裂面与坡面的交点，B为C点在Ⅰ型抗滑桩上的投影。

Figure 7. Schematic diagram of soil resistance in front of type Ⅰ anti-slide pile

下载: 全尺寸图片幻灯片

2.3.3 主滑剖面剩余下滑力计算

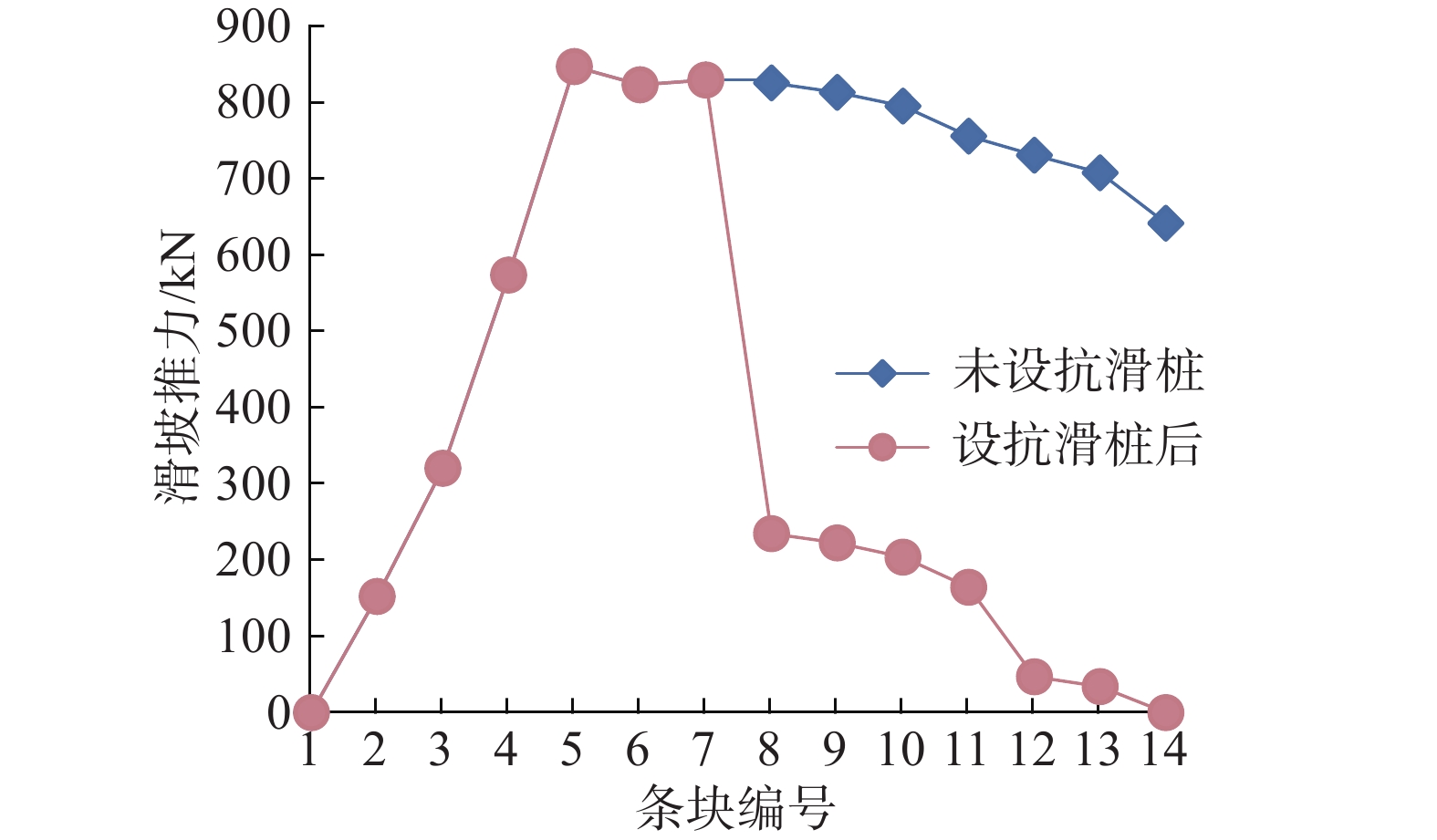
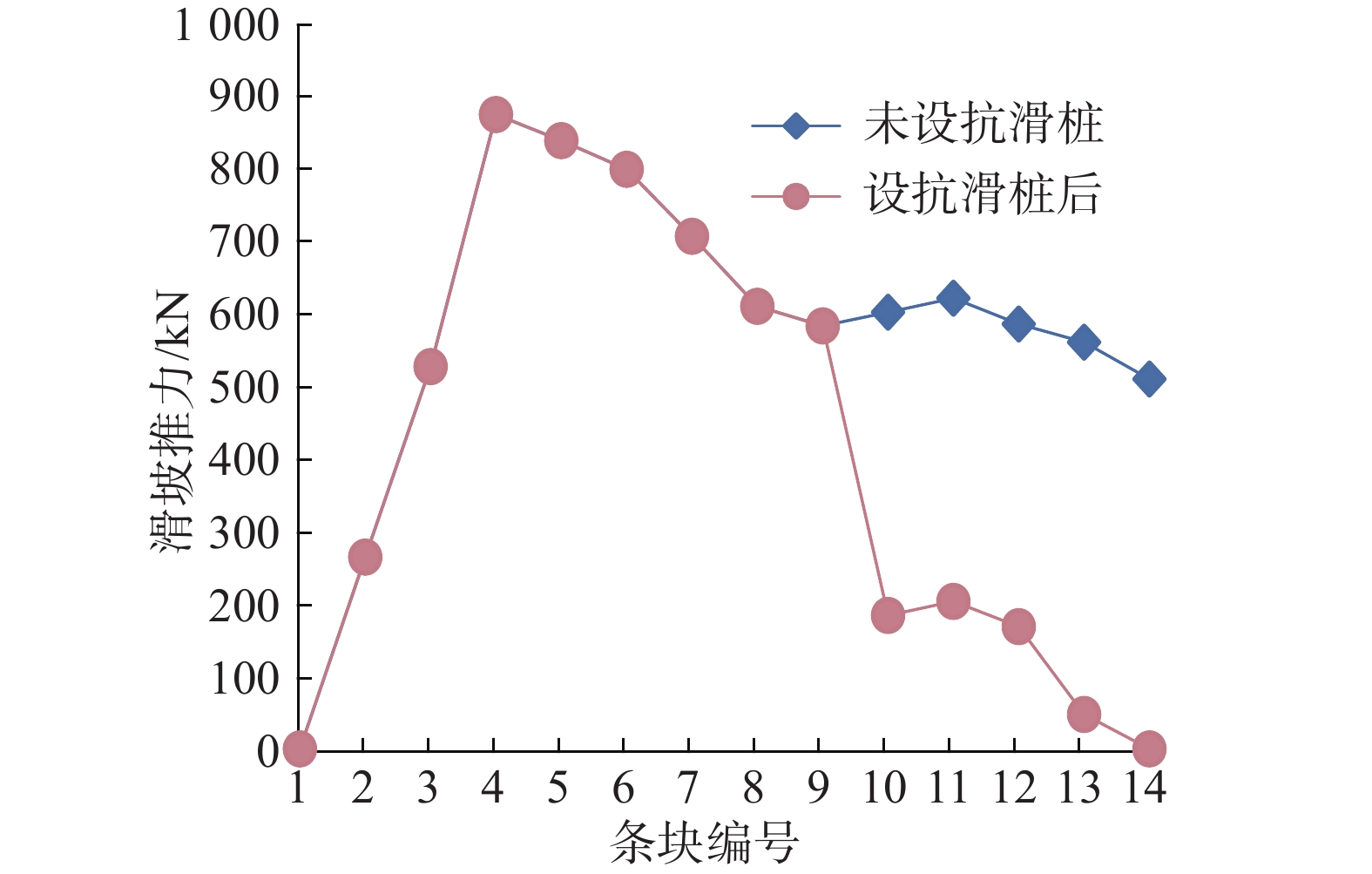
采用不平衡推力法计算并考虑Ⅰ型抗滑桩桩前土体抗力后，滑坡典型剖面下滑力计算结果分别如图8、图9所示，抗滑桩处剩余下滑力计算结果如表1所示。

图 8. HP1—HP1′剖面条块下滑力

Figure 8. The block sliding force of HP1—HP1′ section

下载: 全尺寸图片幻灯片

图 9. HP2—HP2′剖面条块下滑力

Figure 9. The block sliding force of HP2—HP2′ section

下载: 全尺寸图片幻灯片

表 1. 抗滑桩处剩余下滑力计算结果

Table 1. Calculation results of the residual landslide thrust at anti-slide pile

	Ⅰ型抗滑桩（后排）				Ⅱ型抗滑桩（前排）
主轴断面	桩后条块下滑力 /kN	桩前抗力 /kN	剩余下滑力 /kN	前后排桩分担比 /%	桩后条块下滑力 /kN	桩前抗力 /kN	剩余下滑力 /kN	前后排桩分担比 /%
HP1—HP1′	814.34	154.26	660.08	80.4	161.32	0	161.32	19.6
HP2—HP2′	596.45	116.82	479.63	73.6	172.41	0	172.41	26.4

| Show Table

DownLoad: CSV

经计算，HP1—HP1′剖面Ⅰ型抗滑桩处剩余下滑力为660.08 kN，Ⅱ型抗滑桩处剩余下滑力为161.32 kN；Ⅰ型、Ⅱ型抗滑桩处剩余下滑力占比分别为80.4%、19.6%。

HP2—HP2′剖面Ⅰ型抗滑桩处剩余下滑力为479.63 kN，Ⅱ型抗滑桩处剩余下滑力为172.41 kN；Ⅰ型、Ⅱ型抗滑桩处剩余下滑力占比分别为73.6%、26.4%。

2.4 计算结果与分析

本滑坡治理工程实例中，Ⅰ型抗滑桩桩身设置两道锚索，Ⅱ型抗滑桩桩身设置一道锚索。表1中得到的剩余下滑力由抗滑桩与锚索共同承担，将主滑剖面相应的距离、角度代入上述公式即可求得相应的锚索荷载分担比，结果如表2所示。

表 2. 抗滑桩桩身锚索荷载分担比

Table 2. The load sharing ratio of anchor cable in anti-slide pile

	Ⅰ型抗滑桩（后排）				Ⅱ型抗滑桩（前排）
主滑剖面	剩余下滑力 P/（kN·m⁻¹）	锚索水平力X₁·cosθ/（kN·m⁻¹）	锚索水平力X₂·cosθ/（kN·m⁻¹）	锚索轴力占比/%	剩余下滑力 P/（kN·m⁻¹）	锚索水平力X₁·cosθ/（kN·m⁻¹）	锚索轴力占比/%
HP1—HP1′	660.08	123.17	109.18	35.2	161.32	62.26	38.6
HP2—HP2′	479.63	98.62	80.76	37.4	172.41	67.58	39.2

| Show Table

DownLoad: CSV

本滑坡治理工程中，抗滑桩、锚索间距均为5 m，Ⅰ型抗滑桩锚索倾角θ=20°，Ⅱ型抗滑桩锚索倾角θ=30°，锚索轴向力结果如表3所示。

表 3. 抗滑桩桩身锚索轴力计算结果

Table 3. Anchor cable calculation results of axial force in anti-slide pile

	Ⅰ型抗滑桩		Ⅱ型抗滑桩
主滑剖面	锚索轴向力 X₁/kN	锚索轴向力 X₂/kN	锚索轴向力 X₁/kN
HP1—HP1′	655.4	580.9	360
HP2—HP2′	524	430	390

| Show Table

DownLoad: CSV

3. 结论

（1）通过结构力学力法，把锚索锚头视为多余约束，可将锚索抗滑桩简化为静定结构求解内力；

（2）本滑坡实例中，HP1—HP1′剖面Ⅰ型、Ⅱ型抗滑桩处剩余下滑力占比分别为80.4%、19.6%，HP2—HP2′剖面Ⅰ型、Ⅱ型抗滑桩处剩余下滑力占比分别为73.6%、26.4%。Ⅰ型抗滑桩（后排）承担70%～80%的剩余下滑力；

（3）锚索所承担Ⅰ型、Ⅱ型抗滑桩计算条块相应剩余下滑力的比例，HP1—HP1′剖面分别为35.2%、38.6%，HP2—HP2′剖面分别为37.4%、39.2%。该比例与滑坡体岩土性质、滑坡推力布置形式、锚索数量及间距等因素相关，初步可按照30%～40%进行估算。

图 1 锚索抗滑桩简化计算模型

Figure 1.

下载: 全尺寸图片幻灯片

图 2 滑坡治理平面图

Figure 2.

下载: 全尺寸图片幻灯片

图 4 HP2—HP2′主滑剖面简图

Figure 4.

下载: 全尺寸图片幻灯片

图 3 HP1—HP1′主滑剖面简图

Figure 3.

下载: 全尺寸图片幻灯片

图 5 HP1—HP1′主滑剖面计算条块图

Figure 5.

下载: 全尺寸图片幻灯片

图 6 HP2—HP2′主滑剖面计算条块图

Figure 6.

下载: 全尺寸图片幻灯片

图 7 Ⅰ型抗滑桩桩前土体抗力计算简图

Figure 7.

下载: 全尺寸图片幻灯片

图 8 HP1—HP1′剖面条块下滑力

Figure 8.

下载: 全尺寸图片幻灯片

图 9 HP2—HP2′剖面条块下滑力

Figure 9.

下载: 全尺寸图片幻灯片

表 1 抗滑桩处剩余下滑力计算结果

Table 1. Calculation results of the residual landslide thrust at anti-slide pile

	Ⅰ型抗滑桩（后排）				Ⅱ型抗滑桩（前排）
主轴断面	桩后条块下滑力 /kN	桩前抗力 /kN	剩余下滑力 /kN	前后排桩分担比 /%	桩后条块下滑力 /kN	桩前抗力 /kN	剩余下滑力 /kN	前后排桩分担比 /%
HP1—HP1′	814.34	154.26	660.08	80.4	161.32	0	161.32	19.6
HP2—HP2′	596.45	116.82	479.63	73.6	172.41	0	172.41	26.4

下载: 导出CSV

表 2 抗滑桩桩身锚索荷载分担比

Table 2. The load sharing ratio of anchor cable in anti-slide pile

	Ⅰ型抗滑桩（后排）				Ⅱ型抗滑桩（前排）
主滑剖面	剩余下滑力 P/（kN·m⁻¹）	锚索水平力X₁·cosθ/（kN·m⁻¹）	锚索水平力X₂·cosθ/（kN·m⁻¹）	锚索轴力占比/%	剩余下滑力 P/（kN·m⁻¹）	锚索水平力X₁·cosθ/（kN·m⁻¹）	锚索轴力占比/%
HP1—HP1′	660.08	123.17	109.18	35.2	161.32	62.26	38.6
HP2—HP2′	479.63	98.62	80.76	37.4	172.41	67.58	39.2

下载: 导出CSV

表 3 抗滑桩桩身锚索轴力计算结果

Table 3. Anchor cable calculation results of axial force in anti-slide pile

	Ⅰ型抗滑桩		Ⅱ型抗滑桩
主滑剖面	锚索轴向力 X₁/kN	锚索轴向力 X₂/kN	锚索轴向力 X₁/kN
HP1—HP1′	655.4	580.9	360
HP2—HP2′	524	430	390

下载: 导出CSV

参考文献(8)

[1]	国家市场监督管理总局, 国家标准化管理委员会. 滑坡防治设计规范: GB/T 38509—2020[S]. 北京: 中国标准出版社, 2020 The State Administration for Market Regulation, Standardization Administration of the People's Republic of China. Code for the design of landslide stabilization: GB/T 38509—2020[S]. Beijing: Standards Press of China, 2020. （in Chinese）
[2]	中华人民共和国住房和城乡建设部. 建筑边坡工程技术规范: GB 50330—2013[S]. 北京: 中国建筑工业出版社, 2014 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical code for building slope engineering: GB 50330—2013[S]. Beijing: China Architecture & Building Press, 2014. （in Chinese）
[3]	肖世国. 考虑桩间土体抗滑作用的单排抗滑桩受力计算方法[J]. 中国地质灾害与防治学报,2020,31(1):89 − 94. [XIAO Shiguo. A calculation method for one row stabilizing piles considering resistance of soil between adjacent piles[J]. The Chinese Journal of Geological Hazard and Control,2020,31(1):89 − 94. (in Chinese with English abstract)
[4]	徐青,刘红宇,王一凡. 抗滑桩设计推力计算研究[J]. 武汉大学学报(工学版),2021,54(6):488 − 493. [XU Qing,LIU Hongyu,WANG Yifan. Study on design thrust force for anti-slide piles[J]. Engineering Journal of Wuhan University,2021,54(6):488 − 493. (in Chinese with English abstract)
[5]	闫玉平,肖世国. 双排抗滑桩加固滑坡的前桩后侧推力算法[J]. 水文地质工程地质,2021,48(4):55 − 63. [YAN Yuping,XIAO Shiguo. A calculation method for thrust on the fore piles of double-row stabilizing piles used to reinforce landslides[J]. Hydrogeology & Engineering Geology,2021,48(4):55 − 63. (in Chinese with English abstract)
[6]	上官力,马显春,肖洋. 高陡堆积体滑坡半坡桩无效锚固深度分析[J]. 中国地质灾害与防治学报,2019,30(4):69 − 75. [SHANGGUAN Li,MA Xianchun,XIAO Yang. Analysis on the invalid anchorage depth of hemi-slope anti-slide pile in high and steep colluvium landslide[J]. The Chinese Journal of Geological Hazard and Control,2019,30(4):69 − 75. (in Chinese with English abstract)
[7]	周云涛,石胜伟,蔡强,等. 预应力锚索修复变形抗滑桩模型试验与数值模拟分析[J]. 中国地质灾害与防治学报,2020,31(3):58 − 64. [ZHOU Yuntao,SHI Shengwei,CAI Qiang,et al. Numerical analysis and model test of deformed anti-sliding pile repaired by anchor cable[J]. The Chinese Journal of Geological Hazard and Control,2020,31(3):58 − 64. (in Chinese with English abstract)
[8]	徐根连,贺荣华,郭定国,等. 锚拉或刚架抗滑桩计算的解析和数值方法[J]. 工程勘察,2020,48(7):32 − 40. [XU Genlian,HE Ronghua,GUO Dingguo,et al. Analytical and numerical method for the calculation of anti-slide pile with anchor or rigid frame[J]. Geotechnical Investigation & Surveying,2020,48(7):32 − 40. (in Chinese with English abstract)

施引文献

期刊类型引用(4)

1.	丁选明，刘学成，王春艳，任寄瑜，刘诗敏. ECC桩-消能锚韧性支挡结构的地震响应规律. 土木与环境工程学报(中英文). 2025(02): 76-88 . 百度学术
2.	侯小强，王新飞，贾洪璐，安玉科，周重任，侯云龙. 渐进式滑坡锚索抗滑桩预应力张拉值计算. 工程科学与技术. 2024(01): 138-147 . 百度学术
3.	黎俊杰，肖世国. 穿坡油气管道的框架桩防护结构分析方法. 吉林大学学报(地球科学版). 2024(05): 1615-1628 . 百度学术
4.	段鹏. 支挡结构在崩塌、滑坡地质灾害治理中的应用. 华北自然资源. 2023(02): 102-105 . 百度学术

其他类型引用(0)

资源附件(0)

访问统计

图(9)

表(3)

计量

文章访问数: 971
PDF下载数: 67
施引文献: 4

0. 引言
1. 力法求解锚索轴力的基本原理
1.1 基本假定
1.2 力法典型方程及简化计算公式推导
1.3 滑坡推力计算
2. 工程实例分析
2.1 工程概况
2.2 计算参数
2.3 计算过程
2.4 计算结果与分析
3. 结论

力法计算锚索抗滑桩内力分担比及其应用

深圳市工勘岩土集团有限公司, 广东 深圳 518026

作者简介: 石洋海（1984- ），男，硕士，高级工程师，主要从事地质灾害治理设计、岩土工程设计工作。E-mail：123889156@qq.com