A controlled beam migration for anisotropic media and its application to marine data
-
摘要:
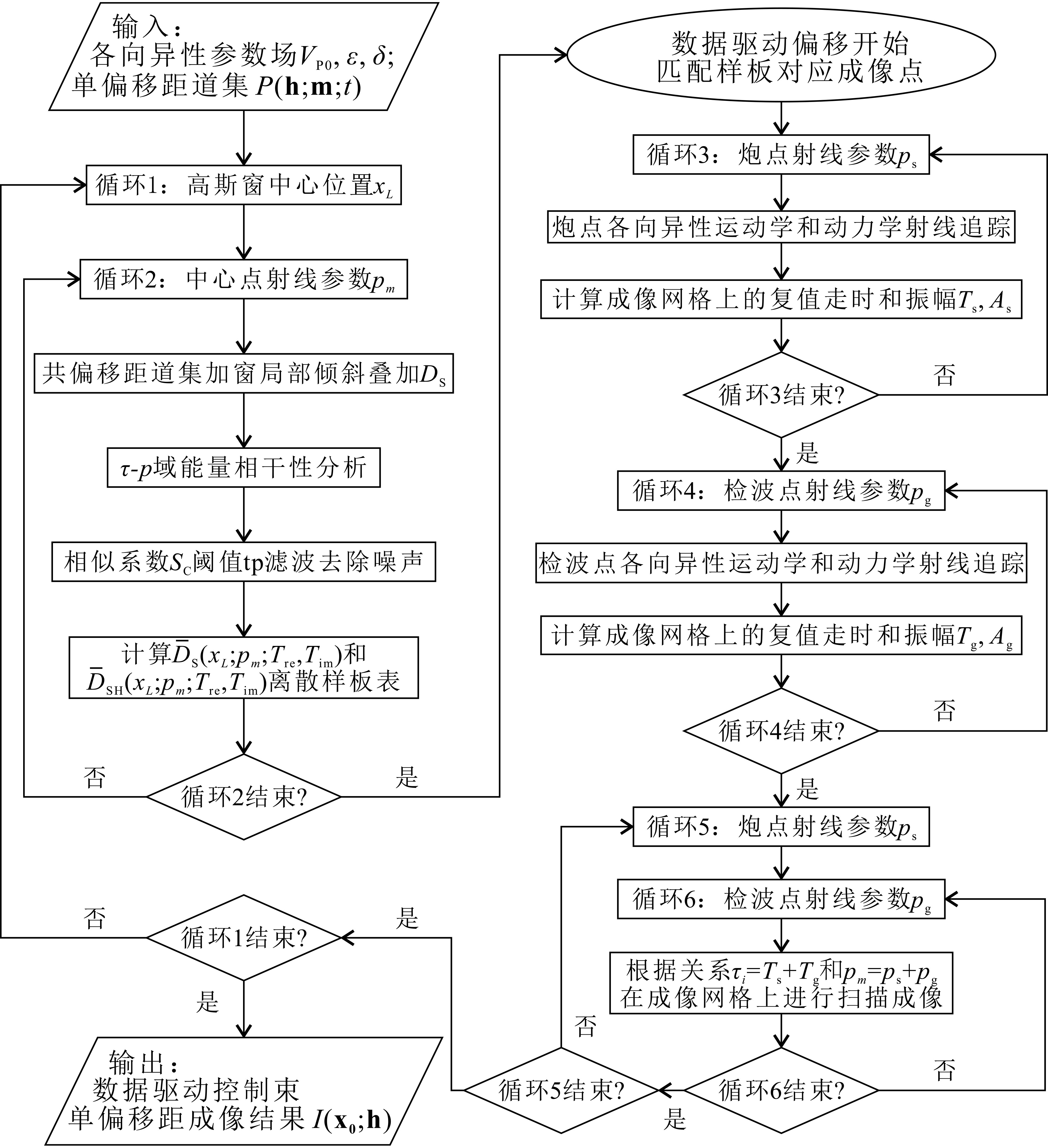
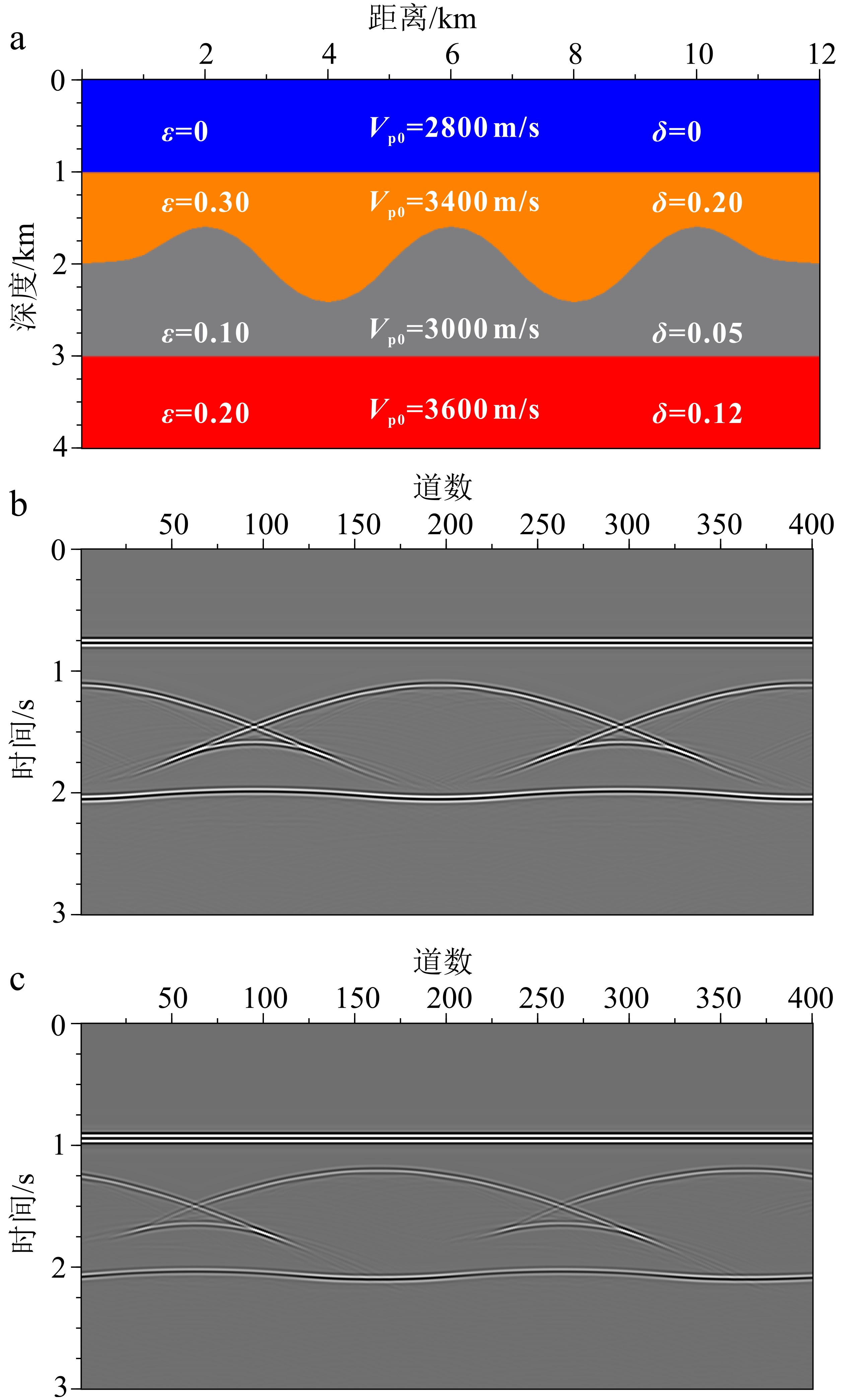
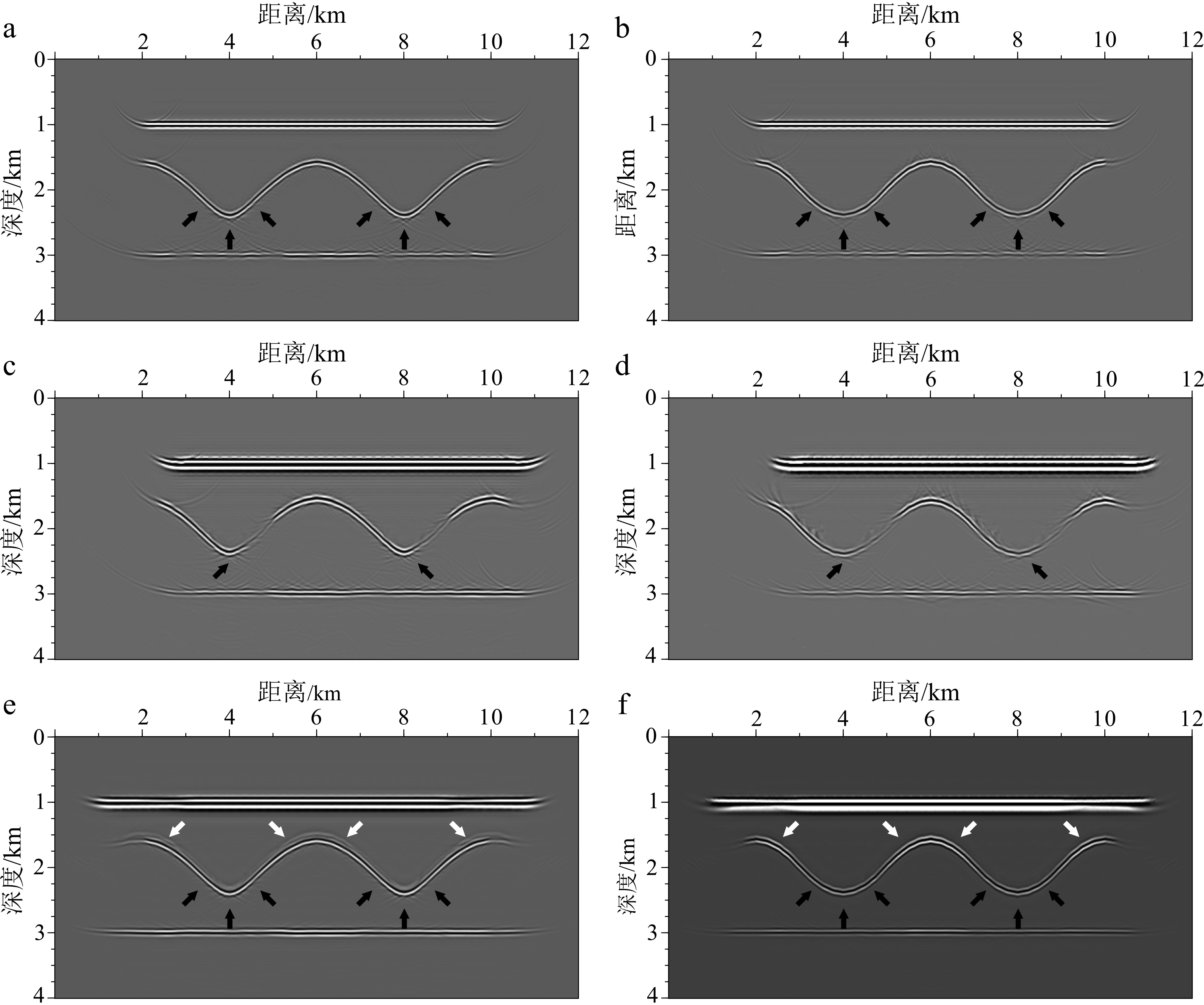
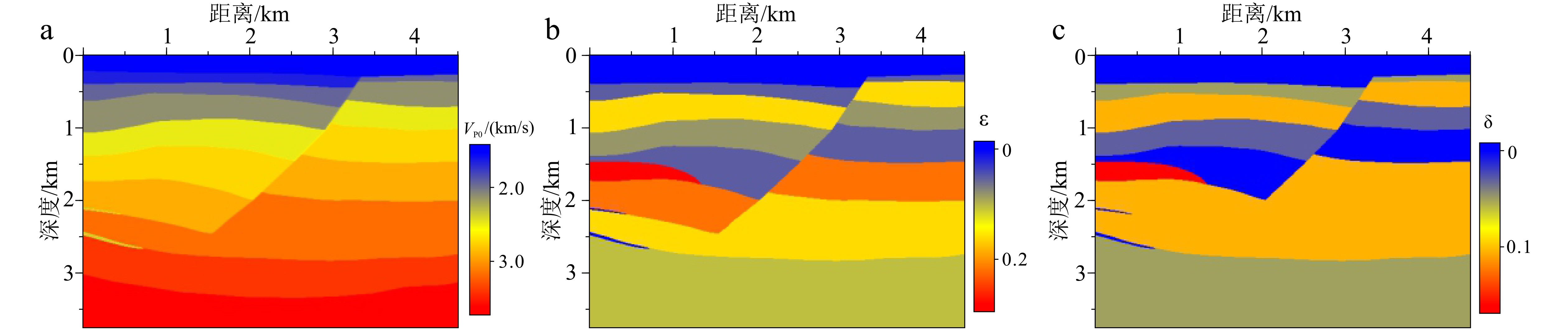
随着勘探区域逐渐从陆地过渡到海洋,勘探目标逐渐趋于复杂化,高精度成像方法已经成为海洋油气勘探的瓶颈技术。高斯束偏移是一种灵活且高效的深度域偏移方法,对实际资料成像具有较好的适应性。该文发展了一种适应于海洋观测系统的高精度高斯束偏移方法,首先将海上接收的共偏移距地震记录进行加窗局部倾斜叠加,通过数学变换将共炮域公式推广到共偏移距域,再从炮点和检波点分别进行射线追踪,最后采用数据驱动的方式进行成像。一方面,考虑到地下介质的各向异性,引入了各向异性射线追踪方程;另一方面,根据有效信号和干扰信号在τ-p域中的相干性差异,在高斯束偏移过程中对地震信号进行控制,降低偏移剖面中的随机噪声,提高同相轴的连续性,最终实现了一种VTI介质共偏移距域数据驱动控制束偏移理论方法。在实现算法的基础上,通过各向异性洼陷模型、修改的SEG/Hess VTI模型及海上实际资料成像试处理,结果表明:各向异性参数对共偏移距道集中的大偏移距信息成像质量改善明显;当地层各向异性不能忽略时,新方法能够更加准确地恢复地下的复杂构造;新方法能够在一定程度上提高低信噪比数据的偏移成像效果。
Abstract:As exploration areas move from the land to the sea, research targets get more complicated, and the high-precision imaging method becomes critical for marine oil and gas exploration. Gaussian beam migration (GBM) is a robust imaging method with high computational efficiency and flexibility. A high-precision GBM method, suitable for marine observation systems, has been developed by the authors in this paper, which contains the transformation between common-shot and common-offset domains and the data-driven framework. On one hand, considering the anisotropy of the subsurface media, an anisotropic ray tracing equation is introduced. On the other hand, based on the semblance difference between signal and disturbance in the τ-p domain, we develop the semblance threshold filtering method to eliminate disturbance during GBM procedure, thereby reducing migration noise. Numerical tests on anisotropic sag model, modified SEG/Hess VTI model and marine data suggest that (1) anisotropic parameters can improve the imaging quality significantly for the large offset data, (2) the proposed method can more accurately recover the complex structure, and (3) the new method may improve the signal-to-noise ratio (S/N) of the migration profile to a certain extent.
-
Key words:
- anisotropy /
- Gaussian beam migration /
- common-offset domain /
- data-driven /
- controlled beam migration
-

-
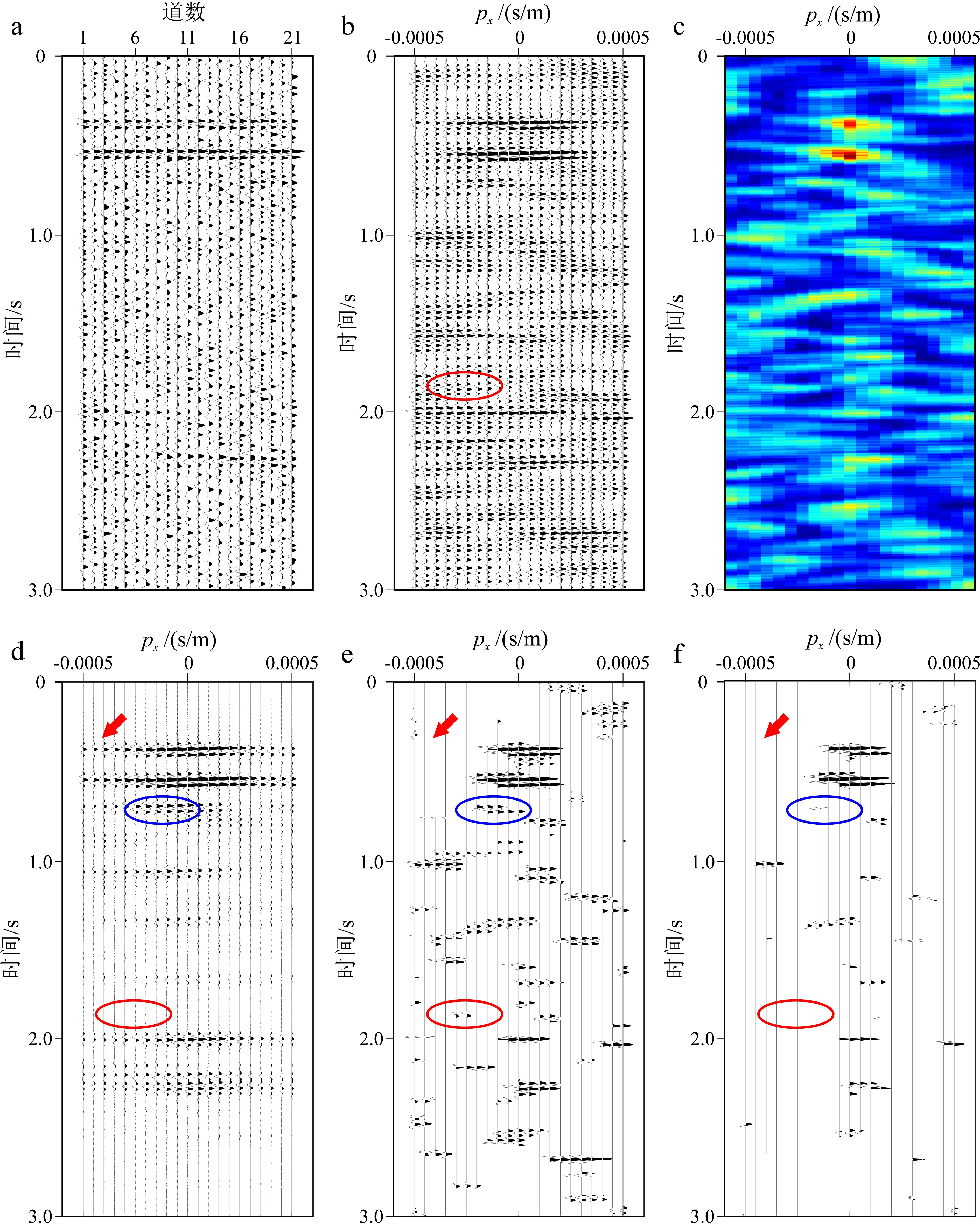
图 8 图7中局部共偏移距道集相干性分析
Figure 8.
-
[1] 吴国忱. 各向异性介质地震波传播与成像[M]. 东营: 中国石油大学出版社, 2006.
WU Guochen. Seismic Wave Propagation and Imaging in Anisotropic Media[M]. Dongying: China University of Petroleum Press, 2006.
[2] Babich V M, Popov M M. Gaussian summation method (review) [J]. Radiophysics and Quantum Electronics, 1989, 32(12): 1063-1081. doi: 10.1007/BF01038632
[3] Popov M M. A new method of computation of wave fields using Gaussian beams [J]. Wave Motion, 1982, 4(1): 85-97. doi: 10.1016/0165-2125(82)90016-6
[4] Popov M M. Ray theory and Gaussian beam method for geophysicists[Z]. EDUFBA, 2002.
[5] Bleistein N. Hagedoorn told us how to do Kirchhoff migration and inversion [J]. The Leading Edge, 1999, 18(8): 918-927. doi: 10.1190/1.1438407
[6] Hill N R. Prestack Gaussian-beam depth migration [J]. Geophysics, 2001, 66(4): 1240-1250. doi: 10.1190/1.1487071
[7] Gray S H, Notfors C, Bleistein N. Imaging using multi-arrivals: Gaussian beams or multi-arrival Kirchhoff?[C]//2002 SEG Annual Meeting. Salt Lake City, Utah: SEG, 2002: 1117-1120.
[8] Liu J, Palacharla G. Multiarrival Kirchhoff beam migration [J]. Geophysics, 2011, 76(5): WB109-WB118. doi: 10.1190/geo2010-0403.1
[9] Kachalov A P, Popov M M. Application of the method of summation of Gaussian beams for calculation of high-frequency wave fields [J]. Soviet Physics Doklady, 1981, 26: 604-606.
[10] Červený V, Popov M M, Pšenčík I. Computation of wave fields in inhomogeneous media-Gaussian beam approach [J]. Geophysical Journal International, 1982, 70(1): 109-128. doi: 10.1111/j.1365-246X.1982.tb06394.x
[11] Červený V. Synthetic body wave seismograms for laterally varying layered structures by the Gaussian beam method [J]. Geophysical Journal International, 1983, 73(2): 389-426. doi: 10.1111/j.1365-246X.1983.tb03322.x
[12] Červený V, Pšenčík I. Gaussian beams in two-dimensional elastic inhomogeneous media [J]. Geophysical Journal International, 1983, 72(2): 417-433. doi: 10.1111/j.1365-246X.1983.tb03793.x
[13] Červený V, Pšenčík I. Gaussian beams in elastic 2-D laterally varying layered structures [J]. Geophysical Journal International, 1984, 78(1): 65-91. doi: 10.1111/j.1365-246X.1984.tb06472.x
[14] Hill N R. Gaussian beam migration [J]. Geophysics, 1990, 55(11): 1416-1428. doi: 10.1190/1.1442788
[15] Alkhalifah T. Gaussian beam depth migration for anisotropic media [J]. Geophysics, 1995, 60(5): 1474-1484. doi: 10.1190/1.1443881
[16] Zhu T F, Gray S H, Wang D L. Prestack Gaussian-beam depth migration in anisotropic media [J]. Geophysics, 2007, 72(3): S133-S138. doi: 10.1190/1.2711423
[17] 段鹏飞, 程玖兵, 陈爱萍, 等. TI介质局部角度域高斯束叠前深度偏移成像[J]. 地球物理学报, 2013, 56(12):4206-4214 doi: 10.6038/cjg20131223
DUAN Pengfei, CHENG Jiubing, CHEN Aiping, et al. Local angle-domain Gaussian beam prestack depth migration in a TI medium [J]. Chinese Journal of Geophysics, 2013, 56(12): 4206-4214. doi: 10.6038/cjg20131223
[18] Protasov M I. 2-D Gaussian beam imaging of multicomponent seismic data in anisotropic media [J]. Geophysical Journal International, 2015, 203(3): 2021-2031. doi: 10.1093/gji/ggv408
[19] 张凯, 段新意, 李振春, 等. 角度域各向异性高斯束逆时偏移[J]. 石油地球物理勘探, 2015, 50(5):912-918
ZHANG Kai, DUAN Xinyi, LI Zhenchun, et al. Angle domain reverse time migration with Gaussian beams in anisotropic media [J]. Oil Geophysical Prospecting, 2015, 50(5): 912-918.
[20] 李振春, 刘强, 韩文功, 等. VTI介质角度域转换波高斯束偏移成像方法研究[J]. 地球物理学报, 2018, 61(4):1471-1481
LI Zhenchun, LIU Qiang, HAN Wengong, et al. Angle domain converted wave Gaussian beam migration in VTI media [J]. Chinese Journal of Geophysics, 2018, 61(4): 1471-1481.
[21] Popov M M, Semtchenok N M, Popov P M, et al. Depth migration by the Gaussian beam summation method [J]. Geophysics, 2010, 75(2): S81-S93. doi: 10.1190/1.3361651
[22] 黄建平, 张晴, 张凯, 等. 格林函数高斯束逆时偏移[J]. 石油地球物理勘探, 2014, 49(1):101-106
HUANG Jianping, ZHANG Qing, ZHANG Kai, et al. Reverse time migration with Gaussian beams based on the Green function [J]. Oil Geophysical Prospecting, 2014, 49(1): 101-106.
[23] Huang J P, Yuan M L, Zhang Q, et al. Reverse time migration with elastodynamic Gaussian beams [J]. Journal of Earth Science, 2017, 28(4): 695-702. doi: 10.1007/s12583-015-0609-9
[24] Gray S H, Bleistein N. True-amplitude Gaussian-beam migration [J]. Geophysics, 2009, 74(2): S11-S23. doi: 10.1190/1.3052116
[25] Protasov M I, Tcheverda V A. True amplitude elastic Gaussian beam imaging of multicomponent walkaway vertical seismic profiling data [J]. Geophysical Prospecting, 2012, 60(6): 1030-1042. doi: 10.1111/j.1365-2478.2012.01068.x
[26] 黄建平, 杨继东, 李振春, 等. 基于有效邻域波场近似的起伏地表保幅高斯束偏移[J]. 地球物理学报, 2016, 59(6):2245-2256 doi: 10.6038/cjg20160627
HUANG Jianping, YANG Jidong, LI Zhenchun, et al. An amplitude-preserved Gaussian beam migration based on wave field approximation in effective vicinity under irregular topographical conditions [J]. Chinese Journal of Geophysics, 2016, 59(6): 2245-2256. doi: 10.6038/cjg20160627
[27] Hu H, Liu Y K, Zheng Y C, et al. Least-squares Gaussian beam migration [J]. Geophysics, 2016, 81(3): S87-S100. doi: 10.1190/geo2015-0328.1
[28] Yuan M L, Huang J P, Liao W Y, et al. Least-squares Gaussian beam migration [J]. Journal of Geophysics and Engineering, 2017, 14(1): 184-196. doi: 10.1088/1742-2140/14/1/184
[29] Yang J D, Zhu H J, McMechan G, et al. Time-domain least-squares migration using the Gaussian beam summation method [J]. Geophysical Journal International, 2018, 214(1): 548-572. doi: 10.1093/gji/ggy142
[30] 黄建平, 袁茂林, 李振春, 等. 双复杂条件下非倾斜叠加精确束偏移方法及应用Ⅰ——声波方程[J]. 地球物理学报, 2015, 58(1):267-276
HUANG Jianping, YUAN Maolin, LI Zhenchun, et al. The accurate beam migration method without slant stack under dual-complexity conditions and its application (I): Acoustic equation [J]. Chinese Journal of Geophysics, 2015, 58(1): 267-276.
[31] 张瑞, 黄建平, 崔超, 等. 莺歌海盆地二维剖面高斯束高精度叠前深度偏移[J]. 海洋地质与第四纪地质, 2017, 37(1):168-175
ZHANG Rui, HUANG Jianping, CUI Chao, et al. High precision Gaussian beam pre-stack depth migration for Yinggehai basin 2D seismic profiles [J]. Marine Geology and Quaternary Geology, 2017, 37(1): 168-175.
[32] Yang J D, Zhu H J. A practical data-driven optimization strategy for Gaussian beam migration [J]. Geophysics, 2018, 83(1): S81-S92. doi: 10.1190/geo2017-0314.1
[33] Vinje V, Roberts G A, Taylor R. Controlled beam migration: a versatile structural imaging tool [J]. First Break, 2008, 26(9): 109-113.
[34] Zhou B, Zhou J, Wang Z L, et al. Anisotropic depth imaging with high fidelity controlled beam migration: A case study in Bohai, offshore China[C]//2011 SEG Annual Meeting. San Antonio, Texas: SEG, 2011: 217-221.
[35] Casasanta L, Gray S, Grion S. Converted-wave controlled beam migration with sparse sources or receivers[C]//75th EAGE Conference & Exhibition. London, UK: EAGE, 2013.
[36] 黄建平, 吴建文, 杨继东, 等. 一种τ-p域二维控制束成像方法[J]. 石油地球物理勘探, 2016, 51(2):342-349
HUANG Jianping, WU Jianwen, YANG Jidong, et al. A 2D control beam migration in the τ-p domain [J]. Oil Geophysical Prospecting, 2016, 51(2): 342-349.
[37] Červený V. Seismic rays and ray intensities in inhomogeneous anisotropic media [J]. Geophysical Journal International, 1972, 29(1): 1-13. doi: 10.1111/j.1365-246X.1972.tb06147.x
[38] Hanyga A. Gaussian beams in anisotropic elastic media [J]. Geophysical Journal International, 1986, 85(3): 473-504. doi: 10.1111/j.1365-246X.1986.tb04528.x
[39] Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations [J]. Geophysics, 2007, 72(1): S49-S58. doi: 10.1190/1.2399371
[40] 高成, 孙建国, 齐鹏, 等. 2D共炮时间域高斯波束偏移[J]. 地球物理学报, 2015, 58(4):1333-1340
GAO Cheng, SUN Jianguo, QI Peng, et al. 2-D Gaussian-beam migration of common-shot records in time domain [J]. Chinese Journal of Geophysics, 2015, 58(4): 1333-1340.
[41] Hale D. Migration by the Kirchhoff, slant stack, and Gaussian beam methods[Z]. Center for Wave Phenomena, Colorado School of Mines, 1992.
[42] 孙夕平, 杜世通. 相干体技术算法研究及其在地震资料解释中的应用[J]. 石油大学学报: 自然科学版, 2003, 27(2):32-35, 40
SUN Xiping, DU Shitong. Development and application of algorithm of coherency cub technique to seismic interpretation [J]. Journal of China University of Petroleum, China: Edition of Natural Science, 2003, 27(2): 32-35, 40.
[43] Bahorich M, Farmer S. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube [J]. The Leading Edge, 1995, 14(10): 1053-1058. doi: 10.1190/1.1437077
[44] Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attributes using a semblance-based coherency algorithm [J]. Geophysics, 1998, 63(4): 1150-1165. doi: 10.1190/1.1444415
[45] Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherency calculations in the presence of structural dip [J]. Geophysics, 1999, 64(1): 104-111. doi: 10.1190/1.1444508
[46] Neidell N S, Taner M T. Semblance and other coherency measures for multichannel data [J]. Geophysics, 1971, 36(3): 482-497. doi: 10.1190/1.1440186
-




 下载:
下载: