基于指标信度测度赋权的岩溶隧道水害危险性集对云评价研究

蒋英礼; 崔杰; 王景梅; 张彦龙

doi:10.11932/karst20220208

基于指标信度测度赋权的岩溶隧道水害危险性集对云评价研究

1.
广东交通职业技术学院，广东广州 510650

2.
广州大学，广东广州 510006

3.
广东华路交通科技有限公司，广东广州 510420

基金项目: 国家自然科学基金资助项目（51578167）；广东省普通高校特色创新项目（2021KTSCX221）；广州市基础研究计划基础与应用基础研究项目（2022-1720）

详细信息

作者简介: 蒋英礼（1984－），男，副教授，博士研究生，从事隧道工程方面的教学与研究工作。E-mail：jiangyingl@163.com

通讯作者: 崔杰（1962－），男，博士，博士生导师，研究员，从事岩土工程方面的教学与研究工作。E-mail：jcui2009@hotmail.com

中图分类号: U457.2

收稿日期: 2021-04-05

刊出日期: 2022-04-25

Risk assessment of tunnel flood based on the weighting of index reliability measurement and set pair cloud

1.
Guangdong Communication Polytechnic, Guangzhou, Guangdong 510650, China

2.
Guangzhou University, Guangzhou, Guangdong 510006, China

3.
Guangdong Hualu Transport Technology Co., Ltd., Guangzhou, Guangdong 510420, China

More Information

Corresponding author: CUI Jie, jcui2009@hotmail.com

Received Date: 05 April 2021

Publish Date: 25 April 2022

摘要

摘要:
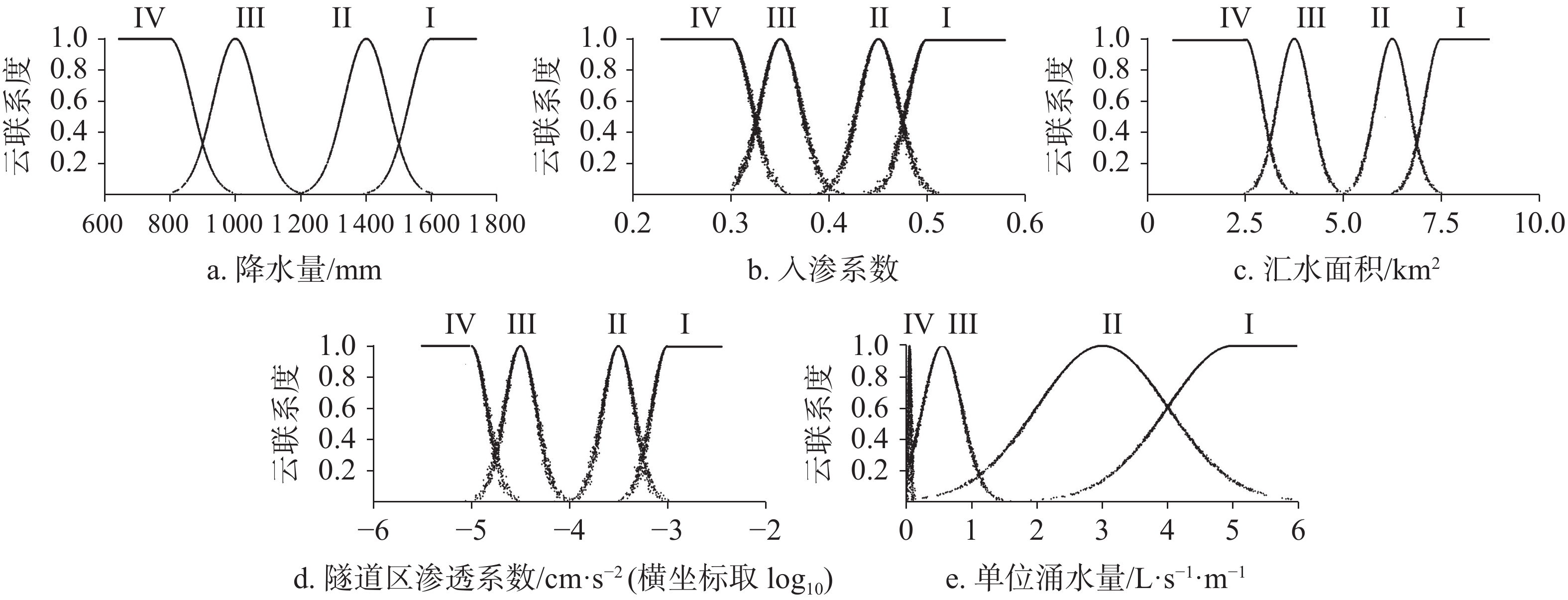
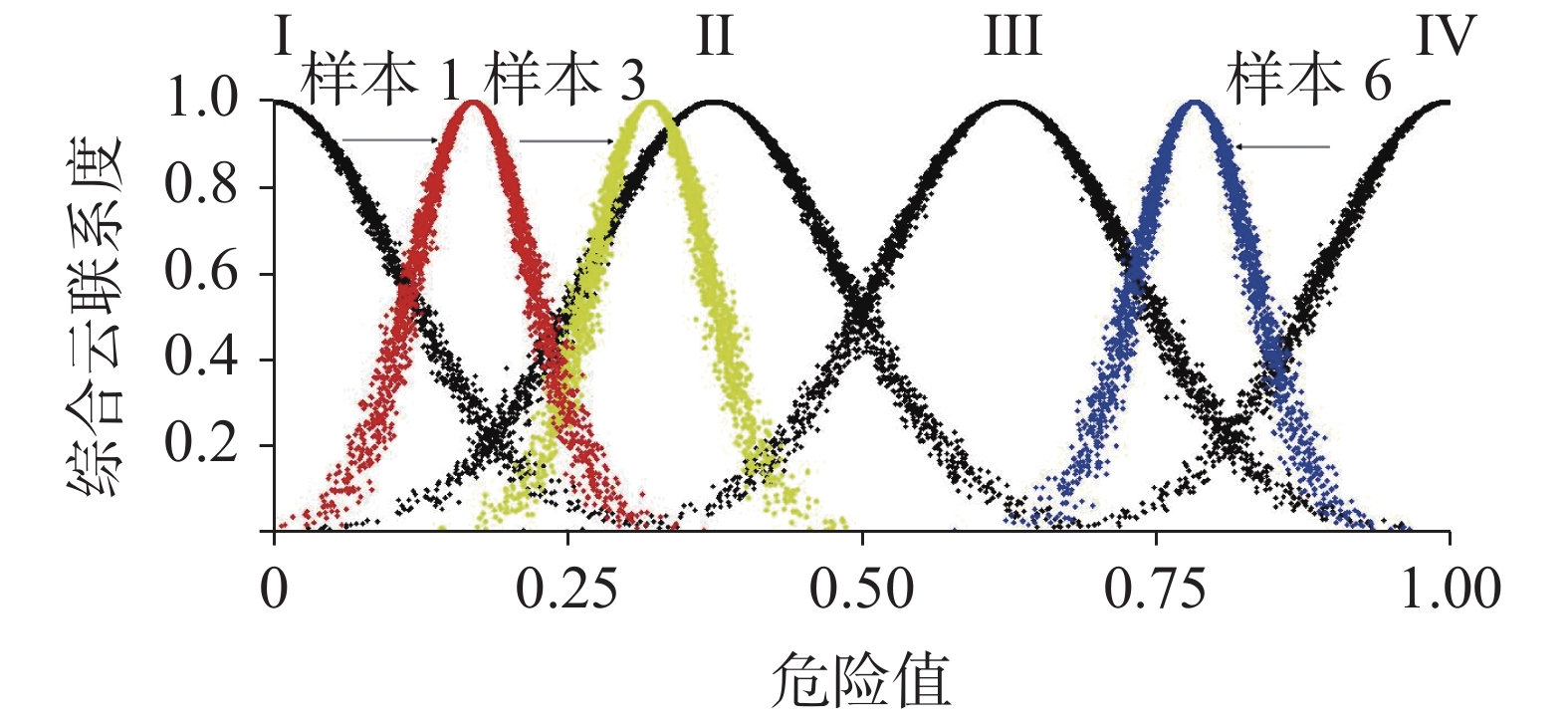
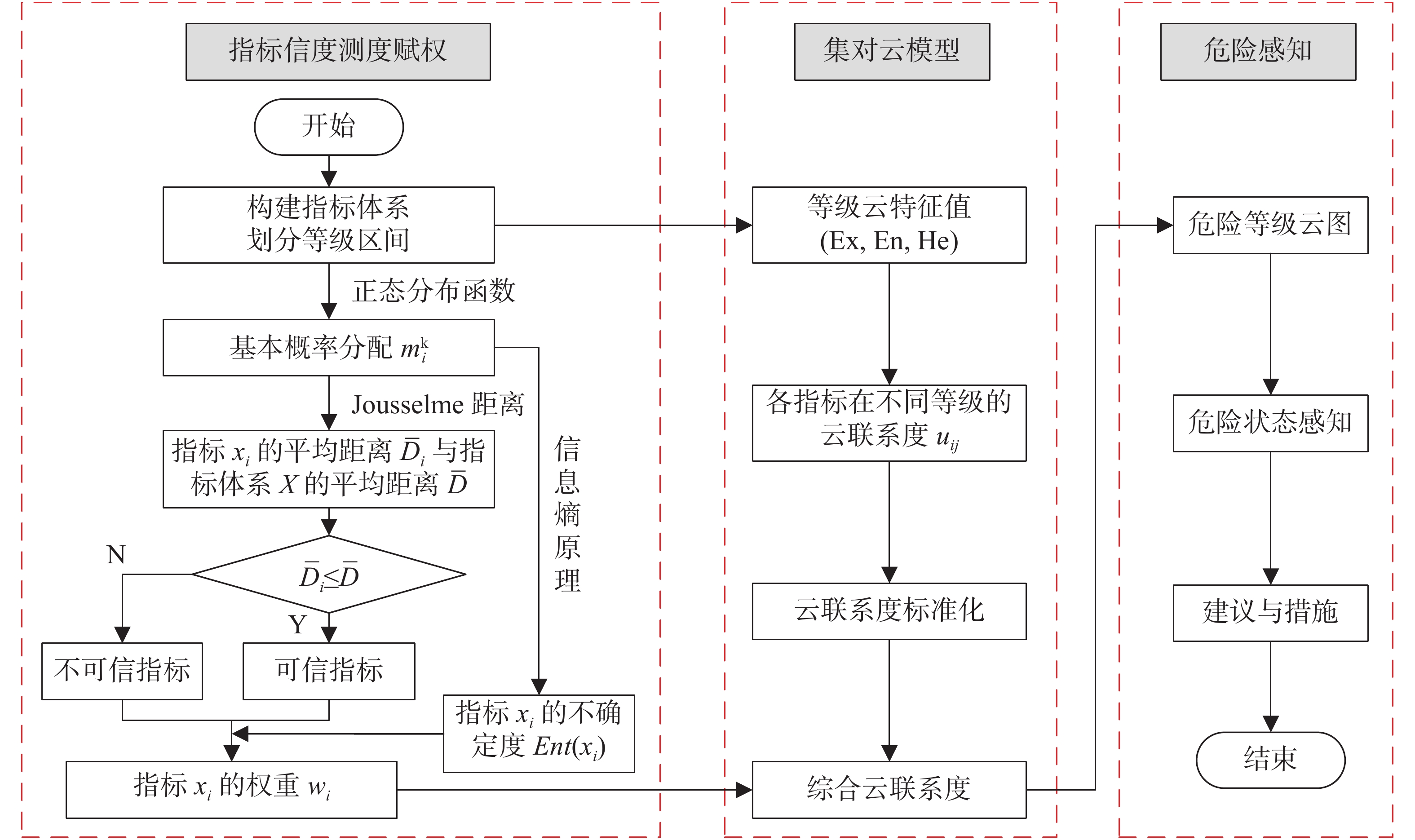
隧道水害危险性评价是一个非线性复杂的不确定系统问题。首先，针对其评价指标参数具有不确定性、模糊性和随机性等特点，在充分考虑岩溶隧道水害危险性评价指标关联性的基础上，提出了基于Jousselme距离的指标信度测度动态赋权理论，实现不同的实例、不同的指标实测值对整个系统的动态赋权，降低实际工作中由于指标实测值误差或错误导致评价结果偏差的风险；其次，运用云理论优化集对联系度，与所得权重加权得出系统综合云联系度，并与等级评价区间期望加权平均得到危险值，同时生成对应的等级云图判定隧道水害危险性等级，进而判定岩溶隧道水害危险状态，实现水害危险等级判定的可视化；再次，基于大气降水为岩溶隧道水害主要来源的视角，选取年均降水量、入渗系数、汇水面积、渗透系数和单位涌水量5项指标作为集对云评价指标，并以6条典型岩溶隧道为样本数据进行模型检验，发现评价结果与其他方法的评价结果相吻合，证明了该模型的可靠性和有效性。最后，将模型应用于京珠高速公路媲双坳岩溶隧道水害事故中，评价结果与实际情况相符，采取与评价等级相对应的处治措施，取得了良好的水害治理效果，表明该模型具有工程实用价值，评价流程可操作性强，为岩溶隧道水害的预测和防治提供参考。
- 指标信度测度 /
- 隧道水害 /
- 危险性评价 /
- 集对云
Abstract:
Tunnel flood assessment is a nonlinear and complex system with uncertainty. Scientific and reasonable flood grading evaluation and corresponding prevention and treatment measures have become the primary problem to be solved in the construction and operation of karst tunnels. Firstly, aimed at the uncertainty, fuzziness and randomness of evaluation index parameters, the correlation between indexes by the multi-evidence correlation coefficient of Jousselme distance are analyzed in this study. The dynamic weighting theory of index reliability measurement based on Jousselme distance is also put forward. With the weighting method, the accurate weight of each index can be obtained according to the reliability classification of indexes. Thus, the dynamic weighting of the whole system by the measured values of different cases and indexes is realized, and the risk of deviation of evaluation results caused by the error or error of measured values of indexes in practice is reduced; thus, the robustness of the evaluation model will be enhanced.Secondly, based on the theory and idea of uncertain artificial intelligence, and with the combination of the eigenvalues in cloud theory and the set pair theory, the cloud theory to optimize the set pair connection degree is used to obtain risk assessment indexes of karst tunnel flood. The index cloud connection degree and index reliability measurement are weighted by the dynamic weighting method to obtain the degree of system comprehensive cloud connection, and the risk value is obtained by the expected weighted average of the grading evaluation interval. At the same time, the corresponding grade cloud map is generated to determine the flood grade of karst tunnel. Accordingly, the flood state of karst tunnel is determined, and the visualization of flood grade determination is realized.Thirdly, the karst tunnel flood occurs in a complex system composed of both the tunnel and the external environment; therefore, its risk assessment is affected by many factors, and the evaluation index system should be established in a comprehensive and concise way. From the perspective that atmospheric precipitation is the main source of flood in karst tunnel, five correlation indexes-annual precipitation, infiltration coefficient, catchment area, permeability coefficient and unit water inflow-are constructed as evaluation indexes of set pair cloud of karst tunnel flood in this study. On this basis, the grading standard of each evaluation index and its corresponding cloud map of flood grade are established. In order to verify the accuracy and effectiveness of the set pair cloud model and its evaluation index system constructed based on the weighting of the index reliability measurement, the data of six typical karst tunnel samples for the model test is collected. Consistency between evaluation results and those of other methods proves the reliability and effectiveness of the model proposed in this study. Finally, this model has been applied to the flood accident of Pishuangao karst tunnel of Beijing-Zhuhai expressway, the results of which are also consistent with the actual situation of the project. At the same time, the treatment measures corresponding to Grade I have achieved effective flood control. The result shows that the set pair cloud model constructed in this study based on the weighting of the index reliability measurement takes into account the correlation between the evaluation indexes, the uncertainty of the evaluation system and the ambiguity of the evaluation index grade. The model can improve the accuracy of flood risk assessment in karst tunnels, and the evaluation process of this model is highly maneuverable. In fact, this model can provide a new method for rapid and effective analysis of flood in karst tunnels, and can also provide reference and guidance for the prediction and prevention of flood in karst tunnels in China.
- index reliability measurement /
- tunnel flood /
- risk assessment /
- set pair cloud (SPC)

HTML全文

图 1 岩溶隧道水害危险性评价集对云模型结构图及评价流程

Figure 1.

下载: 全尺寸图片幻灯片

图 2 隧道水害危险性评价指标的集对云模型

Figure 2.

下载: 全尺寸图片幻灯片

图 3 样本1、样本3和样本6综合云与评价标准云对比图

Figure 3.

下载: 全尺寸图片幻灯片

图 4 媲双坳隧道水害事故图

Figure 4.

下载: 全尺寸图片幻灯片

图 5 地震映像法探测结果平面展开图

Figure 5.

下载: 全尺寸图片幻灯片

表 1 水害危险性等级表述及相应处治措施

Table 1. Risk grades of tunnel flood and its corresponding treatment

评价结果	危险值U
评价结果	[0，0.25)	[0.25，0.5)	[0.5，0.75)	[0.75，1.0]
云模型SPC	(0，0.107，0.01)	(0.375，0.107，0.01)	(0.625，0.107，0.01)	(1，0.107，0.01)
危险性等级	危险性极大（Ⅰ）	危险性较大（Ⅱ）	危险性一般（Ⅲ）	危险性小（Ⅳ）
危险性描述	隧道出现衬砌结构破损、涌水涌泥事故，严重影响隧道安全及行车安全，急需加固处治	隧道出现严重渗漏水，影响隧道安全及行车安全，需要加固处治	隧道出现一般渗漏水	隧道几乎无渗漏水或渗漏水很少
加固处治措施	进行隧道专项检测，掌握隧道结构安全状态，采取封缝、衬砌背后注浆及岩洞回填封堵、植筋加固、地表注浆，并配以地表封堵引排与洞内引排等多种措施	进行隧道专项检测，保证隧道结构安全，并配以封缝、衬砌背后回填封堵及注浆、植筋加固等工程措施	需重点部位加强监控检测，并配以封缝等处治措施	无需加固，日常维护检修

下载: 导出CSV

表 2 隧道水害危险性评价指标分级表

Table 2. Index grades of risk assessment for tunnel flood

评价指标	评价等级
评价指标	危险性极大（Ⅰ）	危险性较大（Ⅱ）	危险性一般（Ⅲ）	危险性小（Ⅳ）
年均降水量x₁/mm	>1 600	1 200～1 600	800～1 200	<800
入渗系数x₂	>0.5	0.4～0.5	0.3～0.4	<0.3
汇水面积x₃/km²	>7.5	5～7.5	2.5～5	<2.5
渗透系数x₄/cm·s⁻¹	>10⁻³	10⁻⁴～10⁻³	10⁻⁵～10⁻⁴	<10⁻⁵
单位涌水量x₅/L·s⁻¹·m⁻¹	>5	1～5	0.1～1	<0.1

下载: 导出CSV

表 3 岩溶隧道样本及相应指标的测定值

Table 3. Measured values of sample indexes

样本编号	岩溶隧道名称	评价指标
样本编号	岩溶隧道名称	年均降雨量x₁/mm	入渗系数x₂	汇水面积x₃/km²	渗透系数x₄/cm·s⁻¹	单位涌水量x₅/L·s⁻¹·m⁻¹
1	岭头隧道	2 450	0.44	2.93	3×10⁻³	4.73
2	葡萄山隧道	2 200	0.43	3.57	7×10⁻²	4.39
3	马鹿箐隧道	892	0.51	4.89	4×10⁻⁴	4.53
4	竹林坪隧道	1 345	0.42	2.98	5×10⁻⁴	3.37
5	双峰隧道	956	0.32	1.57	2×10⁻⁶	0.70
6	太行山隧道	624	0.25	2.95	8×10⁻⁷	0.12

下载: 导出CSV

表 4 隧道样本各评价指标权值

Table 4. Weight coefficients of indexes of sample tunnels

样本编号	评价指标
样本编号	x₁	x₂	x₃	x₄	x₅
1	0.184	0.165	0.102	0.292	0.256
2	0. 361	0.097	0.160	0.179	0.203
3	0.115	0.248	0.244	0.144	0.249
4	0.271	0.214	0.073	0.153	0.289
5	0.274	0.297	0.082	0.154	0.193
6	0.242	0.276	0.090	0.310	0.082

下载: 导出CSV

表 5 各样本隧道的指标云联系度、综合云联系度和评价结果

Table 5. Index cloud connection degree, comprehensive connection degree and evaluation results of sample tunnels

样本编号	指标云联系度	综合云联系度	危险值U	评价结果			是否发生过水害
样本编号	指标云联系度	综合云联系度	危险值U	本文	文献[11]	文献[12]	是否发生过水害
1	μ₁₁=1+0i₁+0i₂+0j μ₁₂=0.256+0.665i₁+0.076i₂+0.003j μ₁₃=0+0.005i₁+0.445i₂+0.550j μ₁₄=1+0i₁+0i₂+0j μ₁₅=0.623+0377i₁+0i₂+0j	μ₁=0.678+0.207i₁+0.058i₂+0.057j	0.170	I	I	I	是
2	μ₂₁=0.992+0.008i₁+0i₂+0j μ₂₂=0.004+0.075i₁+0.665i₂+0.256j μ₂₃=0+0.027i₁+0.602i₂+0.371j μ₂₄=1+0i₁+0i₂+0j μ₂₅=0.572+0.428i₁+0i₂+0j	μ₂=0.653+0.102i₁+0.161i₂+0.084j	0.223	I	I	I	是
3	μ₃₁=0 +0.007i₁+0.483i₂+0.510j μ₃₂=0.721+0.278i₁+0.001i₂+0j μ₃₃=0.045+0.389i₁+0.494i₂+0.072j μ₃₄=0.516+0.484i₁+0i₂+0j μ₃₅=0.593+0.407i₁+0i₂+0j	μ₃=0.423+0.335i₁+0.170i₂+0.072j	0.324	Ⅱ	Ⅱ	Ⅱ	是
4	μ₄₁=0.420+0.497i₁+0.064i₂+0.019j μ₄₂=0.141+0.631i₁+0.212i₂+0.016j μ₄₃=0+0.006i₁+0.458i₂+0.536j μ₄₄=0.500+0.500i₁+0i₂+0j μ₄₅=0.434+0.566i₁+0i₂+0j	μ₃=0.346+0.510i₁+0.096i₂+0.048j	0.328	Ⅱ	Ⅱ	Ⅱ	是
5	μ₅₁=0 +0.021i₁+0.582i₂+0.397j μ₅₂=0+0.006i₁+0.463i₂+0.531j μ₅₃=0+0 i₁+0.155i₂+0.845j μ₅₄=0.258+0.190i₁+0.203i₂+0.349j μ₅₅=0.091+0.277i₁+0.632i₂+0j	μ₅=0.057+0.091i₁+0.463i₂+0.389j	0.713	Ⅲ	Ⅲ	Ⅲ	否
6	μ₆₁=0.048+0i₁+0.107i₂+0.845j μ₆₂=0+0i₁+0.115i₂+0.885j μ₆₃=0+0.005i₁+0.450i₂+0.545j μ₆₄=0.731+0.269i₁+0i₂+0j μ₆₅=0.043+0.139i₁+0.306i₂+0.512j	μ₆=0.242+0.094i₁+0.124i₂+0.540j	0.797	Ⅳ	Ⅳ	Ⅳ	否

下载: 导出CSV

参考文献(17)

[1]	田四明, 王伟, 巩江峰. 中国铁路隧道发展与展望(含截至2020年底中国铁路隧道统计数据)[J]. 隧道建设(中英文), 2021, 41(2): 308-325. TIAN Siming, WANG Wei, GONG Jiangfeng. Development and prospect of railway tunnels in China (including statistics of railway tunnels in China by the end of 2020)[J]. Tunnel Construction, 2021, 41(2): 308-325.
[2]	蒋树屏. 中国公路隧道数据统计[J]. 隧道建设(中英文), 2017, 37(5): 643-644. JIANG Shuping. Statistics of highway tunnels in China[J]. Tunnel Construction, 2017, 37(5): 643-644.
[3]	陈建芹, 冯晓燕, 魏怀, 冯欢欢. 中国水下隧道数据统计[J]. 隧道建设(中英文), 2021, 41(3): 483-516. CHEN Jianjin, Feng Xiaoyan, WEI Huai, FENG Huanhuan. Statistics of underwater tunnels in China[J]. Tunnel Construction, 2021, 41(3): 483-516.
[4]	潘海泽, 黄涛, 杨海静, 唐仙. 运营隧道渗漏水灾害分类和等级评定方法[J]. 干旱区地理, 2009, 32(1): 145-151. PAN Haize, HUANG Tao, YANG Haijing, TANG Xian. Classification and grading assessment method of leakage disasters in running tunnel[J]. Arid Land Geography, 2009, 32(1): 145-151.
[5]	张彦龙, 田卿燕, 张建同. 广东地区某公路岩溶隧道水害分析及其数值模拟研究[J]. 中国岩溶, 2018, 37(2): 307-313. ZHANG Yanlong, TIAN Qingyan, ZHANG Jiantong. Water disaster analysis and numerical simulation of a karst tunnel in a highway of Guangdong Province[J]. Carsologica Sinica, 2018, 37(2): 307-313.
[6]	蒋英礼, 张彦龙, 王景梅. 基于未确知测度- SPA 的岩溶隧道水害危险性评价[J] . 人民长江, 2021, 52(5): 78-85. JIANG Yingli, ZHANG Yanlong, WANG Jingmei. Risk assessment of Karst tunnels flood based on multilevel uncertainty measurement-set pair analysis theory[J]. Yangtze River, 2021, 52(5): 78-85.
[7]	刘敏捷, 伍毅敏, 高劲松. 公路隧道隧底结构水害机理研究[J]. 地下空间与工程学报, 2017, 13 (1) : 319-326. LIU Minjie, WU Yimin, GAO Jinsong. Research on the Water Damage Mechanism of the Bottom Structure of Highway Tunnel[J]. Chinese Journal of Underground Space and Engineering, 2017, 13 (1) : 319-326.
[8]	刘浩, 祝志恒, 李林毅. 京珠高速公路洋碰隧道水害原因分析及安全性评价[J]. 隧道建设(中英文), 2020, 40(5): 747-754. LIU Hao, ZHU Zhiheng, LI Linyi. Causes analysis of water disease in Yangpeng tunnel on Beijing-Zhuhai expressway and its safety evaluation. Tunnel Construction, 2020, 40(5): 747-754.
[9]	中华人民共和国水利部. 水工隧洞设计规范[S]. 北京: 中国水利水电出版社, 2016. Ministry of water resources of the People's Republic of China. Design specifications for hydraulic tunnels[S]. Beijing: China Water Resources and Hydropower Press, 2016.
[10]	谭洪强, 邓红卫, 王杰, 侯志勇, 胡道礼. 公路隧道水害倾向性分级的Bayes判别法及应用[J]. 中国安全生产科学技术, 2015(6): 122-127. TAN Hongqiang, DENG Hongwei, WANG Jie, HOU Zhiyong, HU Daoli. Bayes discriminant analysis on flood tendency classification of highway tunnel and its application[J]. Journal of Safety Science and Technology, 2015(6): 122-127.
[11]	游波, 施式亮, 刘何清, 李润求, 罗文柯. 基于信息熵和集对分析理论的公路隧道水害倾向性判定[J]. 公路交通科技, 2019(6): 73-78. YOU Bo, SHI Shiliang, LIU Heqing, LI Runqiu, LUO Wenke. Determination of flood tendency of highway tunnel based on entropy and set pair analysis theory[J]. Journal of Highway and Transportation Research and Development, 2019(6): 73-78.
[12]	谭洪强, 邓红卫, 马浩鹏, 袁晓, 刘冰玉. 基于未确知测度理论的公路隧道水害危险性评价[J]. 中国安全生产科学技术, 2015, 11(4): 166-172. TAN Hongqiang, DENG Hongwei, MA Haopeng, YUAN Xiao, LIU Bingyu. Risk assessment on highway tunnel flood based on uncertainty measurement theory[J]. Journal of Safety Science and Technology, 2015,11(4): 166-172.
[13]	李德毅, 杜鹢. 不确定性人工智能(第2版)[M]. 北京: 国防工业出版社, 2014 LI Deyi, DU Yu. Uncertain Artificial Intelligence (2^nd Edition) [M]. Beijing: National Defense Industry Press, 2014.
[14]	苏永华, 何满潮, 孙晓明. 岩体模糊分类中隶属函数的等效性[J]. 北京科技大学学报, 2007, 29(7): 670-675 SU Yonghua, HE Manchao, SUN Xiaoming. Equivalent characteristic of membership function type in rock mass fuzzy classification[J]. Journal of University of Science and Technology Beijing, 2007, 29(7): 670-675.
[15]	Jousselme A L, Dominic G, Eloi B. A new distance between two bodies of evidence[J]. Information Fusion, 2001(2):91-101.
[16]	赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000. ZHAO Keqin. Set pair analysis and its preliminary application [M]. Hangzhou: Zhejiang Science and Technology Press, 2000.
[17]	戴建玲, 雷明堂. 公路工程岩溶环境一、二级区划[J]. 中国岩溶, 2013, 32(2): 153-160,174. DAI Jianling, LEI Mingtang. First and second level karst environment zoning for highway engineering[J]. Carsologica Sinica, 2013, 32(2): 153-160, 174.