Experimental Study of the Strength Distribution of Irregular Copper−molybdenum Ore Particles
-
摘要:
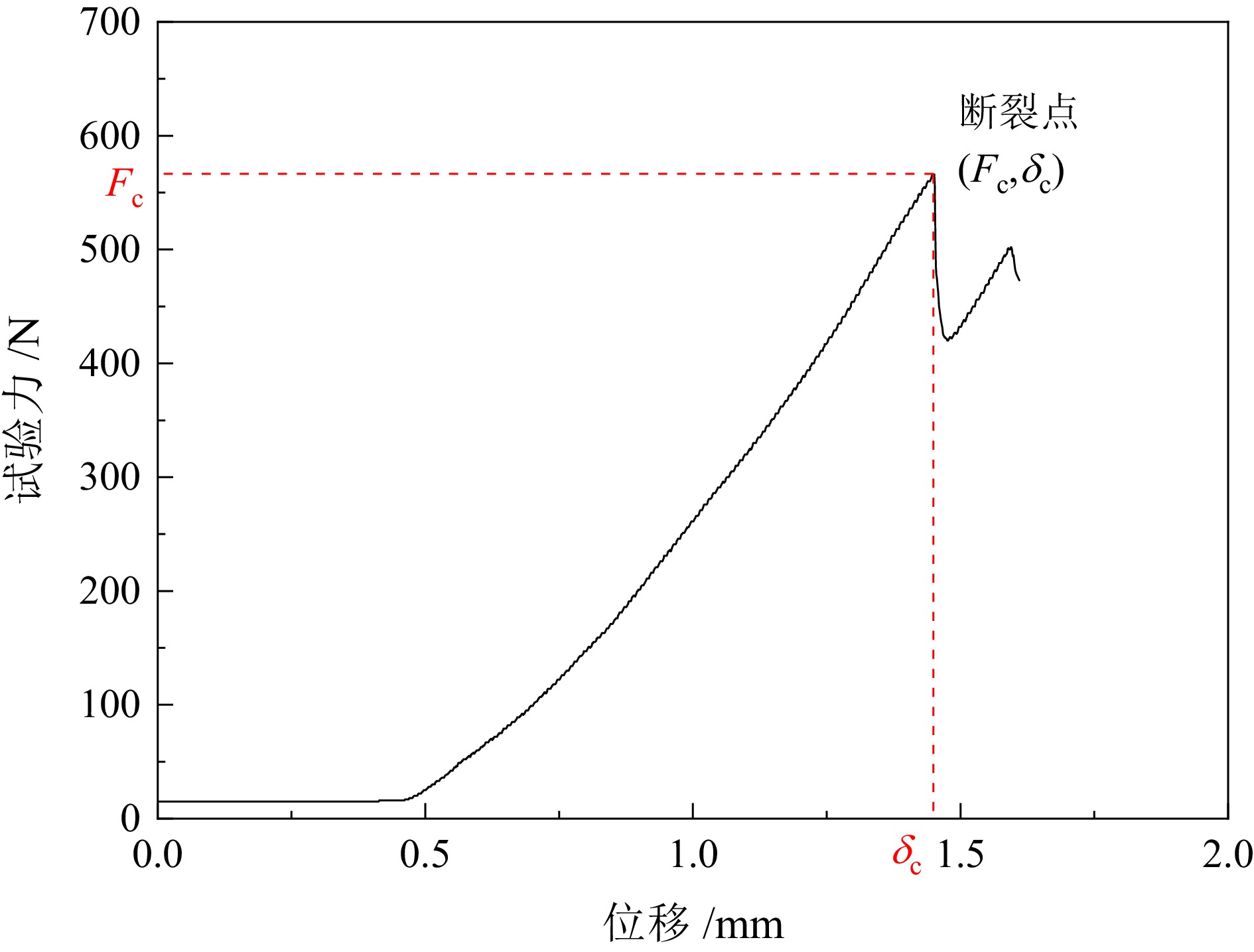
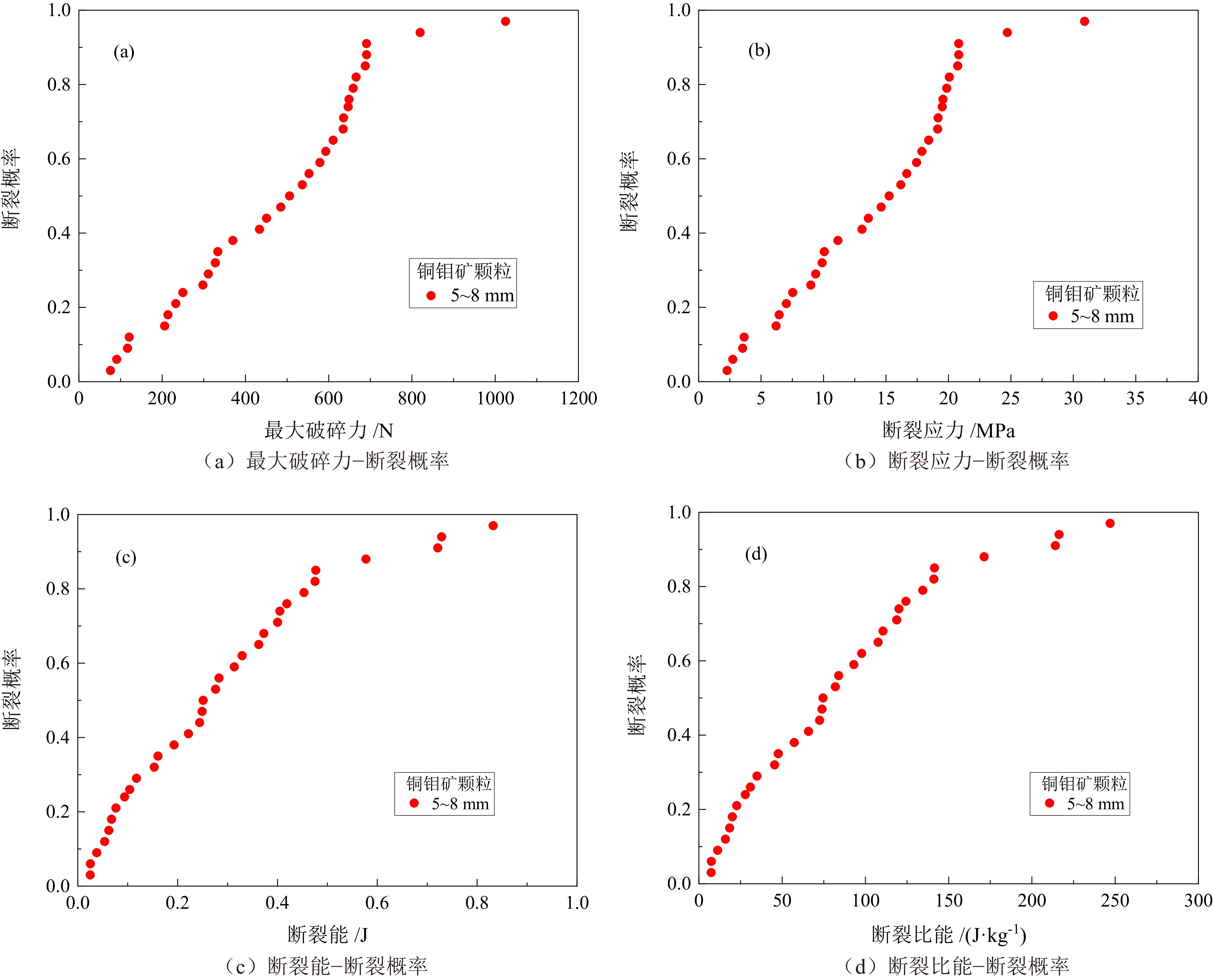
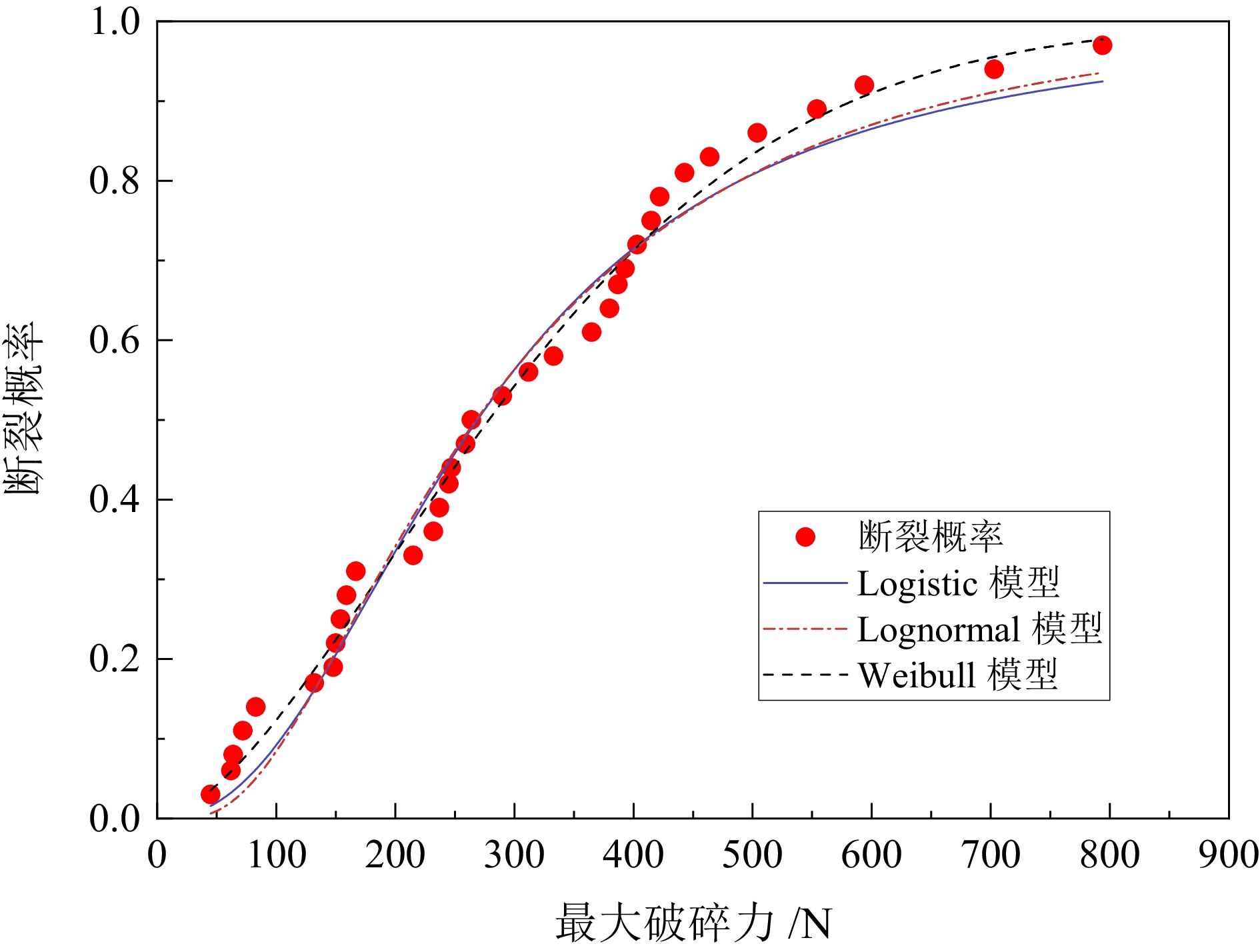
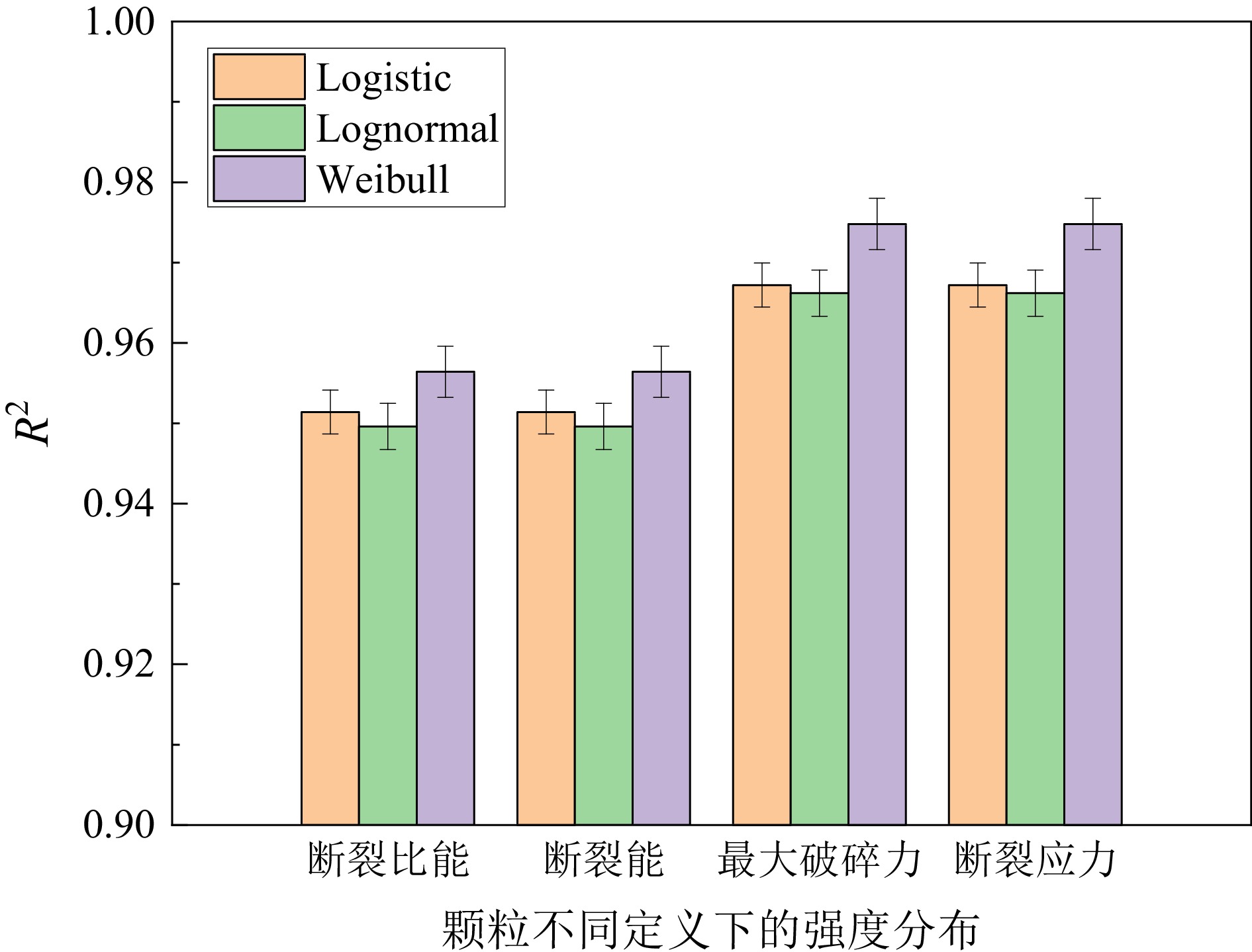
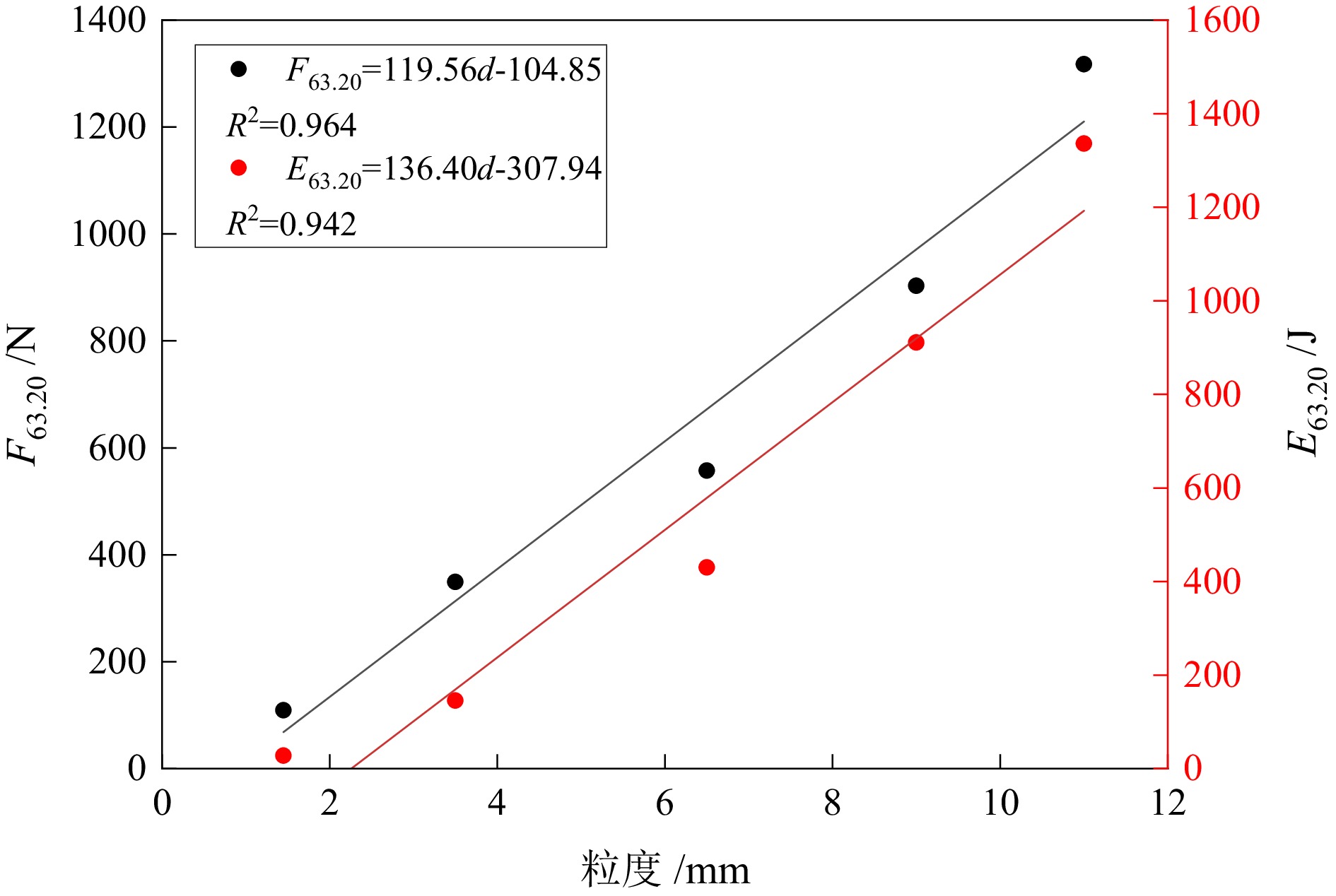
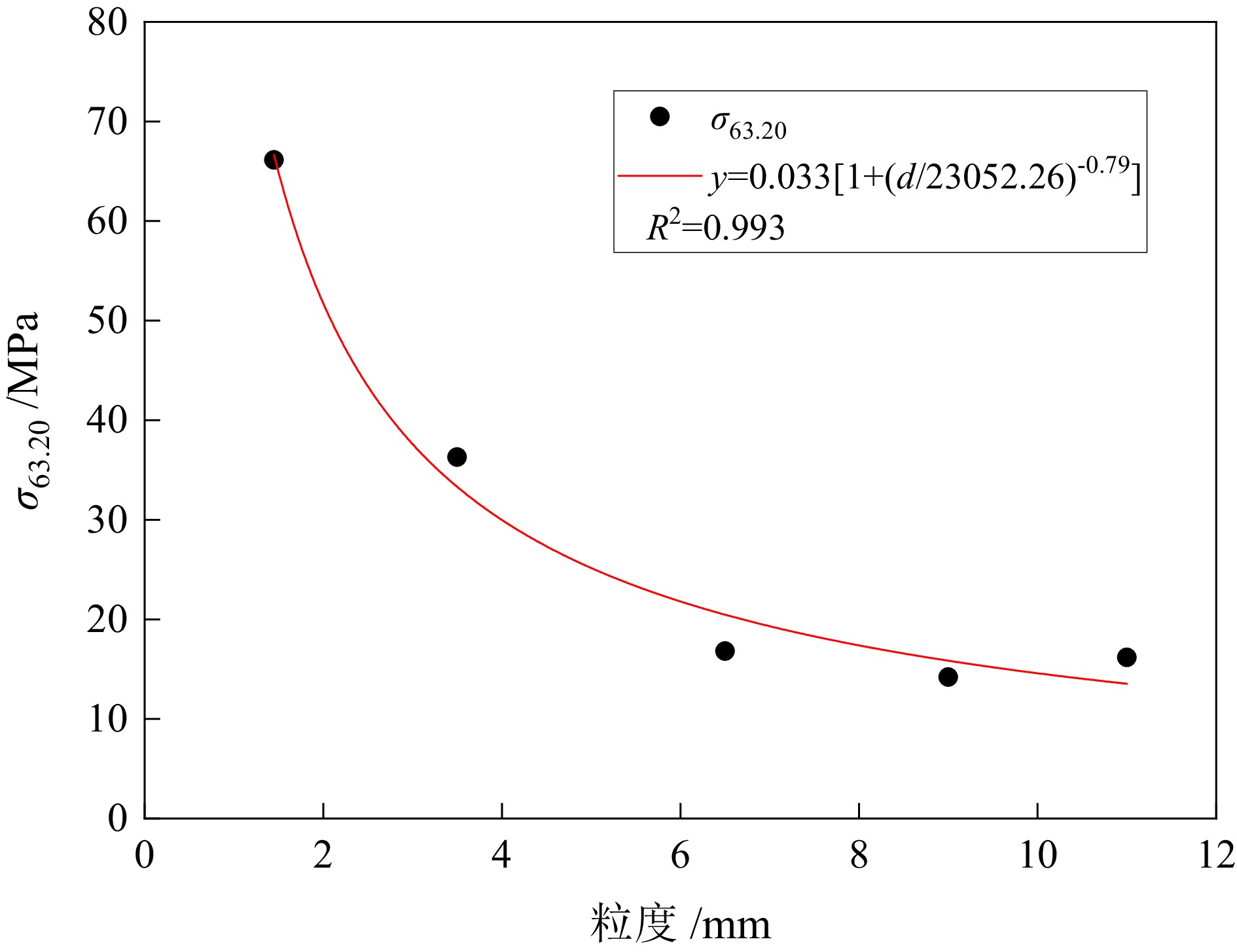
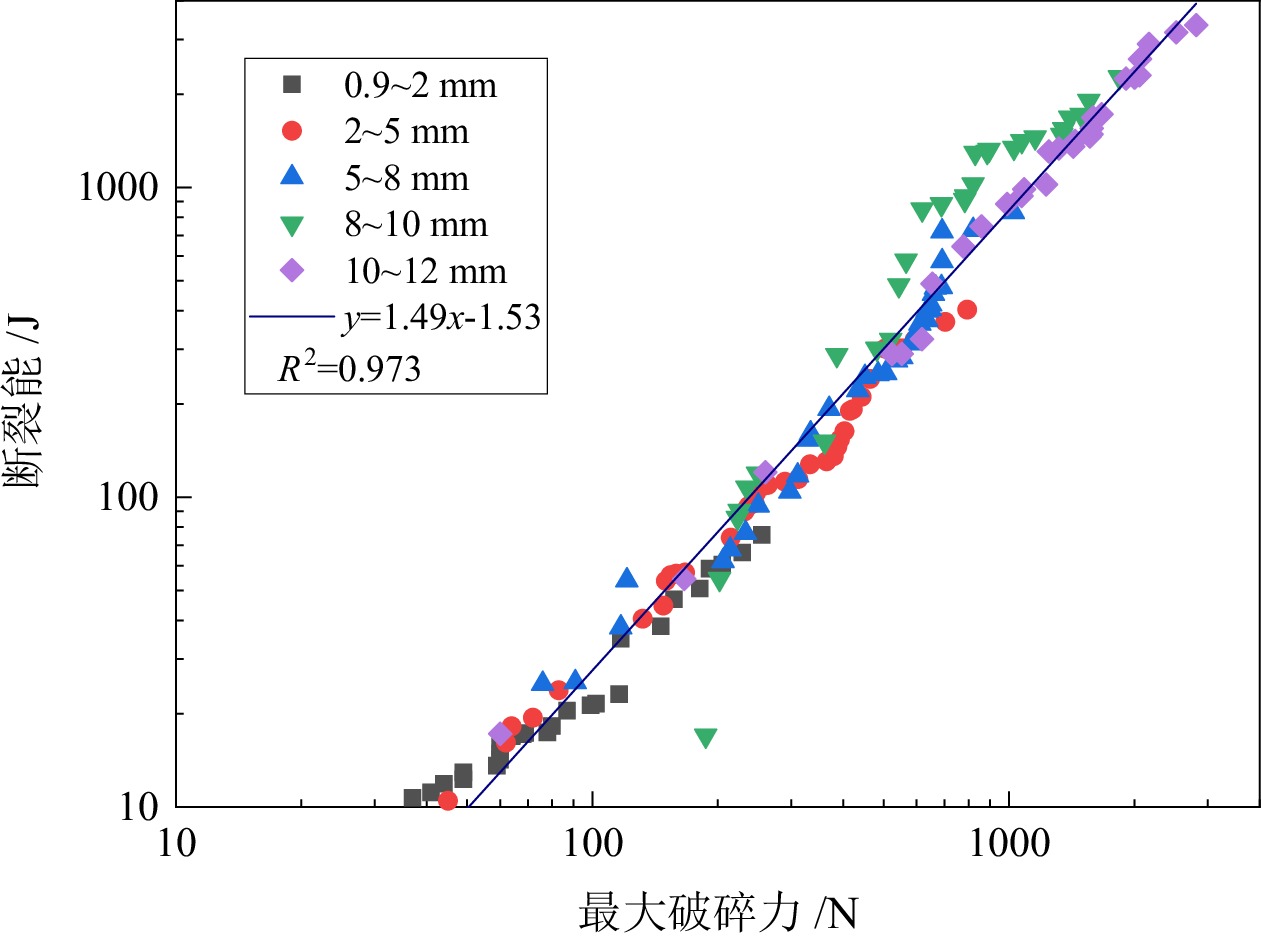
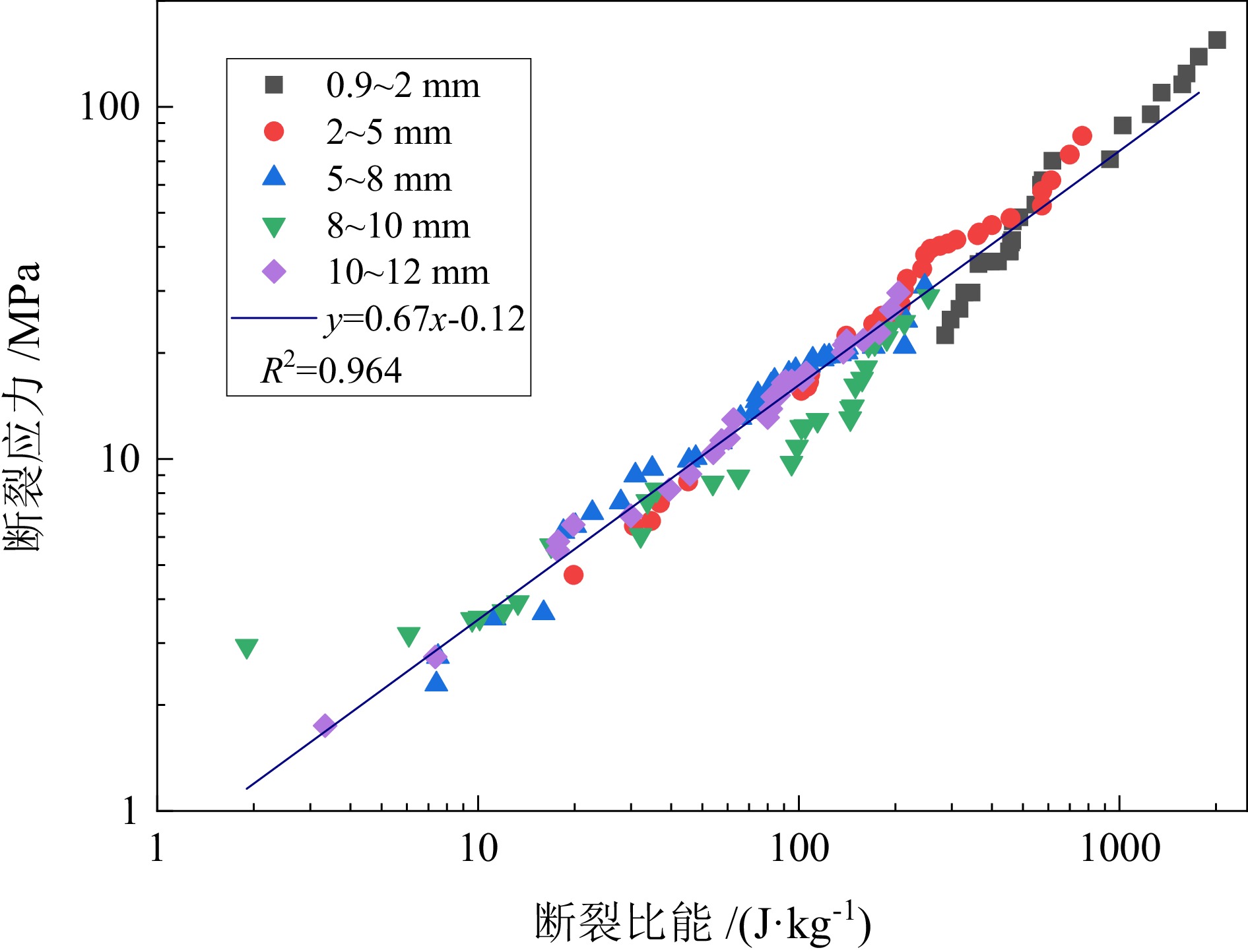
不规则矿石颗粒的断裂是矿物加工过程中常见的现象,其强度分布决定了矿石破碎特性。为了定量分析不规则颗粒的强度分布,通过对5种不同粒级的铜钼矿颗粒进行准静态单轴压缩实验,确定破碎过程中的最大破碎力和断裂能。选取3种常见的统计学模型分别对不同定义下的(最大破碎力、断裂应力、断裂能和断裂比能)颗粒强度进行拟合,并研究了其与颗粒尺寸和材料特性之间的定量关系。试验结果表明:Weibull模型较Lognormal和Lmogintic两种模型更适合描述铜钼矿颗粒的强度分布,其模型中强度分布的离散程度D只与材料特性有关,与颗粒尺寸呈弱函数关系;F63.20、E63.20与颗粒尺寸呈正比关系,而σ63.20和Em63.20随着颗粒尺寸的增大呈幂函数规律减小;不同定义下的颗粒强度之间(最大破碎力−断裂能和断裂应力−断裂比能)的关系都只与材料特性有关,而与颗粒尺寸无关,在双对数坐标系下斜率分别为1.49与0.67。
Abstract:The fracture of irregular ore particles is a common phenomenon in mineral processing. The strength distribution of particles determines the crushing characteristics of ore. In order to quantitatively analyze the strength distribution of irregular particles, the maximum crushing force and fracture energy in the crushing process were determined by quasi−static uniaxial compression tests on five different sizes of copper−molybdenum ore particles. Three common statistical models were selected to fit the particle strength under different definitions(crushing force, crushing stress, breakage energy and breakage specific energy), and their quantitative relationships with particle size and material properties were studied. The test results show that the Weibull model was more suitable for describing the strength distribution of copper−molybdenum ore particles than the other two models. The dispersion degree D of the strength distribution in the model was related to the material properties and had a weak function relationship with the particle size. F63.20 and E63.20 were proportional to the particle size, while σ63.20 and Em63.20 decreased with the increase of particle size in a power function law. The relationship between particle strength (maximum breaking force−breaking energy and stress−breaking specific energy) under different definitions is only related to material properties, not particle size. The slopes were 1.49 and 0.67 in the double logarithmic coordinate system, respectively.
-
Key words:
- irregular particles /
- particle strength distribution /
- select function /
- weibull model
-

-
表 1 部分试验数据拟合的相关系数
Table 1. Correlation coefficient fitted to some experimental data
类型 模型 R2 最大破碎力 Logistic 0.984 Lognormal 0.981 Weibull 0.989 断裂应力 Logistic 0.984 Lognormal 0.981 Weibull 0.989 断裂能 Logistic 0.979 Lognormal 0.981 Weibull 0.990 断裂比能 Logistic 0.979 Lognormal 0.981 Weibull 0.990 表 2 不同粒级的铜钼矿颗粒强度分布拟合离散程度汇总
Table 2. Summary of the degree to which the intensity distribution fits discretely for copper−molybdenum ore particles of different sizes
粒级/mm DF Dσ DE DEm 0.9~2 1.66 1.66 1.51 1.51 2~5 1.62 1.62 1.25 1.25 5~8 1.95 1.95 1.18 1.18 8~10 1.52 1.52 0.95 0.95 10~12 1.87 1.87 1.30 1.30 平均值 1.72 1.72 1.24 1.24 表 3 DF、DE与颗粒尺寸的关系
Table 3. The relationship of DF、DE and particle size
粒级/mm 最大破碎力 /N 断裂能 /J DF F50 R2 DF F50 R2 DE E50 R2 DE E50 R2 0.9~2 1.66 109.14 0.945 1.72 108.35 0.944 1.51 27.79 0.881 1.23 30.08 0.873 2~5 1.62 349.06 0.990 1.72 347.36 0.989 1.25 145.30 0.989 1.23 145.76 0.989 5~8 1.95 557.38 0.964 1.72 559.27 0.960 1.18 430.10 0.989 1.23 429.21 0.988 8~10 1.52 902.90 0.990 1.72 893.58 0.985 0.95 911.01 0.943 1.23 928.01 0.926 10~12 1.87 1317.51 0.985 1.72 1306.47 0.983 1.30 1366.01 0.980 1.23 1373.01 0.980 -
[1] FUERSTENAU D W, ABOUZEID A Z M. The energy efficiency of ball milling in comminution[J]. International Journal of Mineral Processing, 2002, 67(1): 161−185.
[2] TAVARES L M. Handbook of Powder Technology[M]. Oxford: Elsevier, 2007: 3−68.
[3] POWELL M S, MORRISON R D. The future of comminution modelling[J]. International Journal of Mineral Processing, 2007, 84(1/2/3/4): 228−239. doi: 10.1016/j.minpro.2006.08.003
[4] VOGEL L, PEUKERT W. Breakage behaviour of different materials−construction of a mastercurve for the breakage probability[J]. Powder Technology, 2003, 129(1/2/3): 101−110. doi: 10.1016/S0032-5910(02)00217-6
[5] SALMAN, ALEXANDER RUSSELL, SERGEJ AMAN, et al. Breakage probability of granules during repeated loading[J]. Powder Technology, 2015, 269: 541−547. doi: 10.1016/j.powtec.2014.09.044
[6] AMAN S, JüRGEN T, KALMAN H. Breakage probability of irregularly shaped particles[J]. Chemical Engineering Science, 2010, 65(5): 1503−1512. doi: 10.1016/j.ces.2009.10.016
[7] 刘建远. 威布尔分布在颗粒碎裂描述和粉碎数学建模中的应用[J]. 矿冶, 2009(3): 1−8. doi: 10.3969/j.issn.1005-7854.2009.03.001
LIU J Y. Application of Weibull distribution in particle fragmentation description and comminution mathematical modeling[J]. Mining and Metallurgy, 2009(3): 1−8. doi: 10.3969/j.issn.1005-7854.2009.03.001
[8] ROZENBLAT Y, PORTNIKOV D, LEVY A, et al. Strength distribution of particles under compression[J]. Powder Technology, 2011, 208(1): 215−224. doi: 10.1016/j.powtec.2010.12.023
[9] HUANG J, XU S, YI H, HU S. Size effect on the compression breakage strengths of glass particles[J]. Powder Technology, 2014, 268(1): 86−94.
[10] GHADIRI M, BRUNARD N, KOLENDA F. Weibull analysis of quasistatic crushing strength of catalyst particles[J]. Chemical Engineering Research & Design, 2003, 81(8): 953−962.
[11] PETUKHOV Y, KALMAN H. Empirical breakage ratio of particles due to impact[J]. Powder Technology, 2004, 143(26): 160−169.
[12] JüRGEN T, SCHREIER M, TORSTEN G. Impact crushing of concrete for liberation and recycling[J]. Powder Technology, 1999, 105(1): 39−51.
[13] LIN Y L, WANG D M, LU W M. Compression and deformation of soft spherical particles[J]. Chemical Engineering Science, 2008, 63(1): 195−203. doi: 10.1016/j.ces.2007.09.028
[14] ANTONYUK S, TOMAS J, HEINRICH S. Breakage behaviour of spherical granulates by compression[J]. Chemical Engineering Science, 2005, 60(14): 4031−4044. doi: 10.1016/j.ces.2005.02.038
[15] WEICHERT R. Theoretical prediction of energy consumption and particle size distribution in grinding and drilling of brittle materials[J]. Particle & Particle Systems Characterization, 1991, 8(1): 55−62.
[16] MA L, LI Z, WANG M. Effects of size and loading rate on the mechanical properties of single coral particles[J]. Powder Technology, 2019, 342: 961−971. doi: 10.1016/j.powtec.2018.10.037
[17] 黄俊宇. 冲击载荷下脆性颗粒材料多尺度变形破碎特性研究[D]. 合肥: 中国科学技术大学, 2016.
HUANG J Y. Research on multi−scale deformation and breakage characteristics of brittle particle materials under impact load[D]. Hefei: University of Science and Technology of China, 2016.
[18] 周强, 潘永泰, 朱长勇, 等. 准静态下脆性材料强度分布试验研究[J]. 煤炭学报, 2019, 44(S2): 708−716.
ZHOU Q, PAN Y T, ZHU C Y, et al. Experimental study on strength distribution of brittle materials at quasistatic state[J]. Journal of China Coal Society, 2019, 44(S2): 708−716.
-




 下载:
下载: