低渗储层岩石物理建模新方法及其在东海Z气田中的应用

李炳颖; 涂齐催; 刘江; 娄敏; 张佳佳; 黄鑫; 王腊梅

doi:10.16028/j.1009-2722.2023.009

低渗储层岩石物理建模新方法及其在东海Z气田中的应用

1.
中海石油（中国）有限公司上海分公司，上海 200335

2.
中国石油大学（华东）地球科学与技术学院，青岛 266580

基金项目: 国家自然科学基金“东海深层低渗-致密气储层体系质量差异性成因机制及演化模式”（41672129、41602135）；中海石油（中国）有限公司重大科技项目“西湖凹陷在生产油气田中后期综合调整关键技术研究与实践”（CNOOC-KJ135ZDXM39SH03）

详细信息

作者简介: 李炳颖（1987—），男，硕士，高级工程师，主要从事油气田开发地震方面的研究工作. E-mail：liby9@cnooc.com.cn

通讯作者: 娄敏（1993—），男，硕士，工程师，主要从事地震解释和储层方面的研究工作. E-mail：loumin2@cnooc.com.cn

中图分类号: P744.4；P618.13

收稿日期: 2023-01-09

刊出日期: 2024-02-28

A new method of rock physics modeling and its application in low permeability reservoirs of Z Gasfield, East Sea Basin

1.
Shanghai Branch of CNOOC (China) Ltd., Shanghai 200335, China

2.
School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China

More Information

Corresponding author: LOU Min, loumin2@cnooc.com.cn

Received Date: 09 January 2023

Publish Date: 28 February 2024

摘要

摘要:
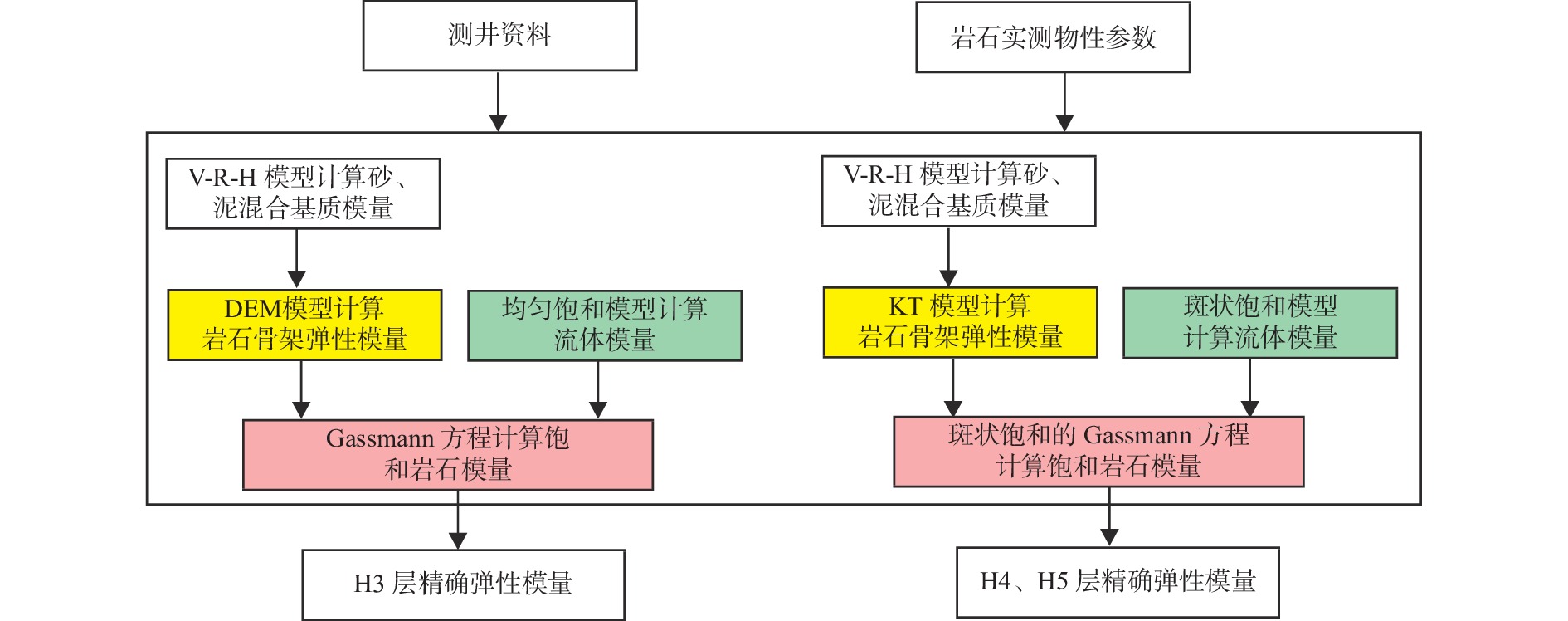
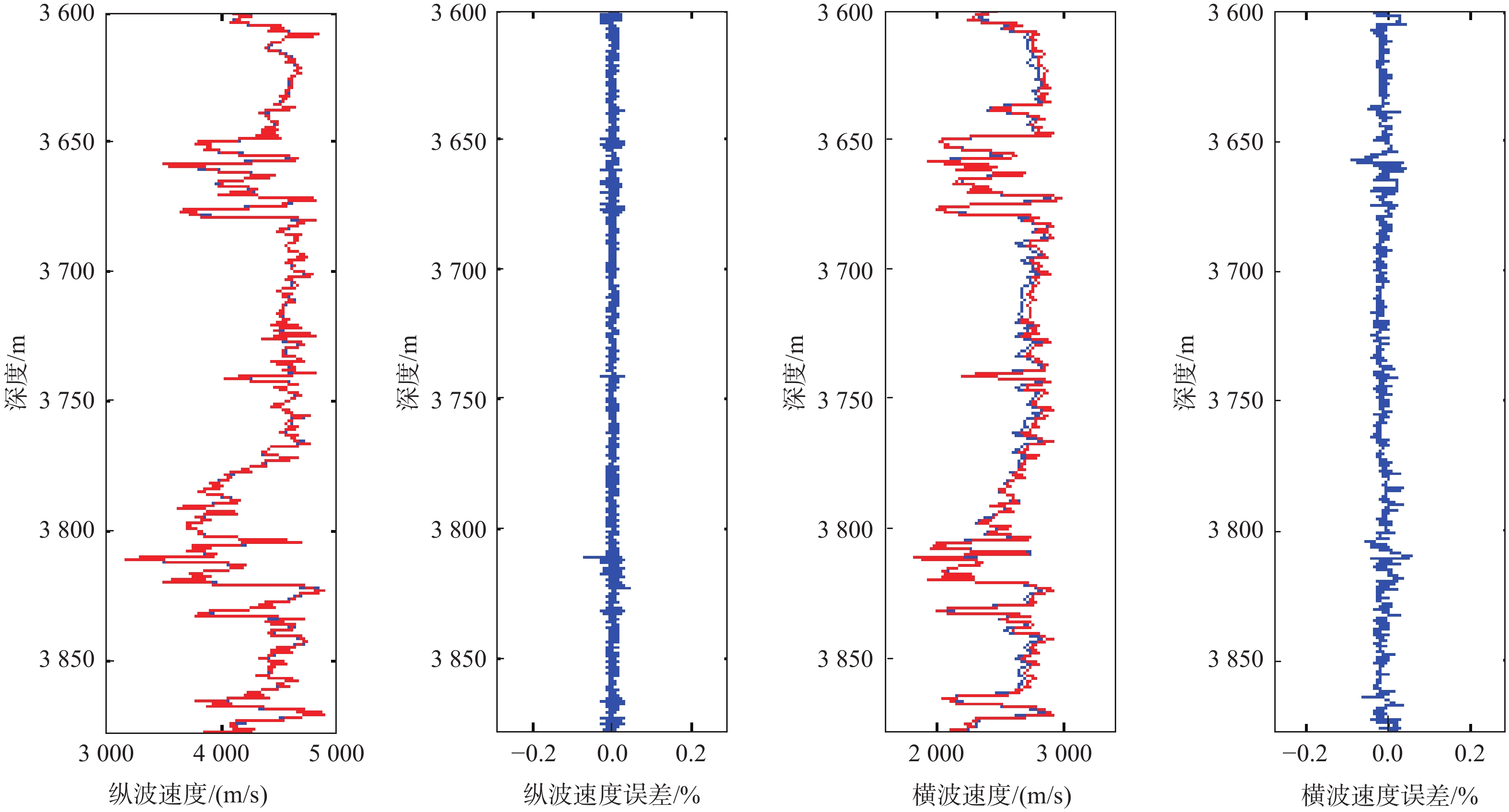
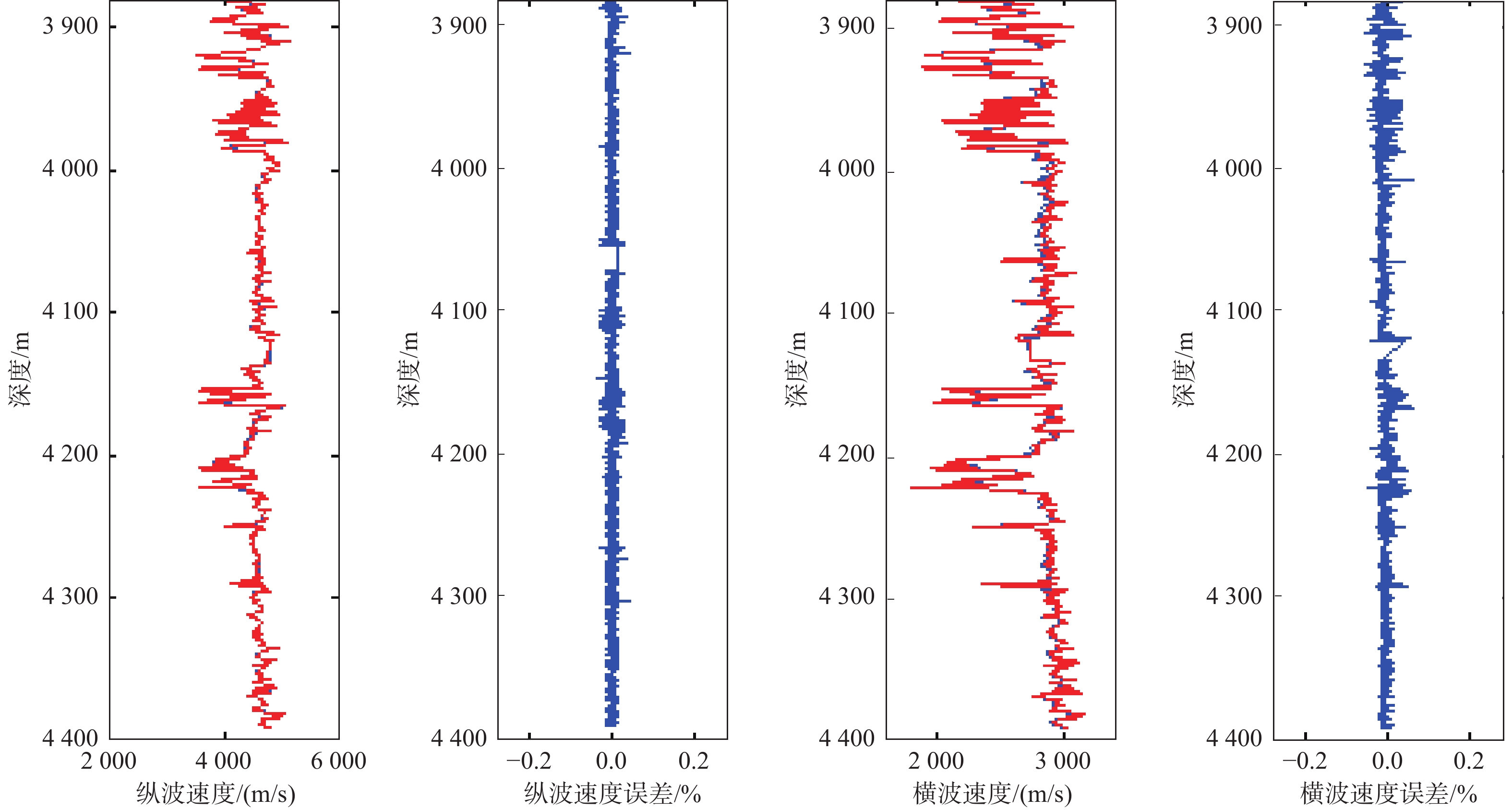
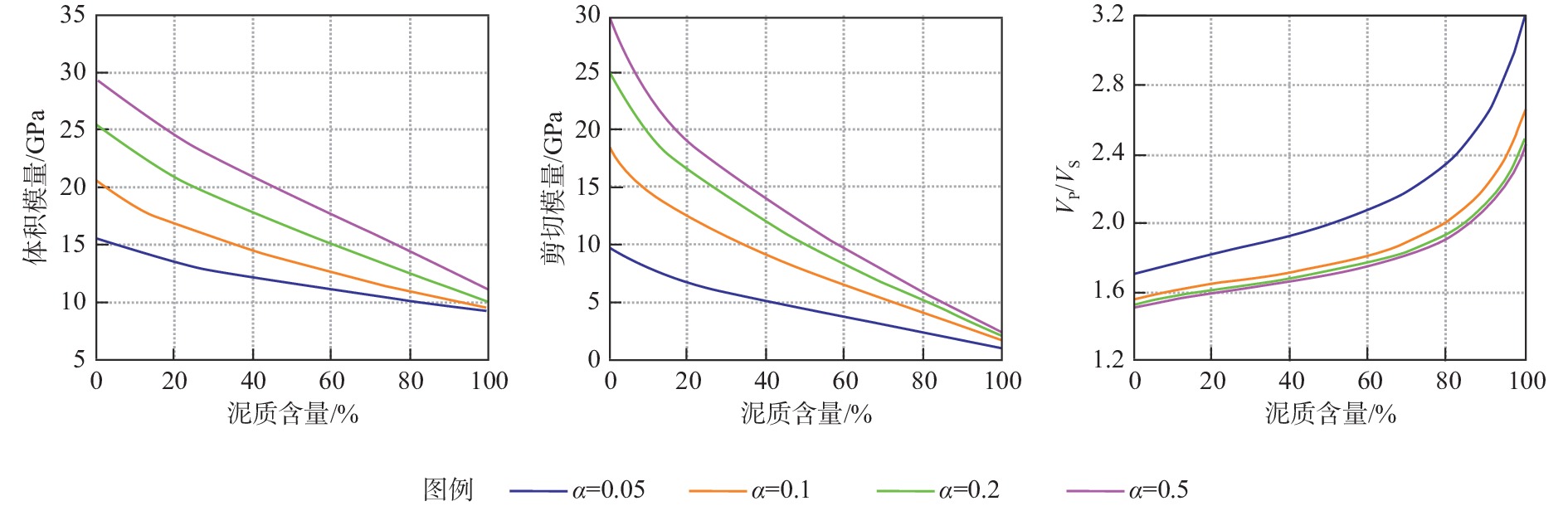
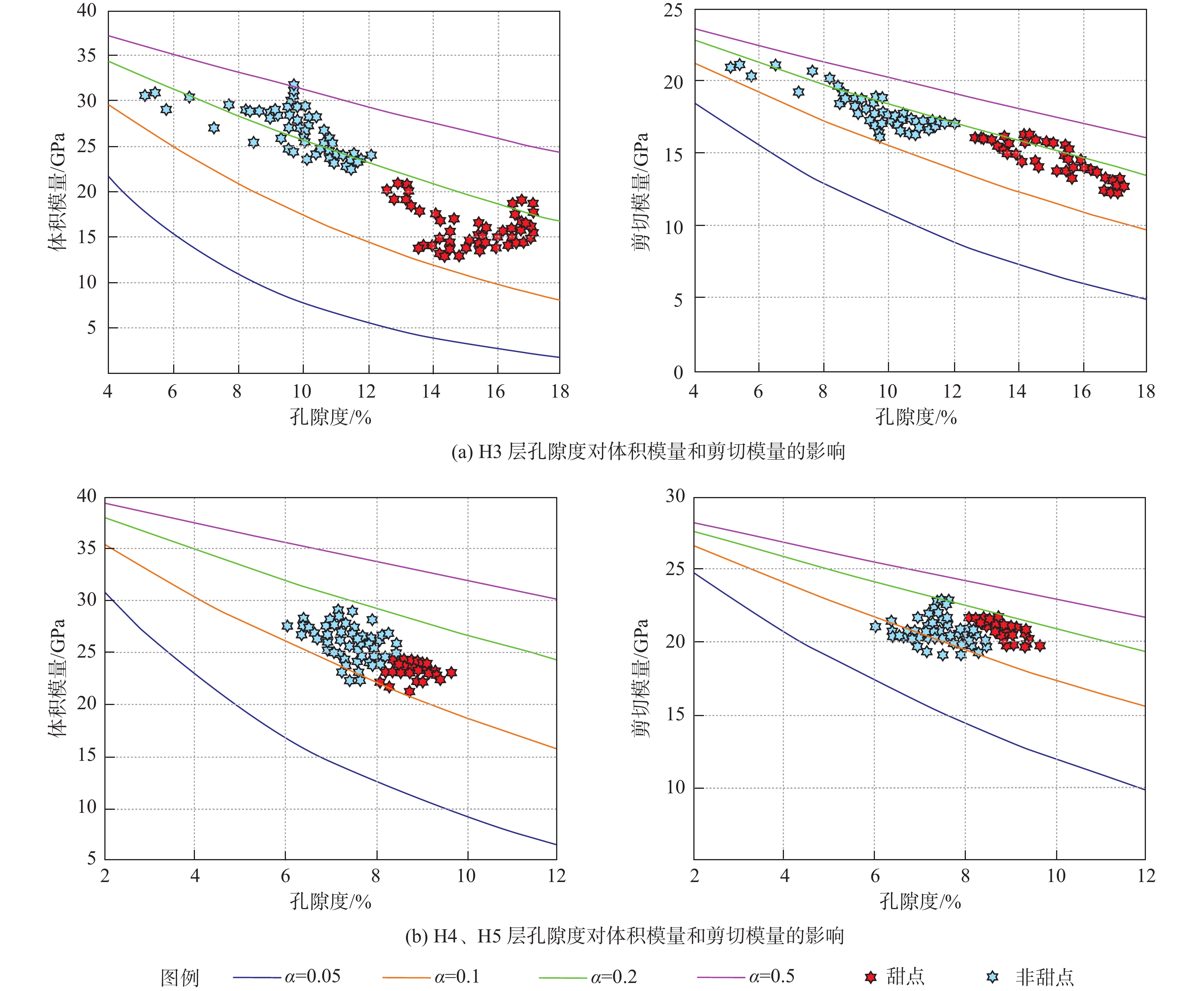
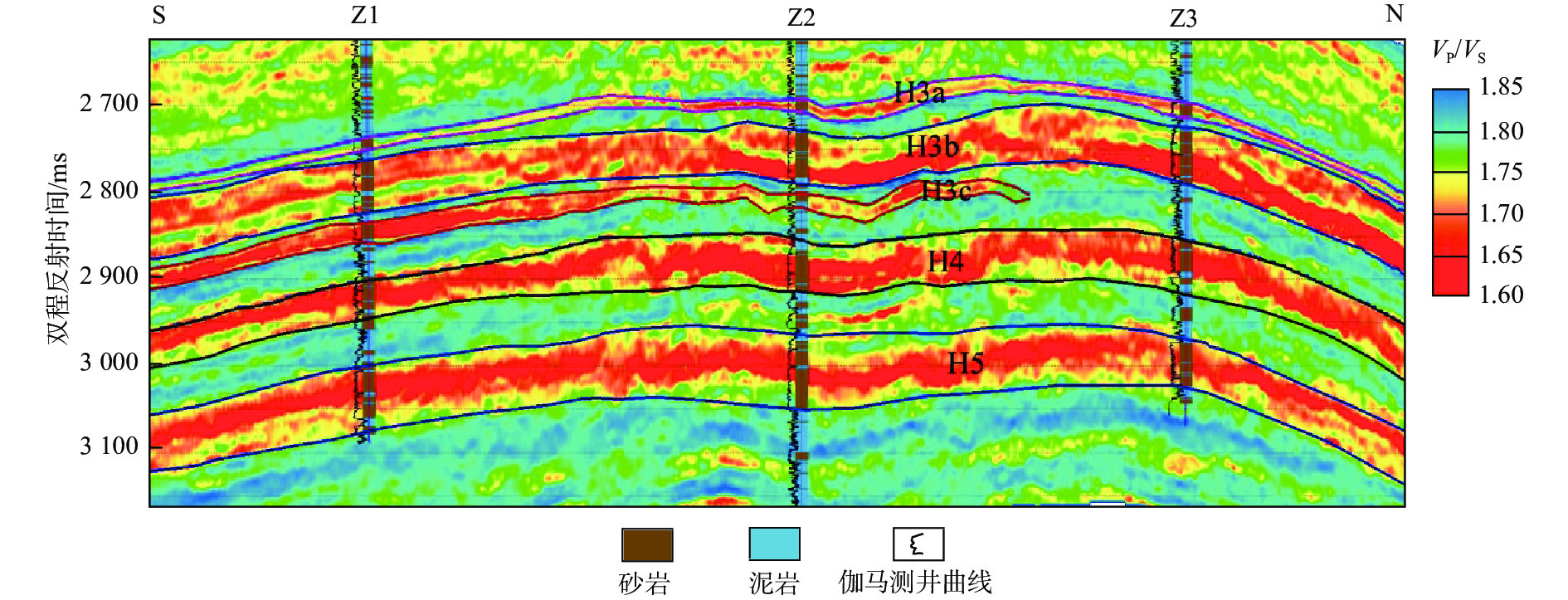
低渗储层孔隙结构复杂，非均质性强，不同类型低渗储层之间也常存在较大物性变化，难以采用统一的岩石物理模型表征储层参数与弹性参数之间的关系。针对上述难题，提出了低渗储层分层岩石物理建模方法：针对中低孔-中低渗储层采用基于DEM理论的流体均匀饱和模型；针对特低孔、特低渗储层采用基于KT理论的流体非均匀饱和模型。基于分层岩石物理建模预测的纵、横波速度与测井真实速度吻合较好，验证了该方法的可靠性。在建立准确岩石物理模型的基础上，进一步分析了弹性参数受泥质含量、孔隙度、孔隙形状等因素影响的变化规律，从而指导低渗储层的岩性及“甜点”预测。
- 低渗储层 /
- 孔隙结构 /
- 岩石物理建模 /
- 弹性参数 /
- 体积模量 /
- 剪切模量
Abstract:
Low-permeability reservoirs have complex pore structure characteristics for which conventional petrophysical modeling methods are not suitable for detection. In addition, physical properties among different layers of low-permeability reservoirs vary considerably, so it is difficult to use unified petrophysical model to characterize the relationship between reservoir parameters and elastic parameters. We proposed a new technical approach to stratified rock physics modeling of low permeability reservoirs: for medium-low porosity and medium-low permeability reservoirs, the fluid uniform saturation model based on DEM theory was adopted; for extra-low porosity and extra-low permeability reservoirs, the fluid non-uniform saturation model based on KT theory was adopted. The predicted P-wave and S-wave velocities based on stratified rock physical modeling were in good agreement with the real logging data, which verified the reliability of the method. Based on the accurate petrophysical models, the laws of elastic parameters variations with shale content, porosity, and pore shape were further analyzed, to guide the prediction of lithology and "sweet spot" in low permeability reservoir.
- low permeability reservoir /
- pore structure /
- rock physics modeling /
- elastic parameter /
- bulk modulus /
- shear modulus

HTML全文

图 1 研究区花港组地层岩芯孔隙度和渗透率分布

Figure 1.

下载: 全尺寸图片幻灯片

图 2 低渗储层分层岩石物理建模技术流程

Figure 2.

下载: 全尺寸图片幻灯片

图 3 研究区H3层纵、横波速度重构结果

Figure 3.

下载: 全尺寸图片幻灯片

图 4 研究区H4、H5层纵、横波速度重构结果

Figure 4.

下载: 全尺寸图片幻灯片

图 5 泥质含量对岩石体积模量、剪切模量及纵、横波速度比的影响

Figure 5.

下载: 全尺寸图片幻灯片

图 6 纵波阻抗与纵、横波速度比的测井岩石物理交汇

Figure 6.

下载: 全尺寸图片幻灯片

图 7 孔隙度对岩石体积模量和剪切模量的影响

Figure 7.

下载: 全尺寸图片幻灯片

图 8 研究区H3—H5层基于V_P/V_S 反演的岩性预测剖面

Figure 8.

下载: 全尺寸图片幻灯片

图 9 研究区H3层基于剪切模量反演的“甜点”预测剖面

Figure 9.

下载: 全尺寸图片幻灯片

参考文献(24)

[1]	欧阳健. 加强岩石物理研究提高油气勘探效益[J]. 石油勘探与开发,2001,28(2):1-5.
[2]	马淑芳,韩大匡,甘利灯,等. 地震岩石物理模型综述[J]. 地球物理学进展,2010,25(2):460-471.
[3]	BATZLE M,WANG Z. Seismic properties of pore fluids[J]. Geophysics,1992,57(1):1396-1468.
[4]	印兴耀,刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探,2016,55(3):309-325.
[5]	姜仁,曾庆才,黄家强,等. 岩石物理分析在叠前储层预测中的应用[J]. 石油地球物理勘探,2014,49(2):322-328.
[6]	刘军,刘杰,曹均,等. 基于岩石物理实验的储层与孔隙流体敏感参数特征:以珠江口盆地东部中—深层碎屑岩储层为例[J]. 石油学报,2019,40(S1):197-205.
[7]	张益明,秦小英,郭智奇,等. 针对致密砂岩气储层复杂孔隙结构的岩石物理模型及其应用[J]. 吉林大学学报(地球科学版),2021,51(3):927-939.
[8]	王震宇,刘俊州. 岩石物理建模技术在致密砂岩储层预测中的应用:以鄂尔多斯盆地北部H区块为例[J]. 物探化探计算技术,2019,41(1):34-40.
[9]	陈昌. 叠前地震反演在清水地区砂砾岩优质储层预测中的应用[J]. 海洋地质前沿,2017,33(6):59-64.
[10]	肖张波,雷永昌,邱欣卫,等. 泊松阻抗属性在陆丰南古近系低渗砂岩储层“甜点”识别中的应用[J]. 海洋地质前沿,2022,38(6):70-77.
[11]	姜雨,涂齐催. 利用岩石物理分析及叠前反演技术解决致密砂岩气储层预测问题:以西湖凹陷A区块为例[J]. 海洋地质前沿,2015,31(11):36-42.
[12]	印兴耀,刘倩. 致密储层各向异性地震岩石物理建模及应用[J]. 中国石油大学学报(自然科学版),2016,40(2):52-58.
[13]	张龙海,刘忠华,周灿灿,等. 低孔低渗储集层岩石物理分类方法的讨论[J]. 石油勘探与开发,2008,35(6):763-768.
[14]	李芳,邓勇,胡林,等. 地球物理技术预测莺歌海盆地低孔低渗储层孔隙度[J]. 地质科技通报,2022,41(4):84-90.
[15]	杨志芳,曹宏,姚逢昌,等. 复杂孔隙结构储层地震岩石物理分析及应用[J]. 中国石油勘探,2014,19(3):50-56.
[16]	BIOT M A. Theory of propagation of elastic waves in a fluid saturated porous solid[J]. Journal of the Acoustical Society of America,1956,28(2):168-191. doi: 10.1121/1.1908239
[17]	XU S,WHITE R. A new velocity model for clay-sand mixtures[J]. Geophysical prospecting,1995,43(1):91-118. doi: 10.1111/j.1365-2478.1995.tb00126.x
[18]	MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook: tools for seismic analysis of porous media[M]. Cambridge: Cambridge University Press, 2009.
[19]	KUSTER G T,TOKSÖZ M N. Velocity and attenuation of seismic waves in two-phase media:part I. theoretical formulations[J]. Geophysics,1974,39(5):587-606. doi: 10.1190/1.1440450
[20]	BERRYMAN J G. Long‐wavelength propagation in composite elastic media I. spherical inclusions[J]. The Journal of the Acoustical Society of America,1980,68:1809-1819. doi: 10.1121/1.385171
[21]	GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics,1951,16(4):673-685. doi: 10.1190/1.1437718
[22]	CIZ R,SHAPIRO S A. Generalization of Gassmann’s equations for porous media saturated with a solid material[J]. Geophysics,2007,72(6):75-79. doi: 10.1190/1.2772400
[23]	印兴耀,刘欣欣,曹丹平. 基于Biot相洽理论的致密砂岩弹性参数计算方法[J]. 石油物探,2013,52(5):445-451.
[24]	HILL R. The elastic behavior of crystalline aggregate[J]. Proceedings of the Physical Society,1952,65:349-354.