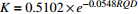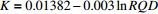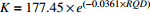A model for estimating hydraulic conductivity of fractured rock mass based on correlation indexes
-
摘要:
掌握岩体的渗透性是精细化描述一个地区水文地质特征的重要工作。渗透系数是表征岩体渗透性的重要指标,研究渗透系数估算模型对于实际工程应用具有重要意义。在现有的渗透系数估算模型中,单因子模型忽略了其他因素对该地区渗透系数的综合影响,复合因子模型存在参数选取不够灵活、部分参数较难获取等问题。基于公开数据,分类整理和对比分析了影响裂隙岩体渗透性的正、负相关参数,提出一种拟合效果好、参数选取灵活的渗透系数估算模型——PNC(Positive and Negative Correlation)模型。研究结果表明:在研究区一,PNC模型的拟合效果(可决系数R2=0.964和R2=0.801)优于HC模型的拟合效果(R2=0.905和R2=0.563);在研究区二,PNC模型的拟合效果(R2=0.959)优于RMP模型的拟合效果(R2=0.927);在研究区三,PNC模型的拟合效果(R2=0.94~0.99)优于ZRF模型的拟合效果(R2=0.92~0.99)。利用纳什效率系数(Nash-Sutcliffe Coefficient,NSE)进行模型误差分析,7组数据中有5组数据的误差系数在0.95以上。这说明PNC模型具有便利性和可靠性,可以为实际工程估算和验证渗透系数提供一定的参考。
Abstract:Mastering hydraulic conductivity of rock mass is an important way to precisely describe hydrogeological characteristics of a certain region. Hydraulic conductivity is a significant indicator to reflect the rock mass’ permeability. The studies of hydraulic conductivity estimation models have important implications for the development of actual engineering. In the existing estimation models of hydraulic conductivity, the single-factor model cannot take into consideration of the comprehensive influence of various factors on hydraulic conductivity in the area, and the parameters selection of the multi-factor model lacks the flexibility and its application is limited when some parameters are difficult to be obtained, etc. The classification and comparative analyses of the positive and negative correlation parameters are conducted based on public data. We propose a set of high-fitting hydraulic conductivity estimation models, which are the PNC (Positive and negative correlation) model. The research results show that the fitting result of the PNC model (R2=0.964 and R2=0.801) is superior to that of the HC model (R2=0.905 and R2=0.563) in No. 1 study area. In No. 2 study area, the fitting result of the PNC model (R2=0.959) is superior to that of the RMP model (R2=0.927). In No. 3 study area, the fitting result of the PNC model (R2=0.94 to 0.99) is also better than that of the ZRF model (R2=0.92 to 0.99). By using Nash-Sutcliffe coefficient (NSE) to carry out the error analyses of the model, it is found that the error coefficients of 5 in 7 sets of data are above 0.95. It further illustrates the convenience and reliability of the PNC model, which can provide a certain reference for estimating and verifying hydraulic conductivity in actual engineering.
-

-
表 1 考虑深度Z的渗透系数估算模型
Table 1. Estimation model of hydraulic conductivity considering depth Z
表 2 复合因子的渗透系数估算模型
Table 2. Multi-factor estimation model of hydraulic conductivity
表 3 岩石质量指标RQD与渗透系数K的拟合方程
Table 3. Fitting equations of RQD and hydraulic conductivity K
表 4 HB-94-01、HB-95-01和HB-95-02相关数据的分类整理与渗透系数拟合
Table 4. Classification of relevant data of borehole HB-95-01, HB-95-01 and HB-95-02
钻孔名称 负相关指标KN 正相关指标KP 渗透系数实测值
K/(10−6cm·s−1)PNC模型的拟合值
K/(10−6cm·s−1)HC模型的拟合值
K/(10−6cm·s−1)岩石质量指标
RQD深度指标
Z/m泥质含量指标
1-GCD岩性渗透性指标
LPIHB-94-01 0.906 35.50 0.999 0.999 7.060 13.700 5.710 0.562 37.20 0.999 0.999 164.000 136.000 43.800 0.937 57.50 0.999 0.950 1.530 0.947 1.930 0.500 75.40 0.999 0.400 5.300 3.050 5.640 0.999 78.00 0.999 0.400 0.042 0.075 0.028 0.875 83.40 0.999 0.400 0.231 0.113 0.618 0.999 91.00 0.999 0.400 0.029 0.034 0.014 0.500 95.00 0.999 0.400 0.453 0.832 1.840 HB-95-01 0.655 100.45 0.200 0.400 0.980 0.832 1.020 0.310 118.65 0.999 0.850 97.600 101.000 57.700 0.276 134.65 0.286 0.999 4.680 6.140 11.400 HB-95-02 0.929 90.00 0.999 0.600 15.600 16.700 2.510 0.969 97.60 0.999 0.600 2.420 12.400 0.770 0.781 120.10 0.071 0.700 0.136 0.186 0.324 0.656 136.40 0.727 0.700 11.700 10.100 13.400 0.062 156.40 0.103 0.700 1.990 2.050 3.170 0.062 174.60 0.103 0.700 0.908 1.760 2.760 0.406 191.40 0.999 0.700 101.000 45.400 29.300 0.464 198.20 0.500 0.999 6.000 6.140 16.100 0.321 214.60 0.999 0.999 45.400 45.400 46.300 0.607 250.40 0.091 0.700 0.403 0.306 0.317 0.786 273.40 0.999 0.700 3.360 6.140 2.620 表 5 ZK10相关数据的分类整理与渗透系数拟合
Table 5. Classification of relevant data and hydraulic conductivity fitting of borehole ZK10
钻孔名称 负相关指标KN 正相关指标KP 渗透系数实测值
K/(10−6cm·s−1)PNC模型的拟合值
K/(10−6cm·s−1)RMP模型的拟合值
K/(10−6cm·s−1)岩石质量指标
RQD岩体完整性指标
RID裂隙宽度指标
AD岩性渗透性指标
LPDZK10 0.870 0.88 1.007 0.15 0.170 0.205 0.172 0.860 0.84 1.231 0.15 0.272 0.277 0.275 0.880 0.87 1.530 0.15 0.242 0.306 0.240 0.870 0.79 0.418 0.15 0.124 0.124 0.128 0.810 0.80 4.244 0.15 1.260 1.240 1.260 0.810 0.80 0.213 0.15 0.100 0.113 0.094 0.540 0.61 3.780 0.15 4.460 6.140 4.350 0.590 0.69 3.961 0.15 4.280 4.330 4.060 0.820 0.73 3.693 0.15 1.350 1.370 1.370 0.530 0.59 3.977 0.15 9.860 1.010 6.900 0.670 0.69 3.623 0.15 3.940 2.760 3.180 0.660 0.67 3.891 0.15 4.980 5.030 3.620 0.690 0.69 3.354 0.15 2.190 2.260 2.290 0.840 0.83 3.566 0.15 0.816 0.832 0.808 0.820 0.82 3.920 0.15 1.050 1.020 1.040 表 6 PNC模型与ZRF模型拟合结果对比
Table 6. Comparison of the fitting results between the PNC model and the ZRF model
钻孔名称 
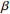
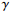
PNC模型拟合的R2 ZRF模型拟合的R2 ZK343 2.937 −5.637 16.030 0.94 0.92 ZK204 −9.118 −0.780 −7.083 0.99 0.99 ZK223 9.857 −1.281 −4.927 0.97 0.94 ZK153 1.330 −1.921 −2.241 0.96 0.95 表 7 纳什效率系数误差分析
Table 7. The NSE error analyses
钻孔名称 ferror HB-94-01 0.95 HB-95-01和HB-95-02 0.70 ZK10 0.96 ZK343 0.90 ZK204 0.98 ZK223 0.97 ZK153 0.96 -
[1] BEAR J. Dynamics of fluids in porous media[M]. New York: American Elsevier Publication Company, 1972.
[2] 马婧, 鲁春辉, 吴吉春, 等. 一种可增加海岛地下淡水资源储量的方法研究[J]. 水文地质工程地质,2020,47(3):1 − 7. [MA Jing, LU Chunhui, WU Jichun, et al. A method for improving the fresh groundwater storage of oceanic islands[J]. Hydrogeology & Engineering Geology,2020,47(3):1 − 7. (in Chinese with English abstract)
[3] 樊贵超, 钟登华, 任炳昱, 等. 基于分形理论的坝基裂隙岩体注灰量与导水率关系研究[J]. 水利学报,2017,48(5):576 − 587. [FAN Guichao, ZHONG Denghua, REN Bingyu, et al. Research on the relationship between cement take and transmissivity of fractured rocks under dam foundation based on fractal theory[J]. Journal of Hydraulic Engineering,2017,48(5):576 − 587. (in Chinese with English abstract)
[4] 杜欣, 曾亚武, 唐冬云. 基于水下抽水试验的岩体渗透系数研究及应用[J]. 岩石力学与工程学报,2010,29(增刊2):3542 − 3548. [DU Xin, ZENG Yawu, TANG Dongyun. Research on permeability coefficient of rock mass based on underwater pumping test and its application[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(Sup2):3542 − 3548. (in Chinese with English abstract)
[5] QUINN P M, PARKER B L, CHERRY J A. Using constant head step tests to determine hydraulic apertures in fractured rock[J]. Journal of Contaminant Hydrology,2011,126(1/2):85 − 99.
[6] 张必昌, 胡成, 陈刚, 等. 利用电导率测井与压水试验联合评价岩体渗透性的方法[J]. 水文地质工程地质,2019,46(3):62 − 69. [ZHANG Bichang, HU Cheng, CHEN Gang, et al. Method of evaluating the permeability of rock mass by the combination of packer test and flowing fluid electrical conductivity log[J]. Hydrogeology & Engineering Geology,2019,46(3):62 − 69. (in Chinese with English abstract)
[7] 翟晓荣, 吴基文, 韩东亚. 补给边界群孔放水试验的含水层参数计算[J]. 中国矿业大学学报,2014,43(5):837 − 840. [ZHAI Xiaorong, WU Jiwen, HAN Dongya. Aquifer parameter calculation of pumping test of group holes with recharge boundary[J]. Journal of China University of Mining & Technology,2014,43(5):837 − 840. (in Chinese with English abstract)
[8] XU J P, CHEN M Y, HONG H, et al. Differences of hydraulic conductivities from pumping and draining tests with intensity effects[J]. Journal of Hydrology,2019,579(9):1 − 10.
[9] 尹尚先, 徐斌, 徐慧, 等. 化学示踪连通试验在矿井充水条件探查中的应用[J]. 煤炭学报,2014,39(1):129 − 134. [YIN Shangxian, XU Bin, XU Hui, et al. The application of chemical tracer experiments on exploring the mine water filling conditions[J]. Journal of China Coal Society,2014,39(1):129 − 134. (in Chinese with English abstract)
[10] 李亚美, 成建梅, 崔莉红, 等. 分层监测孔现场分级联合试验确定含水层参数[J]. 南水北调与水利科技,2013,11(3):132 − 137. [LI Yamei, CHENG Jianmei, CUI Lihong, et al. Determination of aquifer parameters from comprehensive in situ pumping and tracing test in the multi-layer monitoring boreholes[J]. South-to-North Water Transfers and Water Science & Technology,2013,11(3):132 − 137. (in Chinese with English abstract)
[11] LOUIS C. Rock hydraulics [M]. Muller L. Vienna: Springer Verlag, 1974: 299-387.
[12] BLACK J H. Flow and flow mechanisms in crystalline rock[J]. Geological Society,1987,34(1):185 − 200. doi: 10.1144/GSL.SP.1987.034.01.13
[13] SNOW D T. The frequency and apertures of fractures in rock[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1970,7(1):23 − 40.
[14] WEI Z Q, EGGER P, DESCOEUDRES F. Permeability predictions for jointed rock masses[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1995,32(3):251 − 261.
[15] CARLSSON A, OLSSON T. Hydraulic properties of Swedish crystalline rocks-hydraulic conductivity and its relation to depth[J]. Bulletin of the Geological Institute,1977(7):71 − 84.
[16] CHEN Y F, LING X M, LIU M M, et al. Statistical distribution of hydraulic conductivity of rocks in deep-incised valleys, Southwest China[J]. Journal of Hydrology,2018,566(9):216 − 226.
[17] 蒋小伟, 万力, 王旭升, 等. 利用RQD估算岩体不同深度的平均渗透系数和平均变形模量[J]. 岩土力学,2009,30(10):3163 − 3167. [JIANG Xiaowei, WAN Li, WANG Xusheng, et al. Estimation of depth-dependent hydraulic conductivity and deformation modulus using RQD[J]. Rock and Soil Mechanics,2009,30(10):3163 − 3167. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2009.10.047
[18] HSU S M, CHUNG M C, CHENG Y K, et al. A rock mass classification scheme for estimating hydraulic conductivity of fractured rocks[C]//Geocongress 2008. Reston: American Society of Civil Engineers, 2008 : 452-459.
[19] KU C Y, HSU S M, CHIOU L B, et al. An empirical model for estimating hydraulic conductivity of highly disturbed clastic sedimentary rocks in Taiwan[J]. Engineering Geology,2009,109(3/4):213 − 223.
[20] 宋琨, 晏鄂川, 陈刚. 地下水封洞库岩体渗透系数估算研究[J]. 岩石力学与工程学报,2014,33(3):575 − 580. [SONG Kun, YAN Echuan, CHEN Gang. Hydraulic conductivity estimation of rock mass in water sealed underground storage caverns[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(3):575 − 580. (in Chinese with English abstract)
[21] 陈君, 刘明明, 李星, 等. 一种基于地质指标的裂隙岩体渗透系数估算模型[J]. 岩土力学,2016,37(6):1706 − 1714. [CHEN Jun, LIU Mingming, LI Xing, et al. A geological indexes-based empirical model for estimation of permeability coefficient in fractured rock mass[J]. Rock and Soil Mechanics,2016,37(6):1706 − 1714. (in Chinese with English abstract)
[22] 中华人民共和国建设部. 中华人民共和国国家标准: 工程岩体分级标准: GB 50218—1994[S]. 北京: 中国标准出版社, 1995.
Ministry of Construction of the People's Republic of China. National Standard (Mandatory) of the People's Republic of China: Standard for engineering classification of rock masses: GB 50218—1994[S]. Beijing: Standards Press of China, 1995. (in Chinese)
[23] 蔡海兵, 程桦. 基于FDAHP理论的深部岩体分级方法[J]. 水文地质工程地质,2012,39(6):43 − 49. [CAI Haibing, CHENG Hua. Classification method of deep rock mass based on FDAHP theory[J]. Hydrogeology & Engineering Geology,2012,39(6):43 − 49. (in Chinese with English abstract)
[24] 陈剑平, 范建华, 刘迪. RQD应用与研究的回顾与展望[J]. 岩土力学,2005,26(增刊2):249 − 252. [CHEN Jianping, FAN Jianhua, LIU Di. A review and prospect on the application and research of RQD[J]. Rock and Soil Mechanics,2005,26(Sup2):249 − 252. (in Chinese with English abstract)
[25] 陈康达, 宋彦辉, 巨广宏, 等. 坝体岩体岩石质量指标、波速和透水率的关系: 以青海玛沁地区玛尔挡水电站为例[J]. 地球科学与环境学报,2018,40(6):822 − 827. [CHEN Kangda, SONG Yanhui, JU Guanghong, et al. Relationships among rock quality designation, wave velocity and permeability of dam foundation rock mass: Taking Maerdang hydropower station in Maqin Area of Qinghai, China as an example[J]. Journal of Earth Sciences and Environment,2018,40(6):822 − 827. (in Chinese with English abstract) doi: 10.3969/j.issn.1672-6561.2018.06.012
[26] QURESHI M U, KHAN K M, BESSAIH N, et al. An empirical relationship between in-situ permeability and RQD of discontinuous sedimentary rocks[J]. Electronic Journal of Geotechnical Engineering,2014,19:4781 − 4790.
[27] EL-NAQA A. The hydraulic conductivity of the fractures intersecting Cambrian sandstone rock masses, central Jordan[J]. Environmental Geology,2001,40(8):973 − 982. doi: 10.1007/s002540100266
[28] ÖGE İ F. Assessing rock mass permeability using discontinuity properties[J]. Procedia Engineering,2017,191:638 − 645. doi: 10.1016/j.proeng.2017.05.373
[29] 万力, 蒋小伟, 王旭升. 含水层的一种普遍规律: 渗透系数随深度衰减[J]. 高校地质学报,2010,16(1):7 − 12. [WAN Li, JIANG Xiaowei, WANG Xusheng. A common regularity of aquifers: the decay in hydraulic conductivity with depth[J]. Geological Journal of China Universities,2010,16(1):7 − 12. (in Chinese with English abstract) doi: 10.3969/j.issn.1006-7493.2010.01.002
[30] KRAUSE P, BOYLE D P, BÄSE F. Comparison of different efficiency criteria for hydrological model assessment[J]. Advances in Geosciences,2005,5:89 − 97. doi: 10.5194/adgeo-5-89-2005
[31] PIÑA A, DONADO L D, BLESSENT D, et al. Analysis of the scale-dependence of the hydraulic conductivity in complex fractured media[J]. Journal of Hydrology,2019,569:556 − 572. doi: 10.1016/j.jhydrol.2018.12.006
-



 下载:
下载:
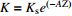
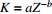
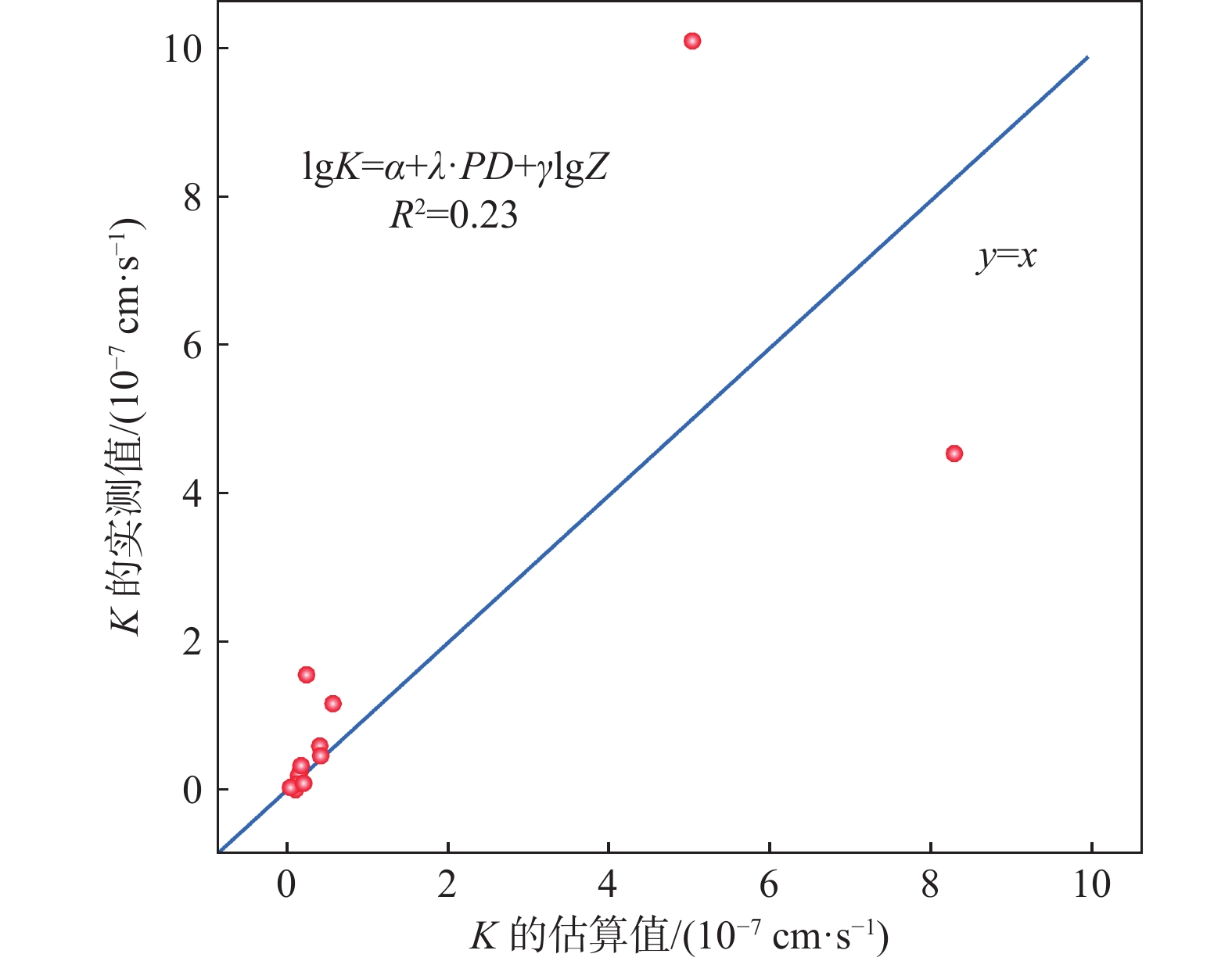
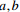 为系数,Z为深度
为系数,Z为深度
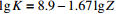
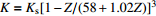
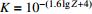
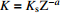
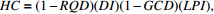
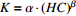
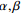 为经验参数
为经验参数
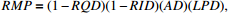
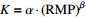
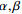 为经验参数
为经验参数
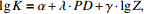

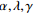 为经验参数
为经验参数