An analysis of direct shear test results of sand - gravel mixture based on the discrete element method
-
摘要:
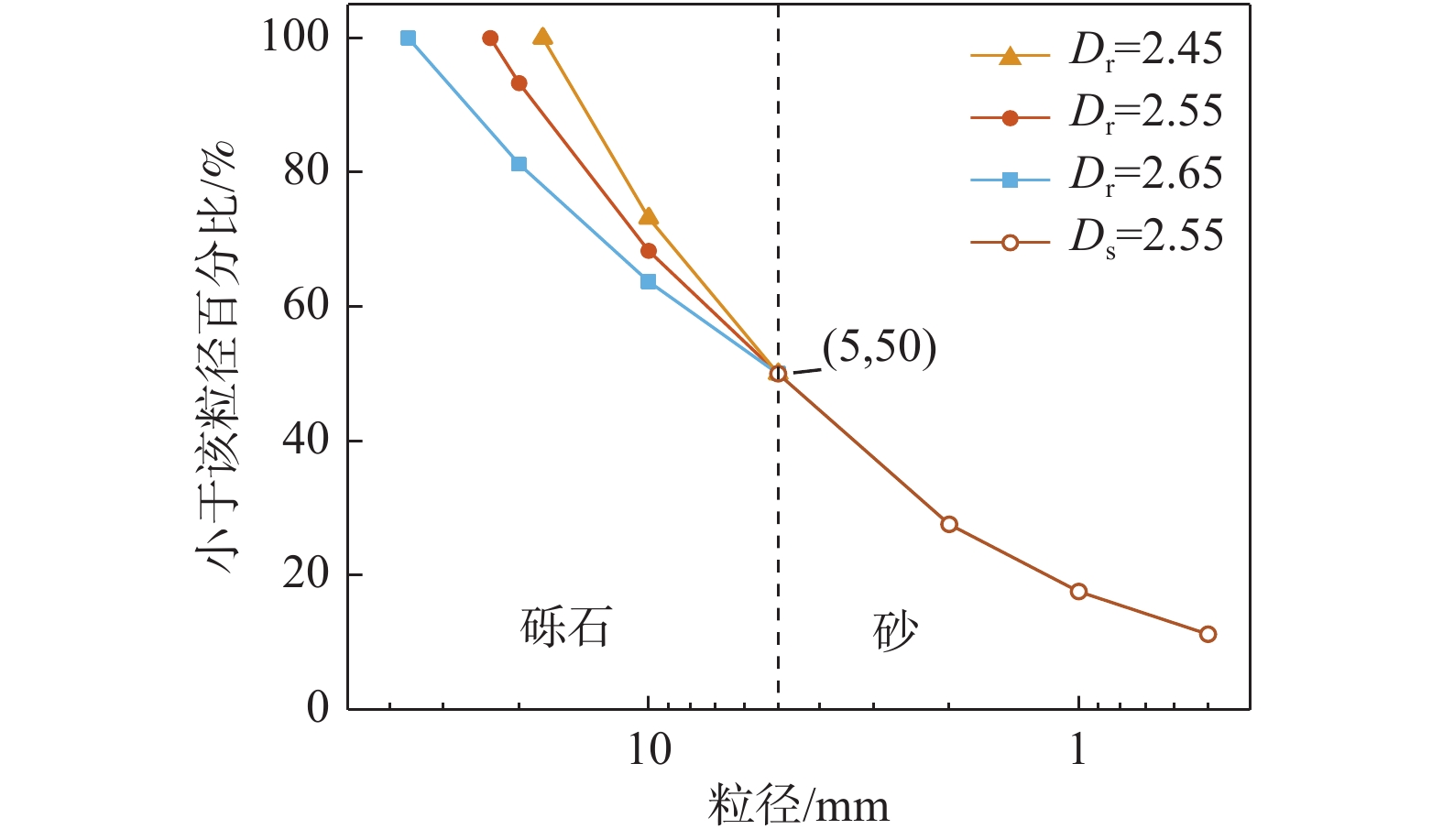
砂石混合体由力学性质以及结构相差极大的材料组成,其组成的重塑地层易发生塌陷等问题,因此对砂石混合体力学特性的研究具有重要的工程意义。砾石形状是砂砾石力学特性研究的重要属性参数,但采用规则图形对砾石进行描述不能反映出其真实的力学性质,采用数字图像处理技术构建的砾石数据库能反映砾石真实形状并可对特定形状参数进行具体分析。由于砂石混合体的粒径分布较广,采用特征粒径等无法描述整体粒度分布,故本文结合分形理论构建砂石混合体的二重分形结构模型,通过粒度分维值反演出完整的级配分布曲线。考虑到砂石混合体离散型的特点,采用离散元软件进行直剪试验数值模拟并对细观结构进行分析,研究结果表明,砂石混合体一般具有2个粒度分维值:砂粒度分维值和砾石粒度分维值,砂、砾石粒度分维值越接近,抗剪强度和内摩擦角越大;当两者相等时,砂石混合体具有一重分维,此时均一性最好,抗剪强度和内摩擦角最大;轴向系数是形容砾石形状的一个重要参数,随着轴向系数的增加,砾石显示出明显的条状性,在直剪试验中抗转动能力增强、周围接触数量增加,导致抗剪强度和内摩擦角不断增加。
Abstract:Sand-gravel mixture is composed of materials with very different mechanical properties and structures, and the remolded strata composed of the sand-gravel mixture are prone to collapse and other problems. Therefore, the research on the mechanical properties of sand-gravel mixture is an urgent problem to be solved. The shape of gravel is an important attribute parameter in the study of the mechanical properties of sand and gravel. Description of gravel with regular graphics cannot reflect its real mechanical properties. In this paper, the gravel database constructed by digital image processing technology can reflect the true shape of gravel and analyse the specific shape parameters. The particle size distribution of the sand-gravel mixture is wide, and the characteristic particle size cannot be used to describe the overall particle size distribution. In this study, combined with the fractal theory, a double fractal model of the sand-gravel mixture is constructed, and the gradation distribution curve is inversed by the particle size fractal dimension value. Taking into account the discrete characteristics of the sand-gravel mixture, the discrete element software is used to carry out the numerical simulation of the direct shear test and analyse the mesostructure. The results indicate that the sand-gravel mixture generally has two particle size fractal dimensions: the coarse sand particle size fractal dimension value and the gravel particle size fractal dimension value. The closer the fractal dimension of sand and gravel particle size is, the greater the shear strength and internal friction angle. When the values are equal, the sand-gravel mixture has 1-D fractal dimension, at this time the uniformity is the best, the shear strength and internal friction angle are the largest. The axial coefficient is an important parameter to describe the shape of gravel. With the increasing axial coefficient, the gravel shows obvious needle-like properties. In the direct shear test, the anti-rotation ability is enhanced and the amount of surrounding contact is increased, leading to the continuous increase of shear stress and internal friction angle.
-

-
表 1 基于离散元模拟的直剪试验主要计算参数
Table 1. Main computational parameters in DEM simulation of direct shear
计算参数 砂 砾石 法向刚度kn/(  )
)5×108 5×109 切向刚度ks/(  )
)2×108 2×109 摩擦系数 0.5 0.9 粒径/mm 0.5~5.0 >5.0 表 2 不同砾石粒度分维值在直剪试验中获取的相关参数
Table 2. Correlation parameters of fractal dimension of different gravel sizes obtained in the direct shear test
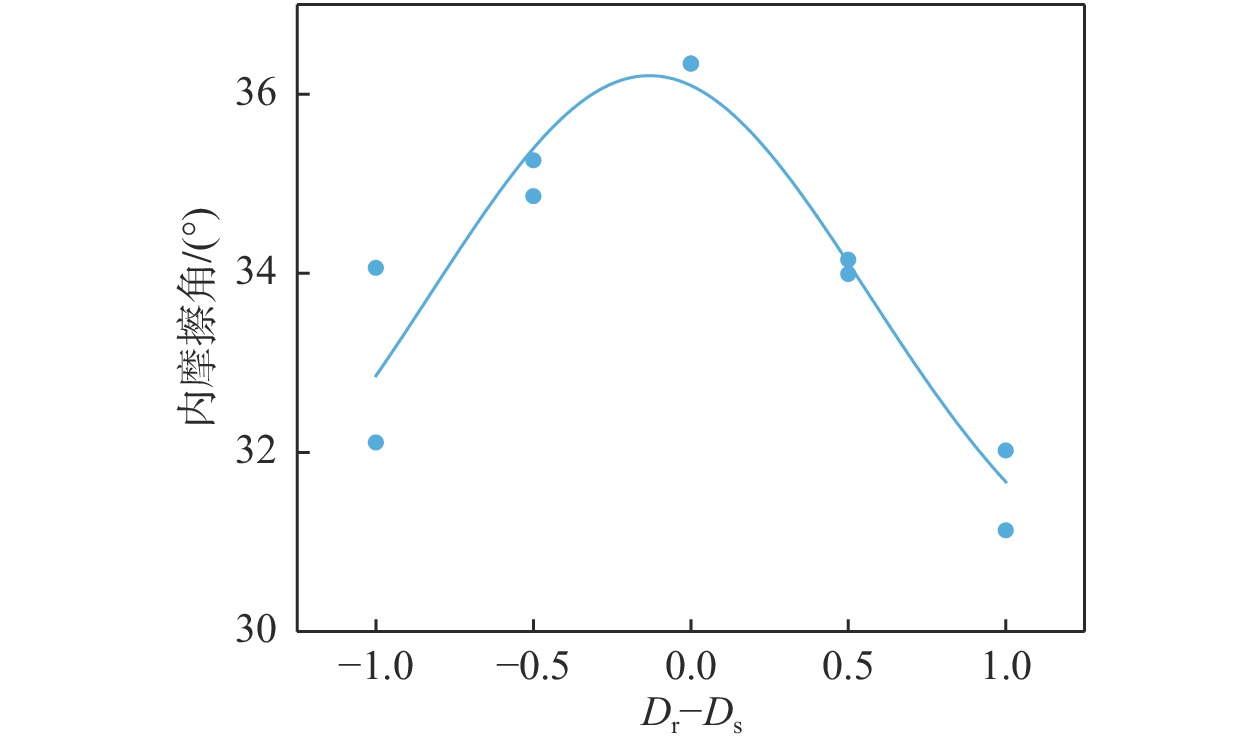
砾石粒度分维值 100 kPa 200 kPa 300 kPa 内摩擦角/(°) 2.45 68.57 144.84 196.07 34.06 2.50 65.22 147.33 209.97 35.26 2.55 69.56 150.10 220.05 36.34 2.60 65.22 123.23 210.78 33.99 2.65 64.84 112.112 195.48 32.02 表 3 不同砂粒度分维值在直剪试验中获取的相关参数
Table 3. Relevant parameters obtained in the direct shear test of the fractal dimension of different sand particle sizes
砂粒度分维值 100 kPa 200 kPa 300 kPa 内摩擦角/(°) 2.45 65.22 143.75 175.31 32.11 2.50 66.09 150.45 202.75 34.86 2.55 69.57 150.10 220.05 36.34 2.60 68.70 135.24 203.53 34.15 2.65 64.44 134.01 170.99 31.13 表 4 不同轴向系数在直剪试验中获取的强度参数
Table 4. Strength parameters obtained in direct shear test with different axial coefficients
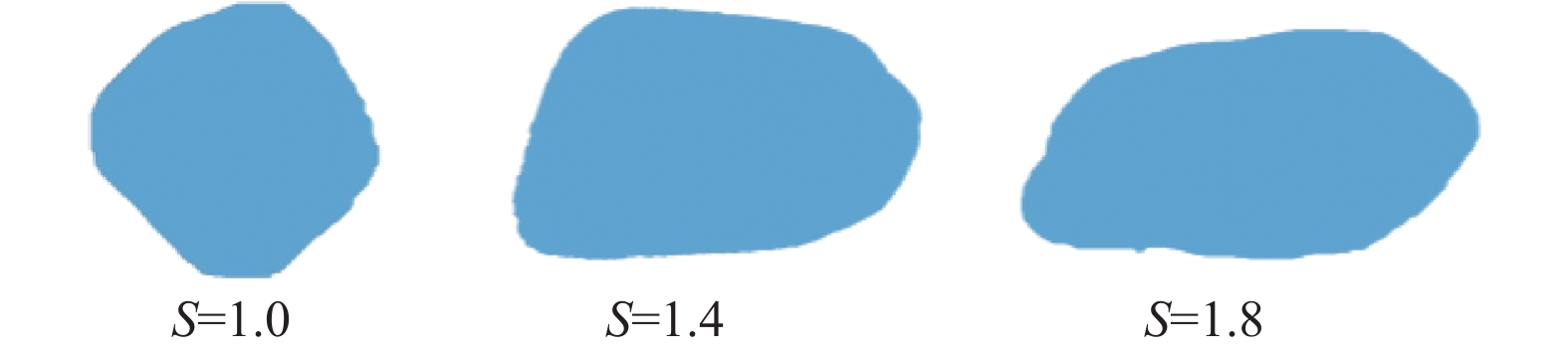
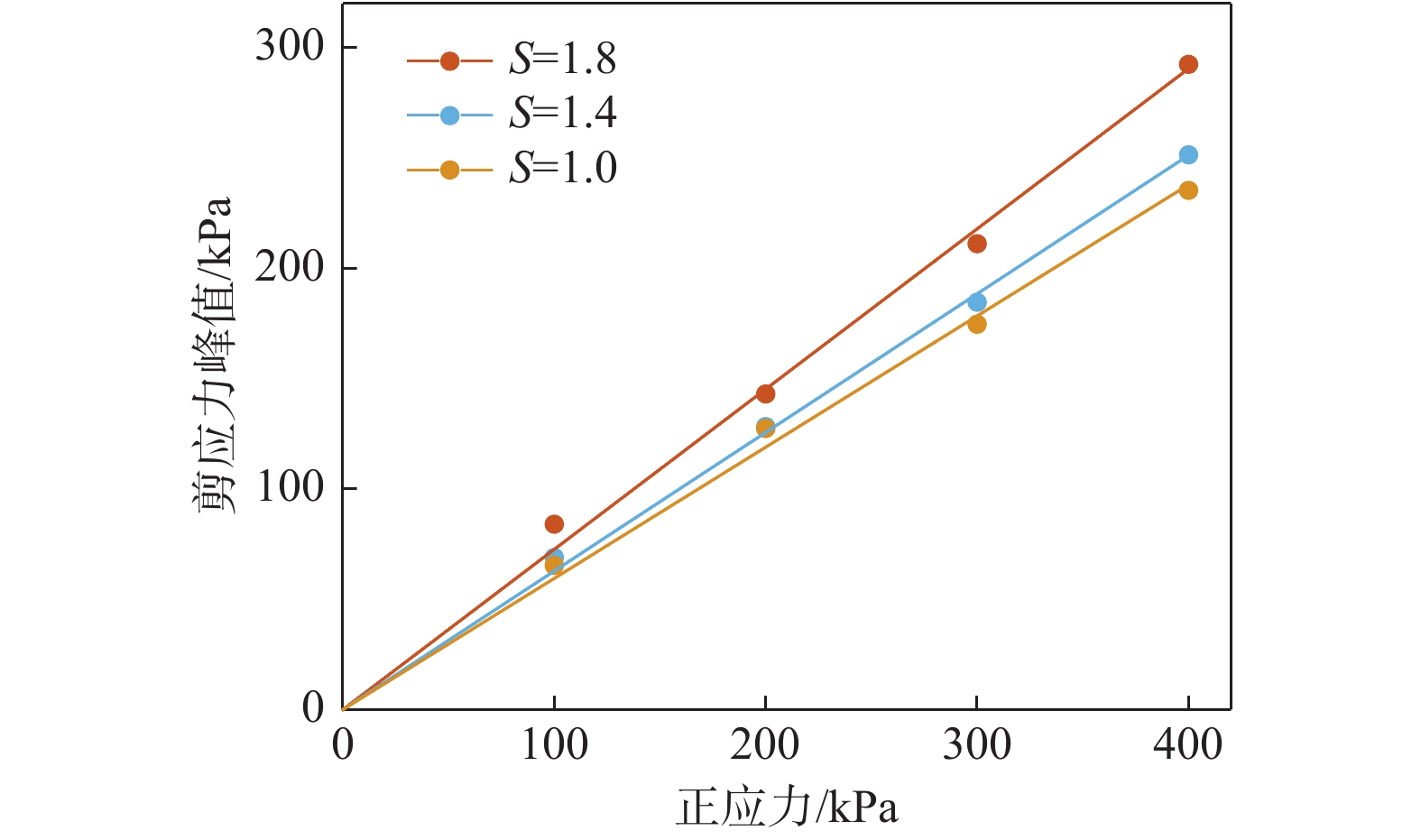
主要参数 轴向系数 S=1.0 S =1.4 S =1.8 100 kPa 65.31 68.91 83.95 200 kPa 127.39 128.25 143.04 300 kPa 174.61 184.58 211.15 400 kPa 235.34 251.42 292.50 内摩擦角/(°) 30.76 32.14 35.92 相关系数R2 0.9919 0.9968 0.9925 表 5 不同轴向系数下砾石接触数量和旋转角度
Table 5. Gravel contact number and rotation angle under different axial coefficients
轴向系数 砾石接触数量 砾石平均旋转角度/(°) 1.0 1581 9.43 1.4 1656 8.70 1.8 1742 6.42 -
[1] 柴贺军, 陈谦应, 孔祥臣, 等. 土石混填路基修筑技术研究综述[J]. 岩土力学,2004,25(6):1005 − 1010. [CHAI Hejun, CHEN Qianying, KONG Xiangchen, et al. Overview of soil-stone high embankment construction study[J]. Rock and Soil Mechanics,2004,25(6):1005 − 1010. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2004.06.037
[2] 廖秋林, 李晓, 郝钊, 等. 土石混合体的研究现状及研究展望[J]. 工程地质学报,2006,14(6):800 − 807. [LIAO Qiulin, LI Xiao, HAO Zhao, et al. Current status and future trends of studies on rock and soil aggregates (RSA)[J]. Journal of Engineering Geology,2006,14(6):800 − 807. (in Chinese with English abstract) doi: 10.3969/j.issn.1004-9665.2006.06.014
[3] 马昊, 黄达, 肖衡林, 等. 江北机场高填方夯后碎块石土剪切力学性质研究[J]. 水文地质工程地质,2019,46(3):88 − 94. [MA Hao, HUANG Da, XIAO Henglin, et al. A study of the shear mechanical properties of high-filled gravel-block soil after dynamic compaction near the Jiangbei airport[J]. Hydrogeology & Engineering Geology,2019,46(3):88 − 94. (in Chinese with English abstract)
[4] 徐文杰, 胡瑞林, 岳中琦, 等. 土石混合体细观结构及力学特性数值模拟研究[J]. 岩石力学与工程学报,2007,26(2):300 − 311. [XU Wenjie, HU Ruilin, YUE Zhongqi, et al. Mesostructural character and numerical simulation of mechanical properties of soil-rock mixtures[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(2):300 − 311. (in Chinese with English abstract) doi: 10.3321/j.issn:1000-6915.2007.02.011
[5] 廖秋林, 李晓, 朱万成, 等. 基于数码图像土石混合体结构建模及其力学结构效应的数值分析[J]. 岩石力学与工程学报,2010,29(1):155 − 162. [LIAO Qiulin, LI Xiao, ZHU Wancheng, et al. Structure model construction of rock and soil aggregate based on digital image technology and its numerical simulation on mechanical structure effects[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(1):155 − 162. (in Chinese with English abstract)
[6] 赵鑫曜, 陈建功, 张海权, 等. 基于块石形状数据库的土石混合体模型随机生成方法[J]. 岩土力学,2018,39(12):4691 − 4697. [ZHAO Xinyao, CHEN Jiangong, ZHANG Haiquan, et al. Random generation of soil-rock mixture models by rock shape database using digital imaging technology[J]. Rock and Soil Mechanics,2018,39(12):4691 − 4697. (in Chinese with English abstract)
[7] 袁斌, 霍宇翔, 巨能攀, 等. 颗粒棱度指标的改进及其对剪切特性的影响[J]. 水文地质工程地质,2020,47(4):167 − 173. [YUAN Bin, HUO Yuxiang, JU Nengpan, et al. Improvement of grain edge index and its effect on shear characteristics[J]. Hydrogeology & Engineering Geology,2020,47(4):167 − 173. (in Chinese with English abstract)
[8] 杜修力, 张佩, 金浏, 等. 基于分形理论的北京地区砂砾石地层细观建模[J]. 岩石力学与工程学报,2017,36(2):437 − 445. [DU Xiuli, ZHANG Pei, JIN Liu, et al. A mesoscopic model of sand-gravel stratum in Beijing based on fractal theory[J]. Chinese Journal of Rock Mechanics and Engineering,2017,36(2):437 − 445. (in Chinese with English abstract)
[9] 舒志乐, 刘新荣, 刘保县, 等. 土石混合体粒度分形特性及其与含石量和强度的关系[J]. 中南大学学报(自然科学版),2010,41(3):1096 − 1101. [SHU Zhile, LIU Xinrong, LIU Baoxian, et al. Granule fractal properties of earth-rock aggregate and relationship between its gravel content and strength[J]. Journal of Central South University (Science and Technology),2010,41(3):1096 − 1101. (in Chinese with English abstract)
[10] 汪海年, 郝培文. 粗集料二维形状特征的图像描述[J]. 建筑材料学报,2009,12(6):747 − 751. [WANG Hainian, HAO Peiwen. Digital description of two-dimensional shape characteristics of coarse aggregate[J]. Journal of Building Materials,2009,12(6):747 − 751. (in Chinese with English abstract) doi: 10.3969/j.issn.1007-9629.2009.06.025
[11] TYLER S W, WHEATCRAFT S W. Fractal scaling of soil particle-size distributions: analysis and limitations[J]. Soil Science Society of America Journal,1992,56(2):362 − 369. doi: 10.2136/sssaj1992.03615995005600020005x
[12] 王江营, 曹文贵, 张超, 等. 基于正交设计的复杂环境下土石混填体大型直剪试验研究[J]. 岩土工程学报,2013,35(10):1849 − 1856. [WANG Jiangying, CAO Wengui, ZHANG Chao, et al. Large-scale direct shear tests on soil-rock aggregate mixture under complicated environment based on orthogonal design[J]. Chinese Journal of Geotechnical Engineering,2013,35(10):1849 − 1856. (in Chinese with English abstract)
[13] 董云. 土石混合料强度特性的试验研究[J]. 岩土力学,2007,28(6):1269 − 1274. [DONG Yun. Experimental study on intensity character of rock-soil aggregate mixture[J]. Rock and Soil Mechanics,2007,28(6):1269 − 1274. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2007.06.040
[14] 徐文杰, 胡瑞林, 岳中崎. 土–石混合体随机细观结构生成系统的研发及其细观结构力学数值试验研究[J]. 岩石力学与工程学报,2009,28(8):1652 − 1665. [XU Wenjie, HU Ruilin, YUE Zhongqi. Development of random mesostructure generating system of soil-rock mixture and study of its mesostructural mechanics based on numerical test[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1652 − 1665. (in Chinese with English abstract) doi: 10.3321/j.issn:1000-6915.2009.08.017
[15] 徐文杰, 胡瑞林. 土石混合体概念、分类及意义[J]. 水文地质工程地质,2009,36(4):50 − 56. [XU Wenjie, HU Ruilin. Conception, classification and significations of soil-rock mixture[J]. Hydrogeology & Engineering Geology,2009,36(4):50 − 56. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-3665.2009.04.012
[16] 赵金凤, 严颖, 季顺迎. 基于离散元模型的土石混合体直剪试验分析[J]. 固体力学学报,2014,35(2):124 − 134. [ZHAO Jinfeng, YAN Ying, JI Shunying. Analysis of direct shear test of soil-rock mixture based on discrete element model[J]. Chinese Journal of Solid Mechanics,2014,35(2):124 − 134. (in Chinese with English abstract)
[17] 张昭, 魏星, 王刚. 颗粒长短轴比对饱和砂土液化影响的离散元分析[J]. 路基工程,2018(5):40 − 44. [ZHANG Zhao, WEI Xing, WANG Gang. DEM study on effect of particle long-short-axes ratio on liquefaction of saturated sand[J]. Subgrade Engineering,2018(5):40 − 44. (in Chinese with English abstract)
-



 下载:
下载: