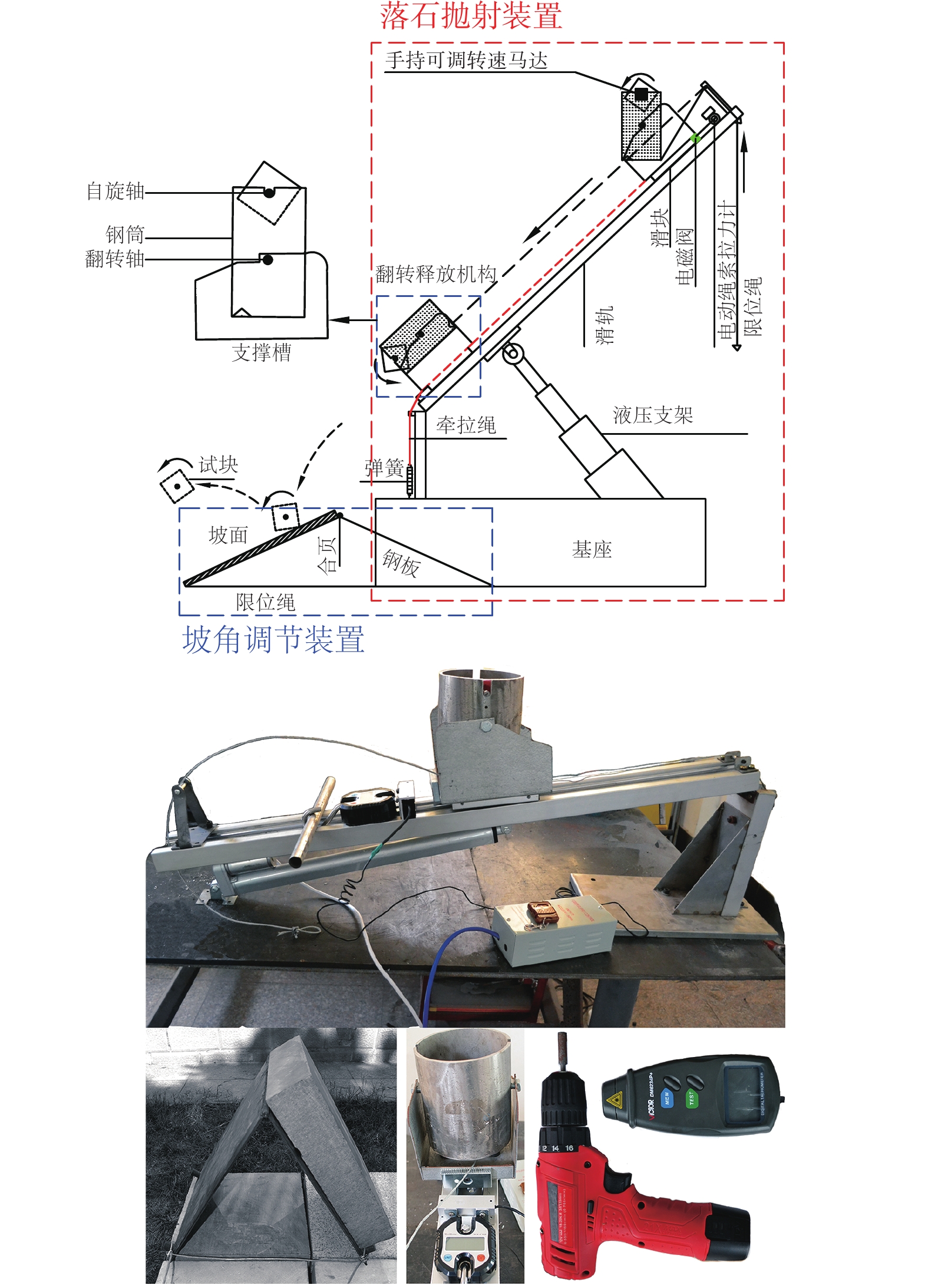
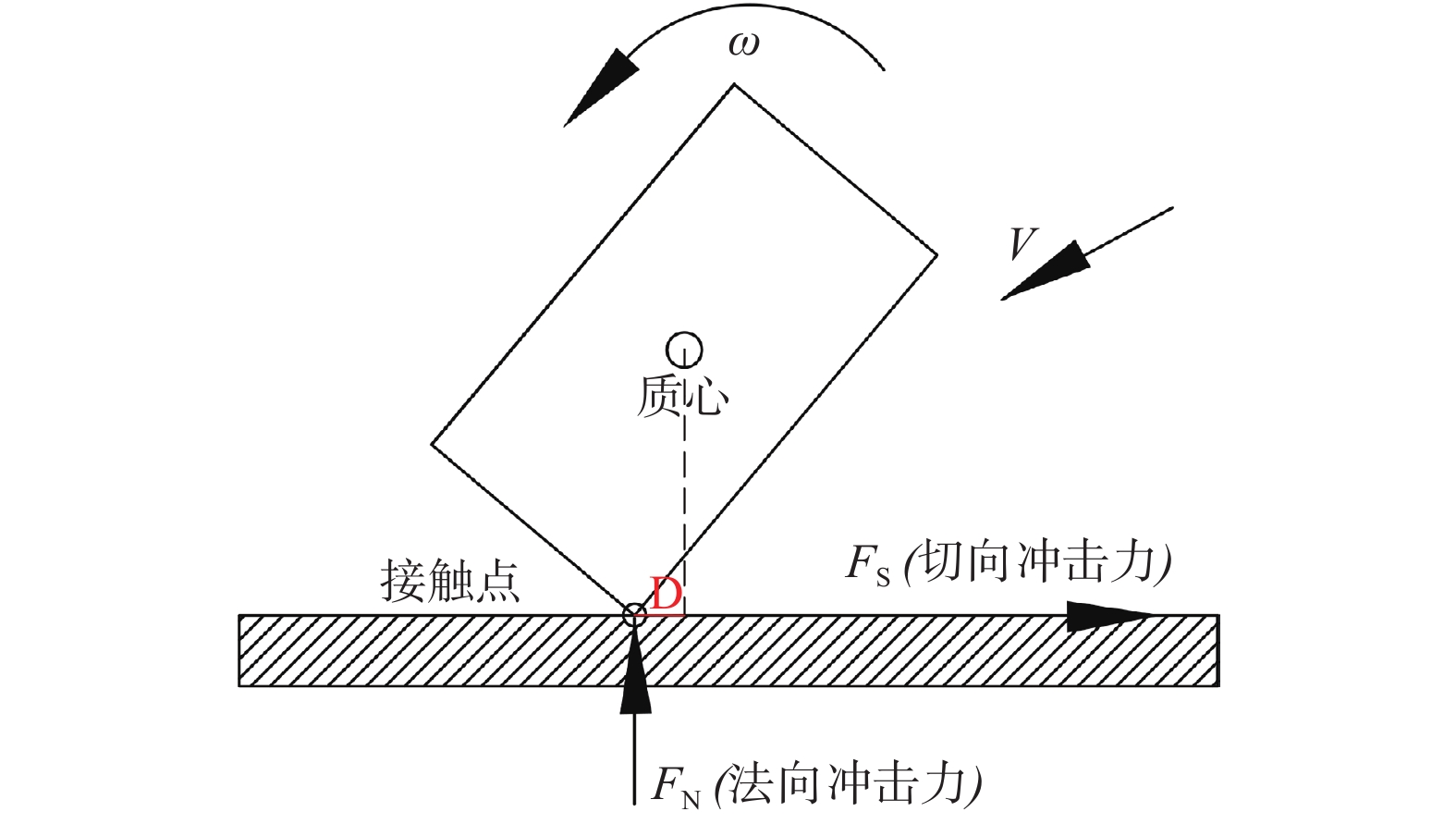
Research on the joint influence of multiple factors on the normal coefficient of restitution of rockfall
-
摘要:
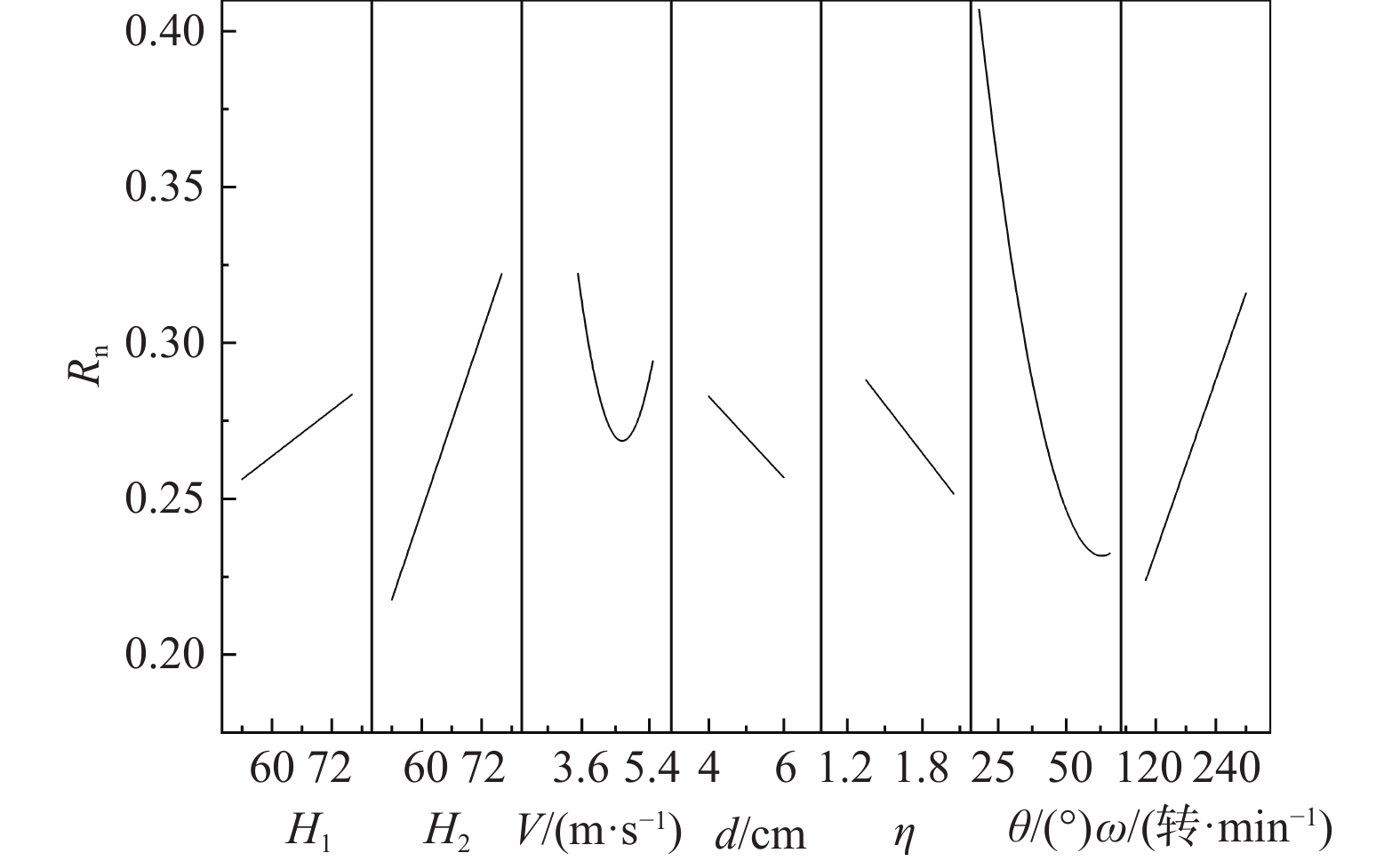
法向恢复系数(Rn)作为落石灾害预测及分析中最为关键的输入参数,由于其受控因素较多,如何确定准确合理的Rn值仍然是一个难题。为探究多因素对Rn的联合影响规律及机理,首次采用响应曲面−中心复合试验设计方法对Rn的7因素联合影响展开测试。通过对试验结果进行回归和方差分析,遴选的7个因素对Rn影响均较显著,显著程度依次为碰撞角(θ)>试块硬度(H1)>转速(ω)>形状因子(η)>入射速度(V)>坡面硬度(H2)>尺寸(d)。许多交互参数对Rn亦表现出了显著影响,依次为d−θ > H1−d > V−η > H1−ω > d−η > η−ω > H1−η。对于单因素参数,Rn随d、V、η、θ减小和H1、H2、ω增大,呈增大趋势;对于交互参数,d和ω对Rn影响较弱仅表现在H1较小时,随H1增大,影响逐渐增强;η在H1较小时对Rn影响较显著,随H1增大,影响明显减弱;η较小时,Rn随V或d减小显著增大,η较大时,这种影响不显著;θ较小时,Rn随θ增大减小较快,θ较大时,减小趋势放缓;相比较小η值试块,较大η值试块的ω对Rn影响更为显著。这些获得的结论可为落石Rn计算模型的构建提供重要参考,进而为落石灾害的精准预测及防护提供依据。
Abstract:The normal coefficient of restitution (Rn) is the most critical input parameter in the prediction and analysis of rockfall disasters. Because of its many controlling factors, how to determine an accurate and reasonable value of Rn is still a difficult problem. In order to explore the law and mechanism of the joint influence of multiple factors on Rn, the response surface methodology-central composite design method is used to investigate the combined effect of seven factors on Rn for the first time. Through regression and variance analysis of the test results, the seven selected factors have the significant effects on Rn, and the order of significance is the impact angle (θ) > block hardness (H1) > rotational speed (ω) > shape factor (η) > incident velocity (V) > slope hardness (H2) > size (d). Many interaction parameters also show the significant effects on Rn, in the order of d−θ > H1−d > V−η > H1−ω > d−η > η−ω > H1−η. For a single factor parameter, Rn increases with the decrease of d, V, η, θ and the increase of H1, H2, ω; for interaction parameters, d and ω have a weak effect on Rn, only when H1 is small, and the effect gradually increases with the increase of H1; η has a significant effect on Rn when H1 is small, and the effect significantly decreases with the increase of H1; when η is small, Rn increases significantly with the decrease of V or d, and this effect is not significant when η is large; when θ is small, Rn decreases rapidly with the increase of θ, and the decreasing trend slows down when θ is large. Compared with block with small η, the ω of block with larger η has a more significant effect on Rn. These conclusions can provide an important reference for the construction of the Rn calculation model of rockfall, and provide a basis for the accurate prediction and prevention of rockfall disasters.
-
Key words:
- rockfall /
- normal coefficient of restitution /
- response surface /
- joint influence /
- interactive effect
-

-
表 1 中心复合试验设计中的变量水平
Table 1. Variable levels in the central composite experimental design
编码因子变量 实际因子变量 实际水平 低轴点 低水平 中心点 高水平 高轴点 −α (−1.576) −1 0 1 +α (+1.576) A 坡面硬度(H2) 47.66 54 65 76 82.33 B 试块硬度(H1) 47.66 54 65 76 82.33 C 入射速度(V)/(m· s−1) 2.92 3.5 4.5 5.5 6.08 D 尺寸/等效直径(d)/cm 3.42 4 5 6 6.58 E 形状因子(η) 1.15 1.35 1.70 2.05 2.25 F 碰撞角(θ)/(°) 4.18 18 42 66 79.82 G 初始转速(ω)/(转·min−1) 42 100 200 300 358 表 2 试验所用试块及坡面板特征参数
Table 2. Characteristic parameters of the blocks and slopes used in the experiment
岩石类型 施密特硬度 形状 尺寸 η 特征长度 值/mm 大理岩 54 长方体 长/宽/高 53.9/24.9/24.9 2.05 大理岩 54 长方体 长/宽/高 80.85/37.35/37.35 2.05 大理岩 54 近似立方体 长/宽/高 52.58/46.35/46.35 1.35 大理岩 54 近似立方体 长/宽/高 35.05/30.9/30.9 1.35 花岗岩-1 76 长方体 长/宽/高 53.9/24.9/24.9 2.05 花岗岩-1 76 长方体 长/宽/高 80.85/37.35/37.35 2.05 花岗岩-1 76 近似立方体 长/宽/高 52.58/46.35/46.35 1.35 花岗岩-1 76 近似立方体 长/宽/高 35.05/30.9/30.9 1.35 灰岩 65 正四面体 边长 82 1.70 灰岩 65 正四面体 边长 56.28 1.70 灰岩 65 正四面体 边长 108.06 1.70 灰岩 65 正二十面体 边长 31.07 1.15 灰岩 65 三角板 底边/高/厚度 57.1/70.6/32.65 2.25 花岗岩-2 82 正四面体 边长 82 1.70 砂岩 48 正四面体 边长 82 1.70 表 3 Rn值的响应曲面二次模型方差分析结果
Table 3. Analyses of variance (ANOVA) for the response surface quadratic model of the Rn values
方差来源 SS df MS F值 P值
Prob > F模型
系数截距 0.27 A 0.025 1 0.025 21.18 < 0.0001 0.014 B 0.36 1 0.36 313.27 < 0.0001 0.052 C 0.026 1 0.026 22.55 < 0.0001 −0.014 D 0.023 1 0.023 19.39 < 0.0001 −0.013 E 0.044 1 0.044 37.9 < 0.0001 −0.018 F 1.01 1 1.01 871.14 < 0.0001 −0.087 G 0.28 1 0.28 242.17 < 0.0001 0.046 BD 0.0099 1 0.0099 8.51 0.0042 0.0088 BE 0.0046 1 0.0046 3.96 0.0486 0.006 BF 0.0034 1 0.0034 2.91 0.0902 −0.0051 BG 0.0068 1 0.0068 5.84 0.017 0.0073 CE 0.0086 1 0.0086 7.36 0.0076 0.0082 DE 0.0062 1 0.0062 5.3 0.0228 0.0069 DF 0.012 1 0.012 9.93 0.002 0.0095 DG 0.0024 1 0.0024 2.11 0.1491 0.0044 EF 0.0026 1 0.0026 2.27 0.1347 0.0045 EG 0.0049 1 0.0049 4.23 0.0418 0.0062 C2 0.027 1 0.027 23.29 < 0.0001 0.038 F2 0.046 1 0.046 39.29 < 0.0001 0.05 Model 1.98 19 0.1 89.5 < 0.0001 Lack of Fit 0.14 123 0.0012 0.99 0.5649 R2=0.928 -
[1] 何思明, 吴永, 李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学,2009,30(3):623 − 627. [HE Siming, WU Yong, LI Xinpo. Research on restitution coefficient of rock fall[J]. Rock and Soil Mechanics,2009,30(3):623 − 627. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2009.03.008
[2] 章广成, 向欣, 唐辉明. 落石碰撞恢复系数的现场试验与数值计算[J]. 岩石力学与工程学报,2011,30(6):1266 − 1273. [ZHANG Guangcheng, XIANG Xin, TANG Huiming. Field test and numerical calculation of restitution coefficient of rockfall collision[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(6):1266 − 1273. (in Chinese with English abstract)
[3] 姬中民, 唐一举, 伍法权, 等. 落石形状和尺寸对恢复系数影响的室内试验研究[J]. 岩土力学,2021,42(3):665 − 672. [JI Zhongmin, TANG Yiju, WU Faquan, et al. Laboratory investigation of the effect of rockfall shape and size on coefficient of restitution[J]. Rock and Soil Mechanics,2021,42(3):665 − 672. (in Chinese with English abstract)
[4] 吴建利, 胡卸文, 梅雪峰, 等. 落石冲击混凝土板与缓冲层组合结构的动力响应[J]. 水文地质工程地质,2021,48(1):78 − 87. [WU Jianli, HU Xiewen, MEI Xuefeng, et al. Dynamic response of RC slab with cushion layer composed of sandy soil to rockfall impact[J]. Hydrogeology & Engineering Geology,2021,48(1):78 − 87. (in Chinese with English abstract)
[5] 吴建利, 胡卸文, 梅雪峰, 等. 高位落石作用下不同缓冲层与钢筋混凝土板组合结构动力响应[J]. 水文地质工程地质,2020,47(4):114 − 122. [WU Jianli, HU Xiewen, MEI Xuefeng, et al. Dynamic response of RC plate with different cushion layers under the high-level rockfall impact[J]. Hydrogeology & Engineering Geology,2020,47(4):114 − 122. (in Chinese with English abstract)
[6] 沈均, 何思明, 吴永. 滚石灾害研究现状及发展趋势[J]. 灾害学,2008,23(4):122 − 125. [SHEN Jun, HE Siming, WU Yong. Present research status and development trend of rockfall hazards[J]. Journal of Catastrophology,2008,23(4):122 − 125. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-811X.2008.04.025
[7] YAN P, ZHANG J H, KONG X Z, et al. Numerical simulation of rockfall trajectory with consideration of arbitrary shapes of falling rocks and terrain[J]. Computers and Geotechnics,2020,122:103511. doi: 10.1016/j.compgeo.2020.103511
[8] AGLIARDI F, CROSTA G B. High resolution three-dimensional numerical modelling of rockfalls[J]. International Journal of Rock Mechanics and Mining Sciences,2003,40(4):455 − 471. doi: 10.1016/S1365-1609(03)00021-2
[9] LAN H X, MARTIN C D, LIM C H. RockFall analyst: a GIS extension for three dimensional and spatially distributed rockfall hazard modeling[J]. Computers & Geosciences,2007,33(2):262 − 279.
[10] STEVENS W. RockFall: a tool for probabilistic analysis, design of remedial measures and prediction of rock falls[D].Toronto: University of Toronto, 1998.
[11] DORREN L K A. Rockyfor3D (v5.2) revealed-transparent description of the complete 3D rockfall model[EB/OL]. (2015-12-16)[2021-04-20]. http://www.ecorisq.org/
[12] LI L P, LAN H X. Probabilistic modeling of rockfall trajectories: a review[J]. Bulletin of Engineering Geology and the Environment,2015,74(4):1163 − 1176. doi: 10.1007/s10064-015-0718-9
[13] 叶四桥, 巩尚卿. 落石碰撞法向恢复系数的模型试验研究[J]. 中国铁道科学,2015,36(4):13 − 19. [YE Siqiao, GONG Shangqing. Research on normal restitution coefficient of rockfall collision by model tests[J]. China Railway Science,2015,36(4):13 − 19. (in Chinese with English abstract) doi: 10.3969/j.issn.1001-4632.2015.04.03
[14] 黄润秋, 刘卫华. 基于正交设计的滚石运动特征现场试验研究[J]. 岩石力学与工程学报,2009,28(5):882 − 891. [HUANG Runqiu, LIU Weihua. In-situ test study of characteristics of rolling rock blocks based on orthogonal design[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(5):882 − 891. (in Chinese with English abstract) doi: 10.3321/j.issn:1000-6915.2009.05.003
[15] 叶四桥, 巩尚卿, 王林峰, 等. 落石碰撞切向恢复系数的取值研究[J]. 中国铁道科学,2018,39(1):8 − 15. [YE Siqiao, GONG Shangqing, WANG Linfeng, et al. Research on value of tangential restitution coefficient for rockfall collision[J]. China Railway Science,2018,39(1):8 − 15. (in Chinese with English abstract) doi: 10.3969/j.issn.1001-4632.2018.01.02
[16] GIANI G P, GIACOMINI A, MIGLIAZZA M, et al. Experimental and theoretical studies to improve rock fall analysis and protection work design[J]. Rock Mechanics and Rock Engineering,2004,37(5):369 − 389. doi: 10.1007/s00603-004-0027-2
[17] SPADARI M, GIACOMINI A, BUZZI O, et al. In situ rockfall testing in New South Wales, Australia[J]. International Journal of Rock Mechanics and Mining Sciences,2012,49:84 − 93. doi: 10.1016/j.ijrmms.2011.11.013
[18] FERRARI F, GIANI G P, APUANI T. Why can rockfall normal restitution coefficient be higher than one?[J]. Rend Online Soc Geol It, 2013, 24: 122 − 124.
[19] WYLLIE D C. Calibration of rock fall modeling parameters[J]. International Journal of Rock Mechanics and Mining Sciences,2014,67:170 − 180. doi: 10.1016/j.ijrmms.2013.10.002
[20] PFEIFFER T, BOWEN T. Computer simulation of rockfalls[J]. Environmental & Engineering Geoscience,1989,26(1):135 − 146.
[21] ASTERIOU P, TSIAMBAOS G. Empirical model for predicting rockfall trajectory direction[J]. Rock Mechanics and Rock Engineering,2016,49(3):927 − 941. doi: 10.1007/s00603-015-0798-7
[22] ASTERIOU P, TSIAMBAOS G. Effect of impact velocity, block mass and hardness on the coefficients of restitution for rockfall analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2018,106:41 − 50. doi: 10.1016/j.ijrmms.2018.04.001
[23] ASTERIOU P, SAROGLOU H, TSIAMBAOS G. Geotechnical and kinematic parameters affecting the coefficients of restitution for rock fall analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2012,54:103 − 113. doi: 10.1016/j.ijrmms.2012.05.029
[24] JI Z M, CHEN Z J, NIU Q H, et al. Laboratory study on the influencing factors and their control for the coefficient of restitution during rockfall impacts[J]. Landslides,2019,16(10):1939 − 1963. doi: 10.1007/s10346-019-01183-x
[25] GIACOMINI A, THOENI K, LAMBERT C, et al. Experimental study on rockfall drapery systems for open pit highwalls[J]. International Journal of Rock Mechanics and Mining Sciences,2012,56:171 − 181. doi: 10.1016/j.ijrmms.2012.07.030
[26] ANSARI M K, AHMAD M, SINGH R, et al. Correlation between Schmidt hardness and coefficient of restitution of rocks[J]. Journal of African Earth Sciences,2015,104:1 − 5. doi: 10.1016/j.jafrearsci.2015.01.005
[27] CHAU K T, WONG R H C, LEE F. Rockfall problems in Hong Kong and some new experimental results for coefficients of restitution[J]. International Journal of Rock Mechanics and Mining Sciences,1998,35(4/5):662 − 663.
[28] TURRIN S, HANSS M, SELVADURAI A P S. An approach to uncertainty analysis of rockfall Simulation[J]. Computer Modeling in Engineering & Sciences,2009,52(3):237 − 258.
[29] BUZZI O, GIACOMINI A, SPADARI M. Laboratory investigation on high values of restitution coefficients[J]. Rock Mechanics and Rock Engineering,2012,45(1):35 − 43.
[30] 柳万里, 晏鄂川, 魏鹏飞, 等. 落石运动特征试验及影响因素敏感性分析[J]. 山地学报,2021,39(1):47 − 58. [LIU Wanli, YAN Echuan, WEI Pengfei, et al. Experimental study on rockfall and sensitivity analysis of influencing factors[J]. Mountain Research,2021,39(1):47 − 58. (in Chinese with English abstract)
[31] SAKKAS V A, ISLAM M A, STALIKAS C, et al. Photocatalytic degradation using design of experiments: A review and example of the Congo red degradation[J]. Journal of Hazardous Materials,2010,175(1/2/3):33 − 44.
[32] FITYUS S G, GIACOMINI A, BUZZI O. The significance of geology for the morphology of potentially unstable rocks[J]. Engineering Geology,2013,162:43 − 52. doi: 10.1016/j.enggeo.2013.05.007
-



 下载:
下载: