A study of numerical simulations for enhanced geothermal reservoir parameters and thermal extraction based on microseismic data
-
摘要:
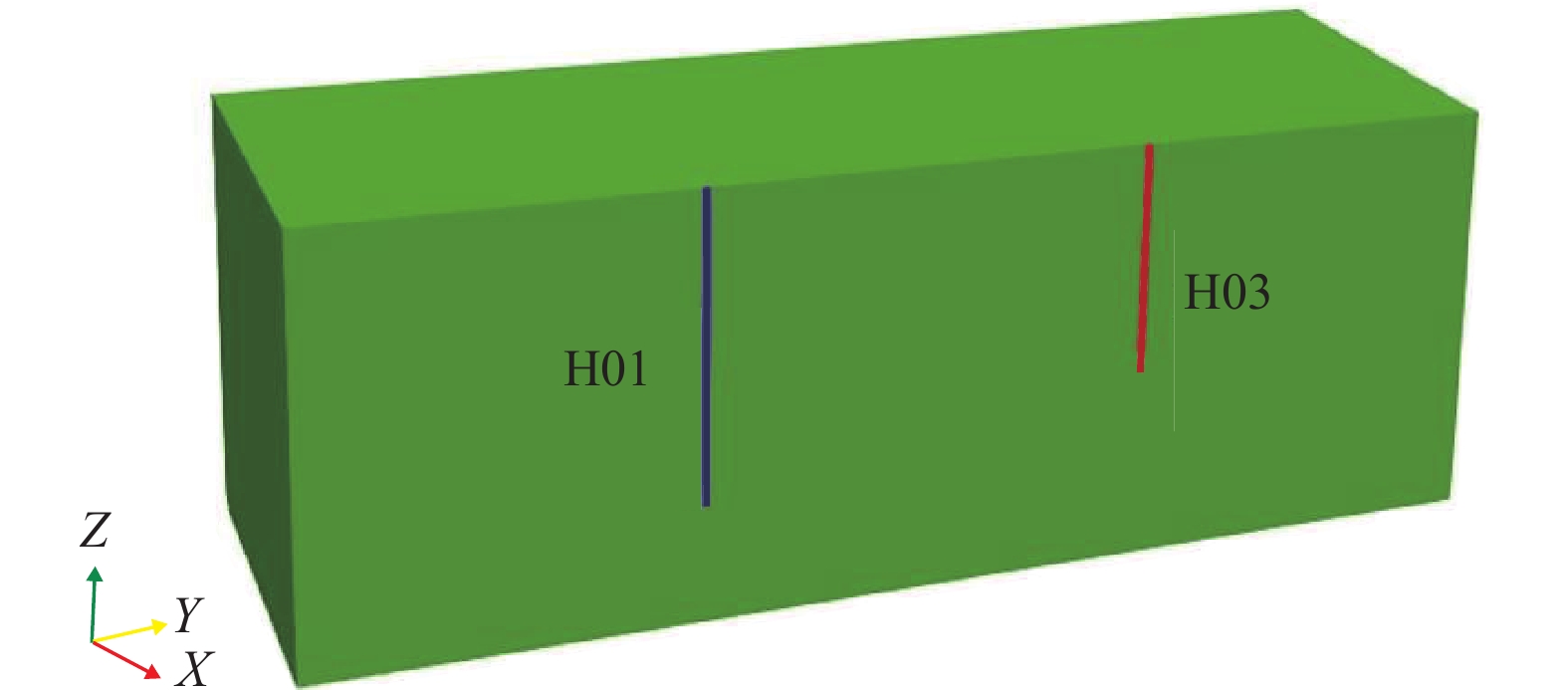
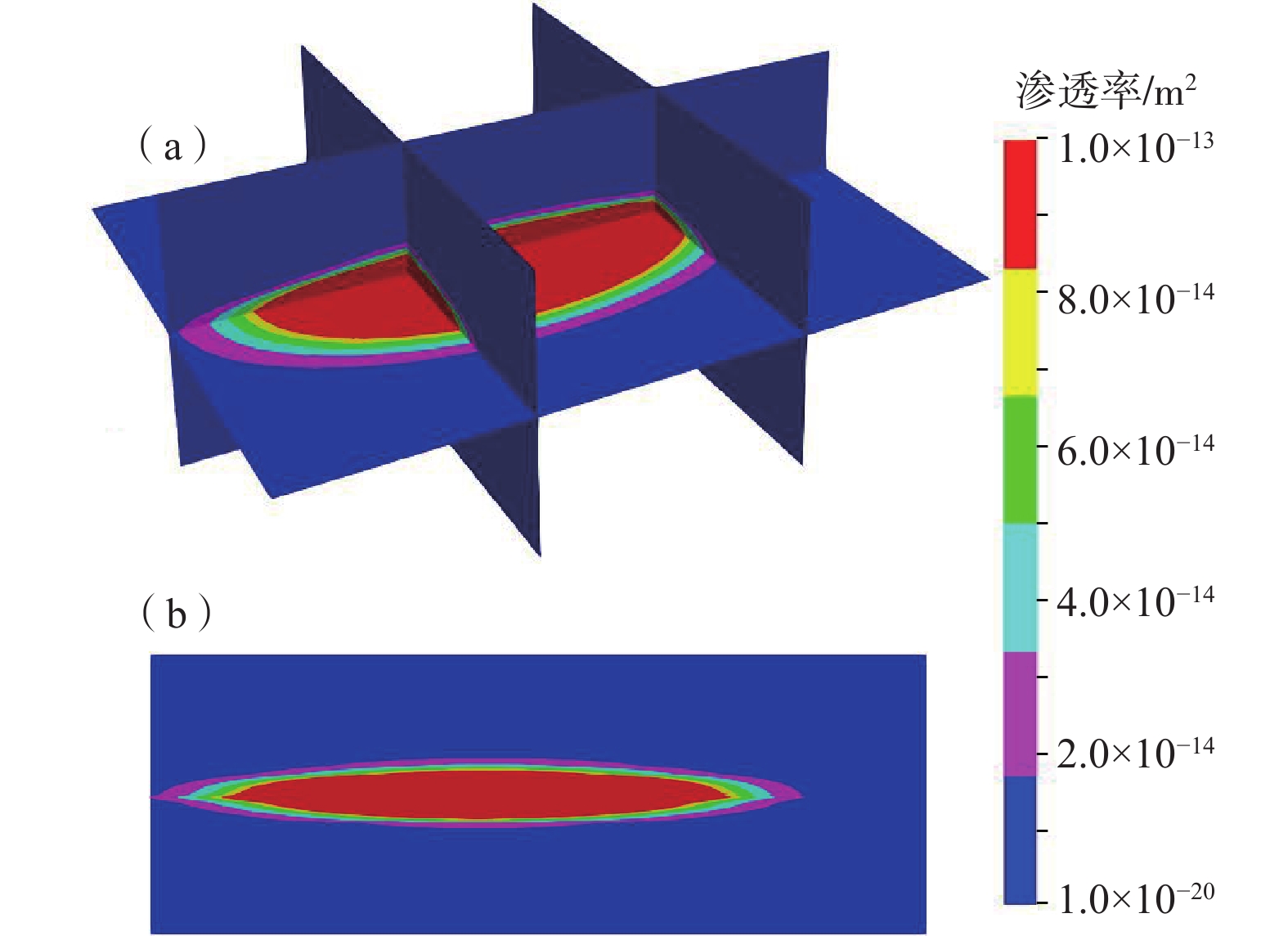
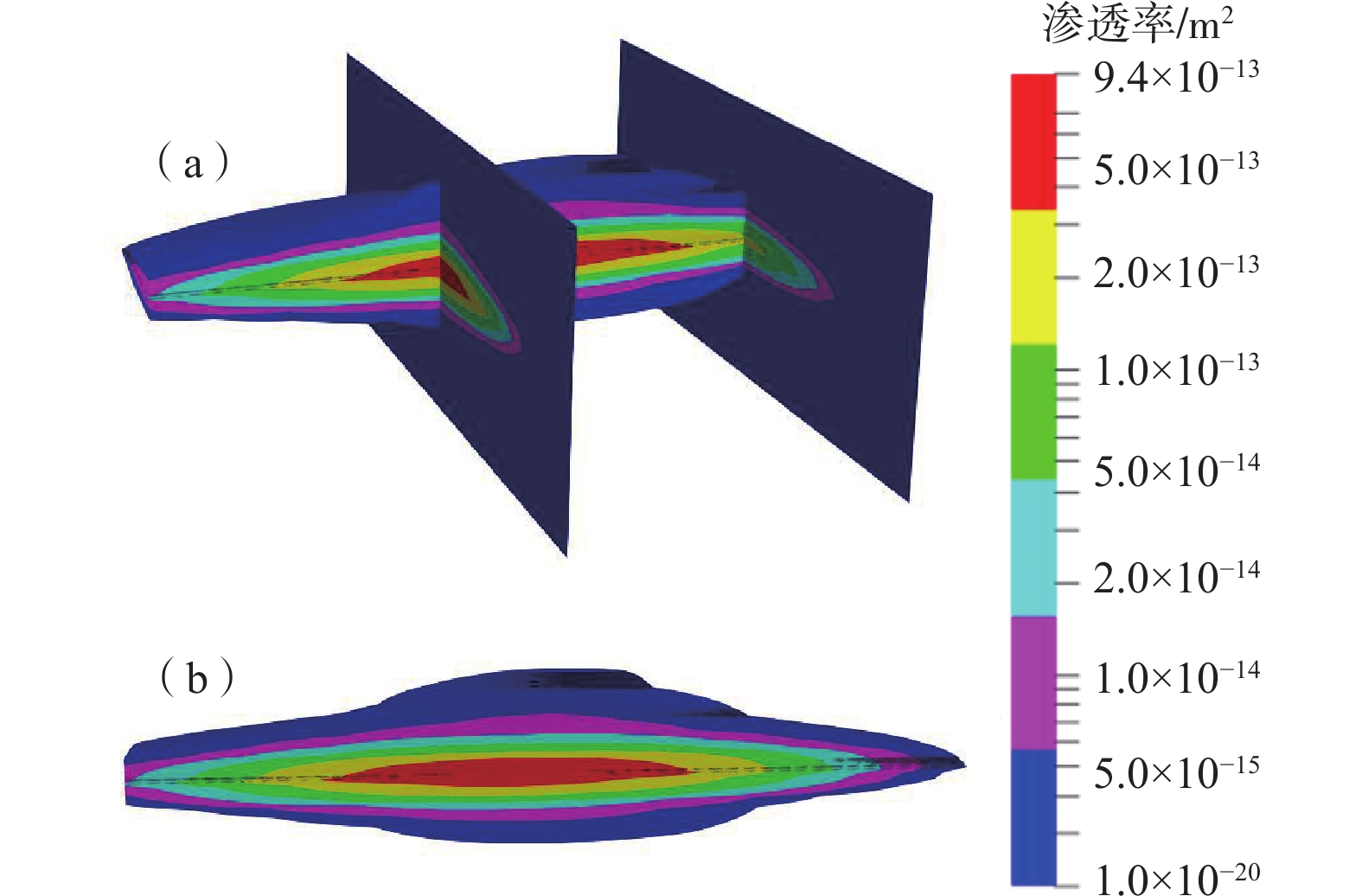
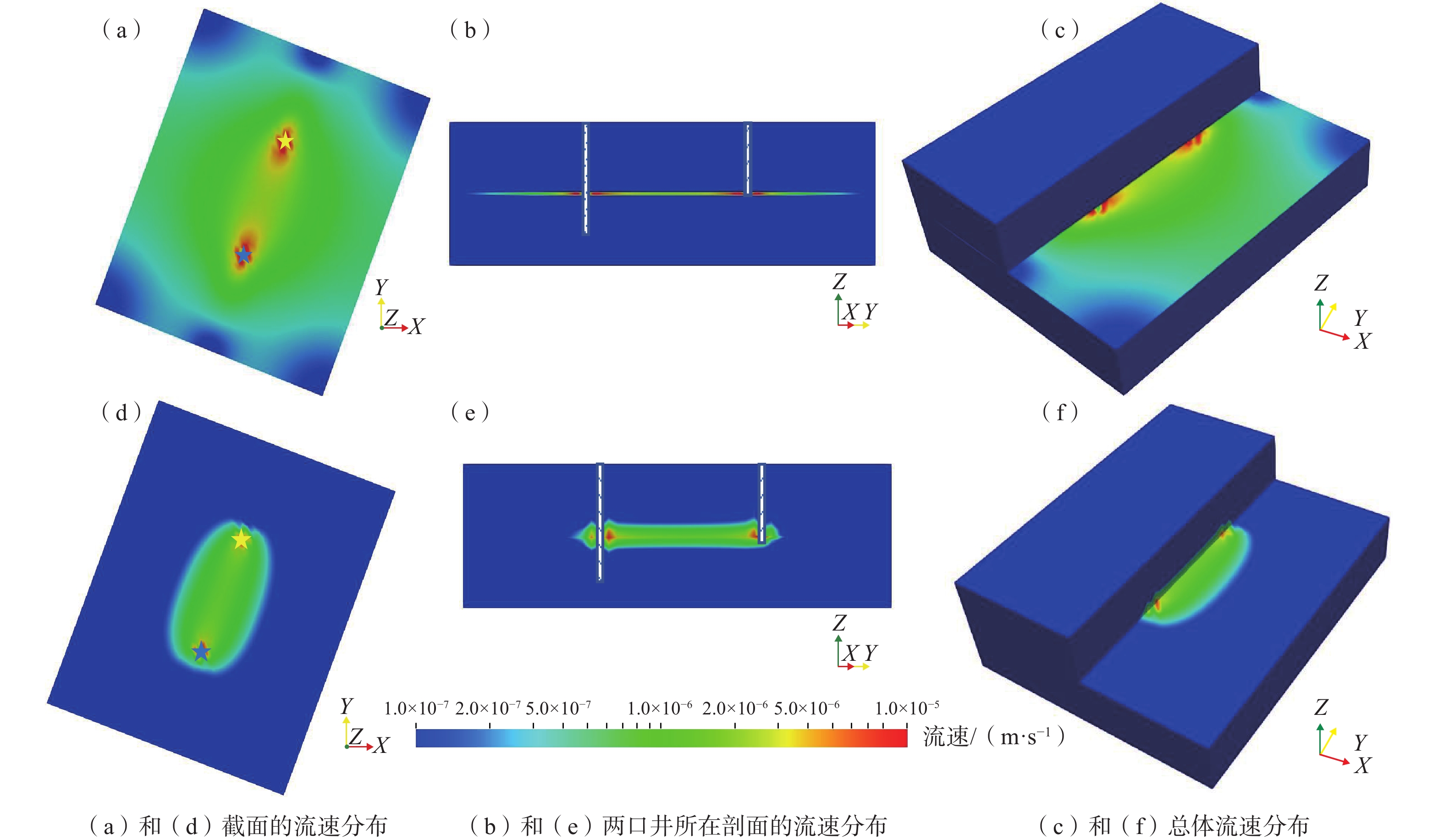
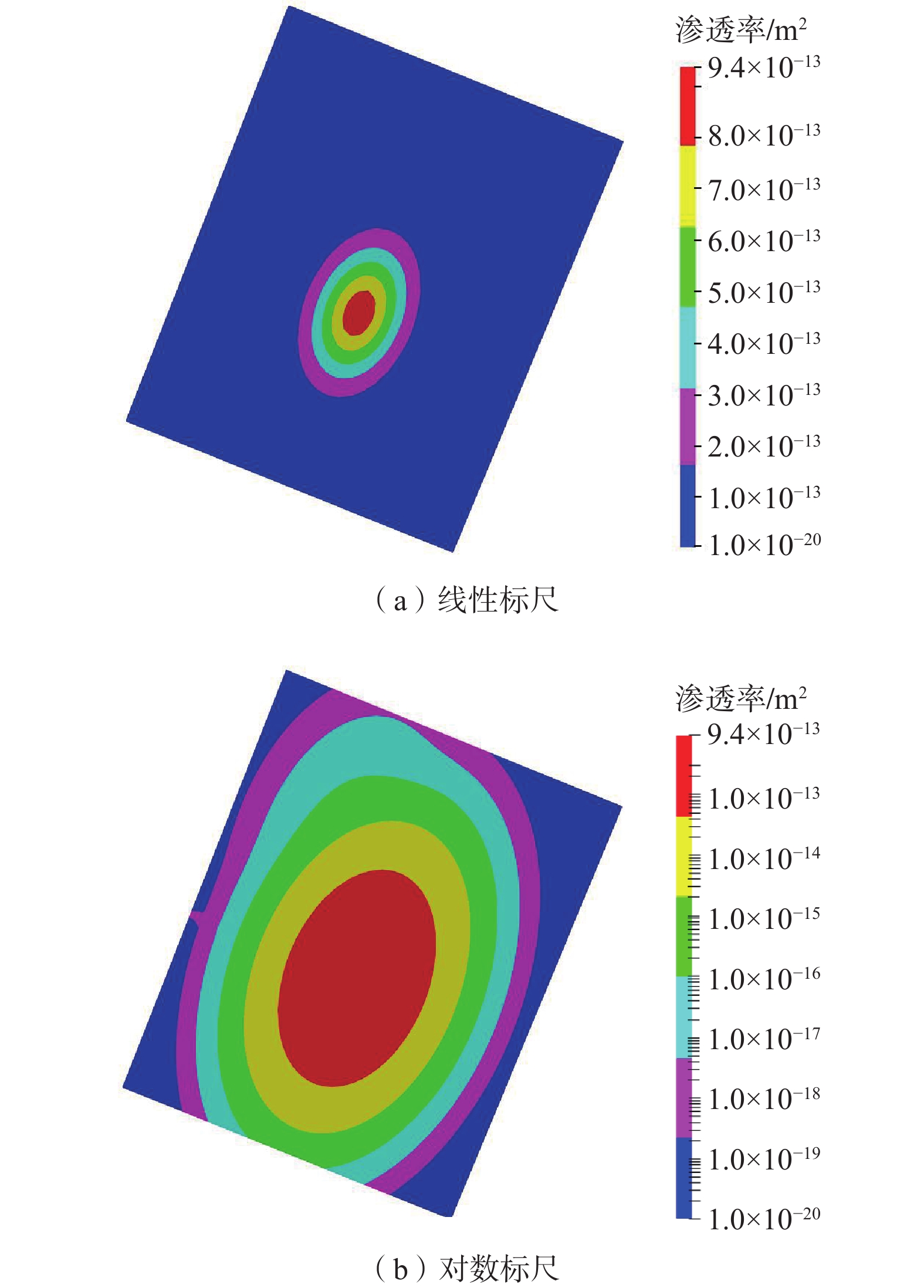
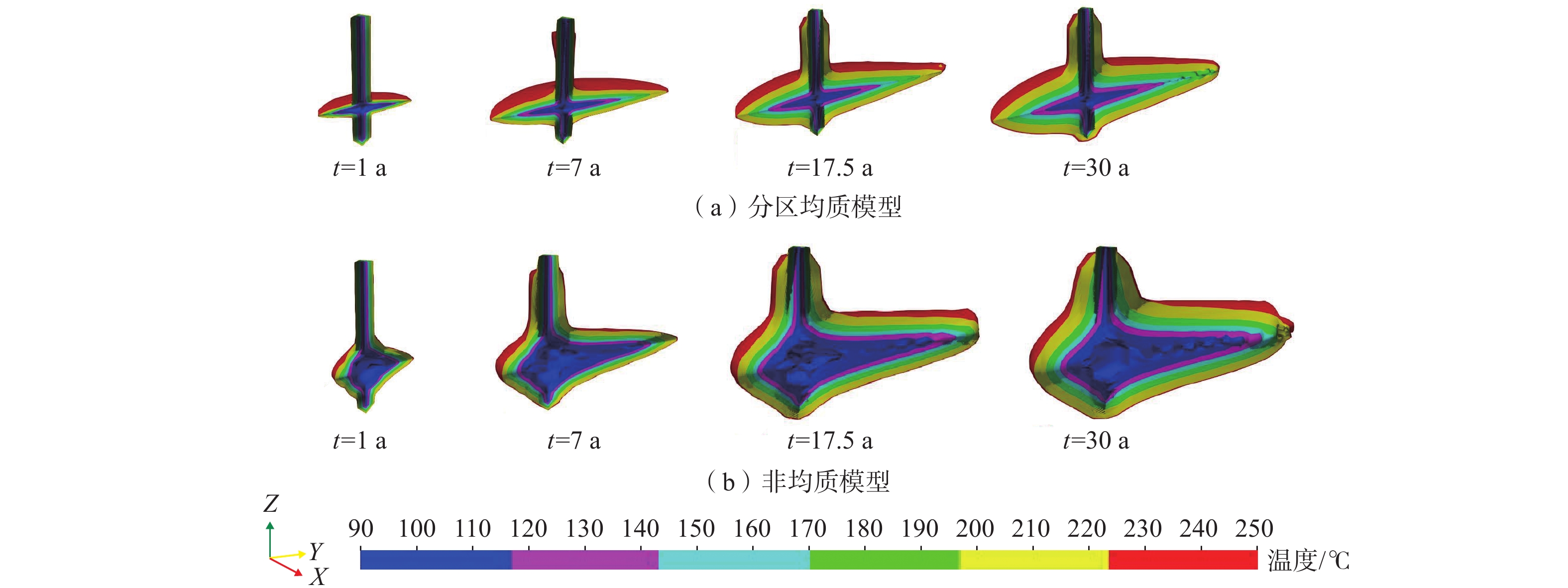
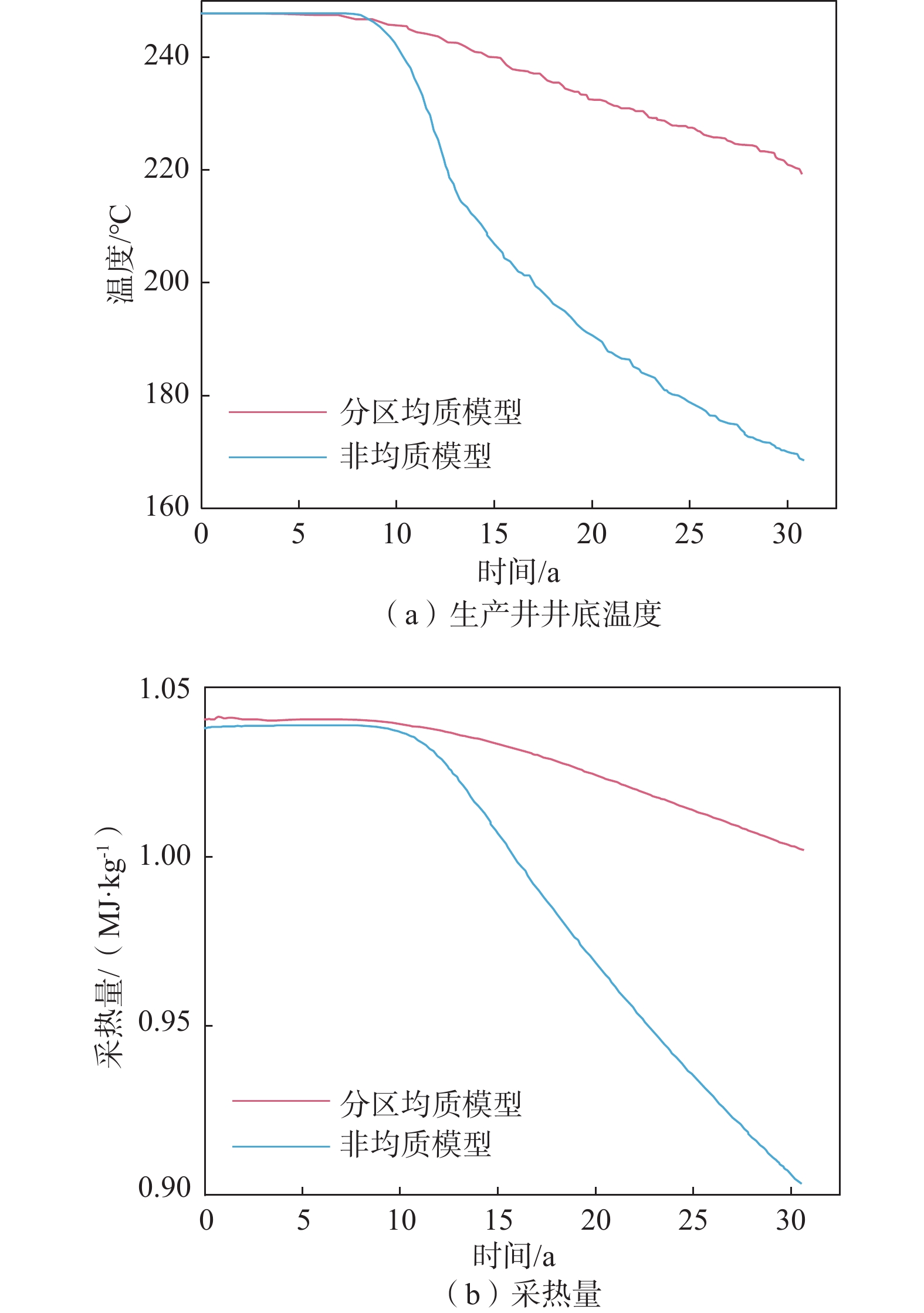
发展清洁、稳定、可再生的干热岩型地热资源对于缓解能源危机、减轻环境污染、改善人类健康具有重要意义。增强型地热系统(Enhanced Geothermal System,EGS) 是一项改造干热岩天然储层,高效开发地热能资源的先进技术。以澳大利亚库珀盆地地热储层为研究对象,基于水力压裂实测微震数据,建立了三维分区均质渗透率模型和非均质渗透率模型,分别进行储层温度场、流场及采热性能变化的研究,并对比其差异。结果表明:在同样的注采流量下,由于非均质模型中微震事件集中于井口附近,进而形成明显的优势流动通道,流体从注入井更快流向生产井,温度下降速度相对更快,分区均质模型中优势流动通道没有非均质模型明显,温度下降速度较慢;地热模型运行期间分区均质模型的采热量变化相对稳定,降幅为3.74%,非均质模型采热量降幅较大,为12.72%。分区均质模型的模拟结果相比于非均质模型,温度下降幅度小、采热量高;但实际储层中的渗透率分布不均,分区均质模型的模拟采热量相比实际采热量偏高,因此在实际应用中,非均质模型的模拟结果对实际工程更具参考意义。
Abstract:The development of clean, stable, and renewable hot dry rock geothermal energy is significant for alleviating the energy crisis, reducing environmental pollution, and improving human health. Enhanced geothermal system (EGS) is an advanced technology for developing geothermal energy efficiently by stimulating hot dry rock reservoir. This technology involves a complex hydro-thermal coupling process. A numerical approach is usually applied for analyzing heat extraction. In this paper, taking the geothermal reservoir of the Cooper basin in Australia as the research object, two models–a 3D zonal homogeneous permeability model and a heterogenious permeability model – are established based on the measured microseismic data of hydraulic fracturing. The latter one is inversed from microseismic data. The temperature field, seepage field and thermal performance of the reservoir are numerically studied, and their differences are compared and analyzed. The results show that with the same injection-production flow rate, fluid flows more quickly from the injection well to the production well while the temperature drops relatively more rapidly in the inhomogeneous model due to the dominant channel revealed by dense microseismic events near the wellbore. In the homogeneous model, the dominant flow channel is not as pronounced as in the previous model, and the temperature decreases more slowly. During the operation of the geothermal reservoir model, the change in heat recovery of the zonal homogeneous model is relatively stable, with a decline of 3.74%, and that of the inhomogeneous model is rather obvious, with a decline of 12.72%. Compared with the inhomogeneous model, a smaller temperature drop and a higher heat recovery exist in the homogeneous model. However, the permeability in the actual reservoir is uneven, and the simulated heat recovery of the zonal homogenization model is higher than the actual recovery. Therefore, the simulation results of the inhomogeneous model have more reference significance for practical engineering.
-
Key words:
- EGS /
- microseismic data /
- permeability /
- hydro-thermal coupling /
- numerical simulation
-

-
表 1 分区均质模型中岩石物理性质参数
Table 1. Parameters of rock in the zonal homogenization model
区域 密度
/(kg·m−3)比热
/(J·kg−1·K−1)孔隙度/% 导热系数
/(W·m−1·K−1)压缩系数
/(10−10 Pa−1)上层花岗岩 2 700 960 0.01 3.395 5.00 改造区 2 700 960 1.40 3.395 5.00 下层花岗岩 2 700 960 0.01 3.395 5.00 表 2 循环工作流体的物理性质参数
Table 2. Parameters of the circulating fluid
密度
/(kg·m−3)比热
/(J·kg−1·K−1)导热系数
/(W·m−1·K−1)黏度
/(Pa·s)压缩系数
/(10−10 Pa−1)水 1 000 4 200 0.6 0.001 5.0 表 3 分区均质模型不同渗透率下生产井中的模拟流量与实际流量
Table 3. Simulated flow and actual flow of production wells in the homogeneous model with different permeabilities
试验 渗透率/m2 时间/d 模拟流量/(m3·s−1) 实测流量/(m3·s−1) x y z 1 6.00×10−13 1.20×10−12 4.00×10−14 42 0.074 9 0.015 5 2 2.00×10−13 4.00×10−13 4.00×10−14 42 0.023 8 3 1.50×10−13 3.00×10−13 4.00×10−14 42 0.017 6 4 1.40×10−13 2.80×10−13 4.00×10−14 42 0.016 4 5 1.30×10−13 2.60×10−13 4.00×10−14 42 0.015 2 6 1.20×10−13 2.40×10−13 4.00×10−14 42 0.014 0 7 1.00×10−13 2.00×10−13 4.00×10−14 42 0.011 6 表 4 非均质模型不同渗透率相关参数下生产井中模拟流量与实际流量
Table 4. Simulated flow and actual flow of production wells in the heterogeneous model with different permeability related parameters
试验 渗透率计算相关系数 时间/d 模拟流量/(m3·s−1) 实测流量/(m3·s−1) B1 B2 B3 1 3.00×10-5 1.50×10-5 2.5 42 0.030 2 0.015 5 2 4.00×10-5 1.50×10-5 2.5 42 0.029 3 3 4.00×10-5 2.00×10-5 2.5 42 0.021 2 4 5.00×10-5 2.00×10-5 2.5 42 0.015 8 5 5.00×10-5 2.50×10-5 2.5 42 0.008 6 -
[1] SUN Z X,ZHANG X,XU Y,et al. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model[J]. Energy,2017,120:20 − 33. doi: 10.1016/j.energy.2016.10.046
[2] XU C S,DOWD P A,TIAN Z F. A simplified coupled hydro-thermal model for enhanced geothermal systems[J]. Applied Energy,2015,140:135 − 145. doi: 10.1016/j.apenergy.2014.11.050
[3] 许天福,张炜. 增强型地热工程国际发展和我国前景展望[J]. 石油科学通报,2016,1(1):38 − 44. [XU Tianfu,ZHANG Wei. Enhanced geothermal systems:International developments and China’s prospects[J]. Petroleum Science Bulletin,2016,1(1):38 − 44. (in Chinese with English abstract)
[4] WANG Y,LI T,CHEN Y,et al. A three-dimensional thermo-hydro-mechanical coupled model for enhanced geothermal systems (EGS) embedded with discrete fracture networks[J]. Computer Methods in Applied Mechanics and Engineering,2019,356:465 − 489. doi: 10.1016/j.cma.2019.06.037
[5] OLASOLO P,JUÁREZ M C,MORALES M P,et al. Enhanced geothermal systems (EGS):A review[J]. Renewable and Sustainable Energy Reviews,2016,56:133 − 144. doi: 10.1016/j.rser.2015.11.031
[6] JIANG F M,CHEN J L,HUANG W B,et al. A three-dimensional transient model for EGS subsurface thermo-hydraulic process[J]. Energy,2014,72:300 − 310. doi: 10.1016/j.energy.2014.05.038
[7] ALIYU M D,ARCHER R A. Numerical simulation of multifracture HDR geothermal reservoirs[J]. Renewable Energy,2021,164:541 − 555. doi: 10.1016/j.renene.2020.09.085
[8] 段云星, 杨浩. 增强型地热系统采热性能影响因素分析[J]. 吉林大学学报(地球科学版),2020,50(4):1161 − 1172. [DUAN Yunxing, YANG Hao. Analysis of influencing factors on heat extraction performance of enhanced geothermal system[J]. Journal of Jilin University (Earth Science Edition),2020,50(4):1161 − 1172. (in Chinese with English abstract)
[9] XING H L, GAO J, ZHANG J, et al. Towards an integrated simulator for enhanced geothermal reservoirs[C]//35th Stanford Geotherma Workshop. Bali: Indonesia, 2010: 25 − 29.
[10] XING H L,LIU Y,GAO J F,et al. Recent development in numerical simulation of enhanced geothermal reservoirs[J]. Journal of Earth Science,2015,26(1):28 − 36. doi: 10.1007/s12583-015-0506-2
[11] AYLING B F,HOGARTH R A,ROSE P E. Tracer testing at the Habanero EGS site,central Australia[J]. Geothermics,2016,63:15 − 26. doi: 10.1016/j.geothermics.2015.03.008
[12] LLANOS E M,ZARROUK S J,HOGARTH R A. Numerical model of the Habanero geothermal reservoir,Australia[J]. Geothermics,2015,53:308 − 319. doi: 10.1016/j.geothermics.2014.07.008
[13] HOGARTH, BOUR, DANIEL. Flow Performance of the Habanero EGS Closed Loop[R]. Melbourne: World Geothermal Congress, 2015.
[14] SAMIN M Y,FARAMARZI A,JEFFERSON I,et al. A hybrid optimisation approach to improve long-term performance of enhanced geothermal system (EGS) reservoirs[J]. Renewable Energy,2019,134:379 − 389. doi: 10.1016/j.renene.2018.11.045
[15] 李庭樑,黄文博,曹文炅,等. EGS热储基于微震数据反演模化及其采热性能分析[J]. 化工学报,2018,69(12):5001 − 5010. [LI Tingliang,HUANG Wenbo,CAO Wenjiong,et al. Inverse modeling of EGS heat reservoir based on micro-seismic data and analysis of its heat recovery performance[J]. CIESC Journal,2018,69(12):5001 − 5010. (in Chinese with English abstract)
[16] YAO C,SHAO Y L,YANG J H. Numerical investigation on the influence of areal flow on EGS thermal exploitation based on the 3-D T-H single fracture model[J]. Energies,2018,11(11):1 − 19.
[17] LI T Y,HAN D X,YANG F S,et al. Modeling study of the thermal-hydraulic-mechanical coupling process for EGS based on the framework of EDFM and XFEM[J]. Geothermics,2021,89:101953. doi: 10.1016/j.geothermics.2020.101953
[18] XU C, DOWD P, MOHAIS R. Connectivity analysis of the Habanero enhanced geothermal system[R]. Stanford: The 37th Workshop on Geothermal Reservoir Engineering, 2012.
[19] FANG Y,ELSWORTH D,CLADOUHOS T T. Reservoir permeability mapping using microearthquake data[J]. Geothermics,2018,72:83 − 100. doi: 10.1016/j.geothermics.2017.10.019
[20] XING H L. Finite element simulation of transient geothermal flow in extremely heterogeneous fractured porous media[J]. Journal of Geochemical Exploration,2014,144:168 − 178. doi: 10.1016/j.gexplo.2014.03.002
[21] WYBORN D. Update of development of the geothermal field in the granite at innamincka, south Australia[R]. Bali: World Geothermal Congress, 2012.
[22] XU C S,DOWD P,LI Q. Carbon sequestration potential of the Habanero reservoir when carbon dioxide is used as the heat exchange fluid[J]. Journal of Rock Mechanics and Geotechnical Engineering,2016,8(1):50 − 59. doi: 10.1016/j.jrmge.2015.05.003
[23] BAISCH S,WEIDLER R,VOROS R,et al. Induced seismicity during the stimulation of a geothermal HFR reservoir in the Cooper Basin,Australia[J]. Bulletin of the Seismological Society of America,2006,96(6):2242 − 2256. doi: 10.1785/0120050255
[24] HILLIS R,HAND M,MILDREN S,et al. Hot dry rock geothermal exploration in Australia[J]. ASEG Extended Abstracts,2004,2004(1):1 − 4.
[25] BAISCH S,VOROS R,WEIDLER R,et al. Investigation of fault mechanisms during geothermal reservoir stimulation experiments in the cooper basin,Australia[J]. Bulletin of the Seismological Society of America,2009,99(1):148 − 158. doi: 10.1785/0120080055
[26] O’SULLIVAN M J, O’SULLIVAN J P. Reservoir modeling and simulation for geothermal resource characterization and evaluation[C]//Geothermal Power Generation. Amsterdam: Elsevier, 2016: 165 − 199.
[27] 白斌. THM耦合作用对储层孔渗参数影响及地热系统优化研究[D]. 青岛: 中国石油大学(华东), 2018
BAI Bin. Research on hydrodynamic parameters in rock reservoir and optimization of geothermal system with THM coupling[D]. Qingdao: China University of Petroleum (Huadong), 2018. (in Chinese with English abstract)
[28] XU G X, WANG S Z. Numerical investigation of fluid flow and heat transfer in a two dimensional anisotropic EGS model[C]//International Conference on Industrial Engineering & Applications. Toronto: IEEE, 2017: 372 − 375.
-




 下载:
下载: