An experimental study of the stress-strain relationship of different excavation paths for soft soil K0 consolidation
-
摘要:
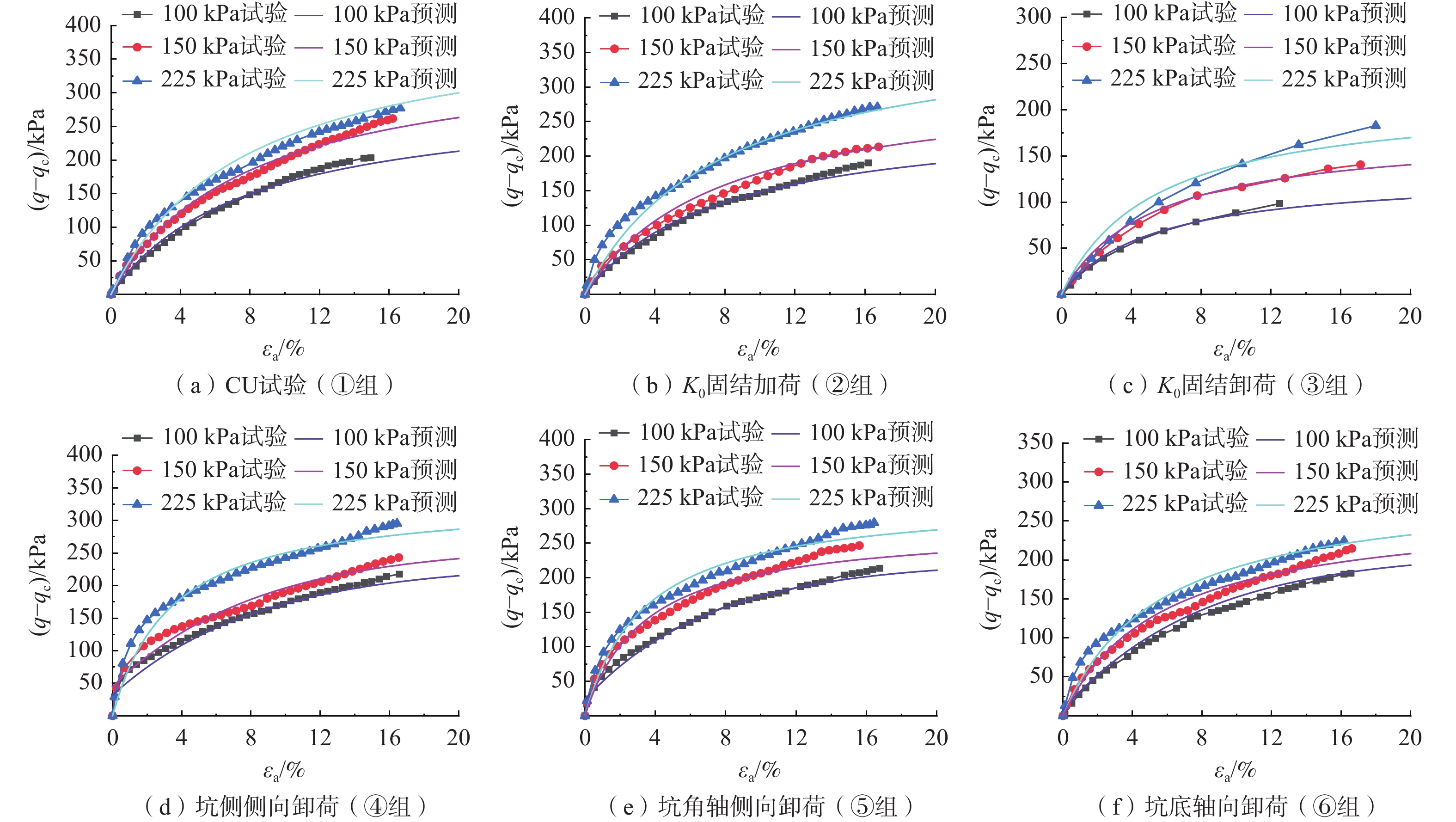
基坑开挖过程中不同部位的土体会因不同的卸荷力学行为而表现出动态的破坏特性。为研究基坑土体开挖过程中复杂的卸荷应力路径,利用TSZ-1S应力控制式三轴仪分别对湖相沉积的泥炭质土进行固结不排水及K0固结下的加、卸荷试验,并按侧向、轴向、轴侧向同时卸荷等不同卸荷条件制定试验方案,模拟基坑开挖过程中不同部位土体卸荷路径下的应力-应变曲线、卸荷剪切破坏时的强度及初始切线模量等的变化规律。试验结果表明:土体的应力-应变特性与应力路径密切相关,各路径下应力-应变曲线都近似呈双曲线型;卸荷剪切破坏时强度明显低于加荷破坏。对不同卸荷路径下初始切线模量(Ei)的研究发现,Ei受侧向卸荷影响较大,卸荷后Ei有所提高,轴向卸荷对其影响较小。对各应力-应变曲线进行归一化处理,构建了考虑不同归一化因子的归一化方程,以该方程为基础对不同应力路径下的泥炭质土进行归一化处理,并对结果进行了验证,效果良好。本研究可为泥炭质土场地上基坑在不同卸荷路径下的变形参数和本构关系的研究提供参考。
Abstract:In the process of foundation pit excavation, the soil mass in different parts shows dynamic destruction characteristics due to diverse unloading mechanics. In order to study the complex unloading stress path in the foundation excavation, the TSZ-1S stress control triaxial compression apparatus is used to carry out the loading and unloading tests of the lacustrine sedimentary peat soil under the conditions of consolidation undrained and K0 consolidation, respectively, and the test scheme is formulated according to different unloading conditions such as lateral, axial and axial lateral meantime unloading, so as to simulate the stress-strain curves of soil under different unloading paths in the foundation excavation and the variation laws of strength and initial tangent modulus under unloading shear failure. The test results show that the stress-strain characteristics of soil are closely related to the stress path, and the stress-strain curves under each path are approximately hyperbolic. The strength of unloading shear failure is significantly lower than that of loading failure. The study of initial tangent modulus Ei under different unloading paths shows that Ei is greatly affected by lateral unloading, Ei increases after unloading, and axial unloading has little effect on it. The stress-strain curves are normalized, and the normalization equation of peat soil considering different normalization factors is constructed. Based on this equation, the peat soil under different stress paths is normalized, and the results are verified. The results of this work can provide reference for the study of deformation parameters and constitutive relations of foundation pits on peat soil sites under different unloading paths.
-
Key words:
- peat soil /
- unloading path /
- K0 consolidation /
- stress-strain /
- starting tangent modulus /
- normalization
-

-
表 1 不同卸荷路径下三轴剪切试验方案
Table 1. Triaxial shear test schemes under different unloading paths
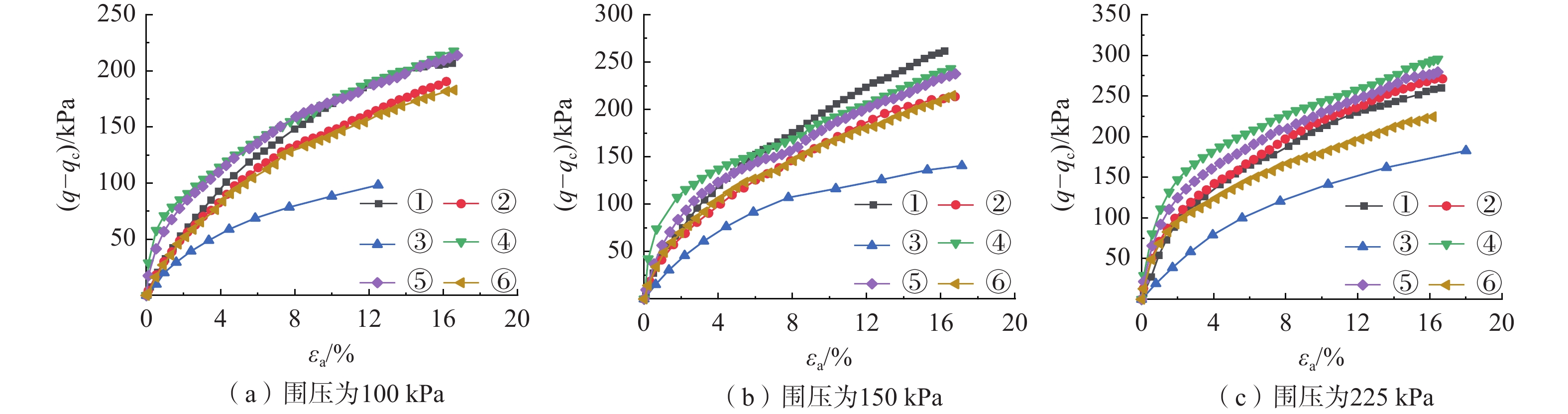
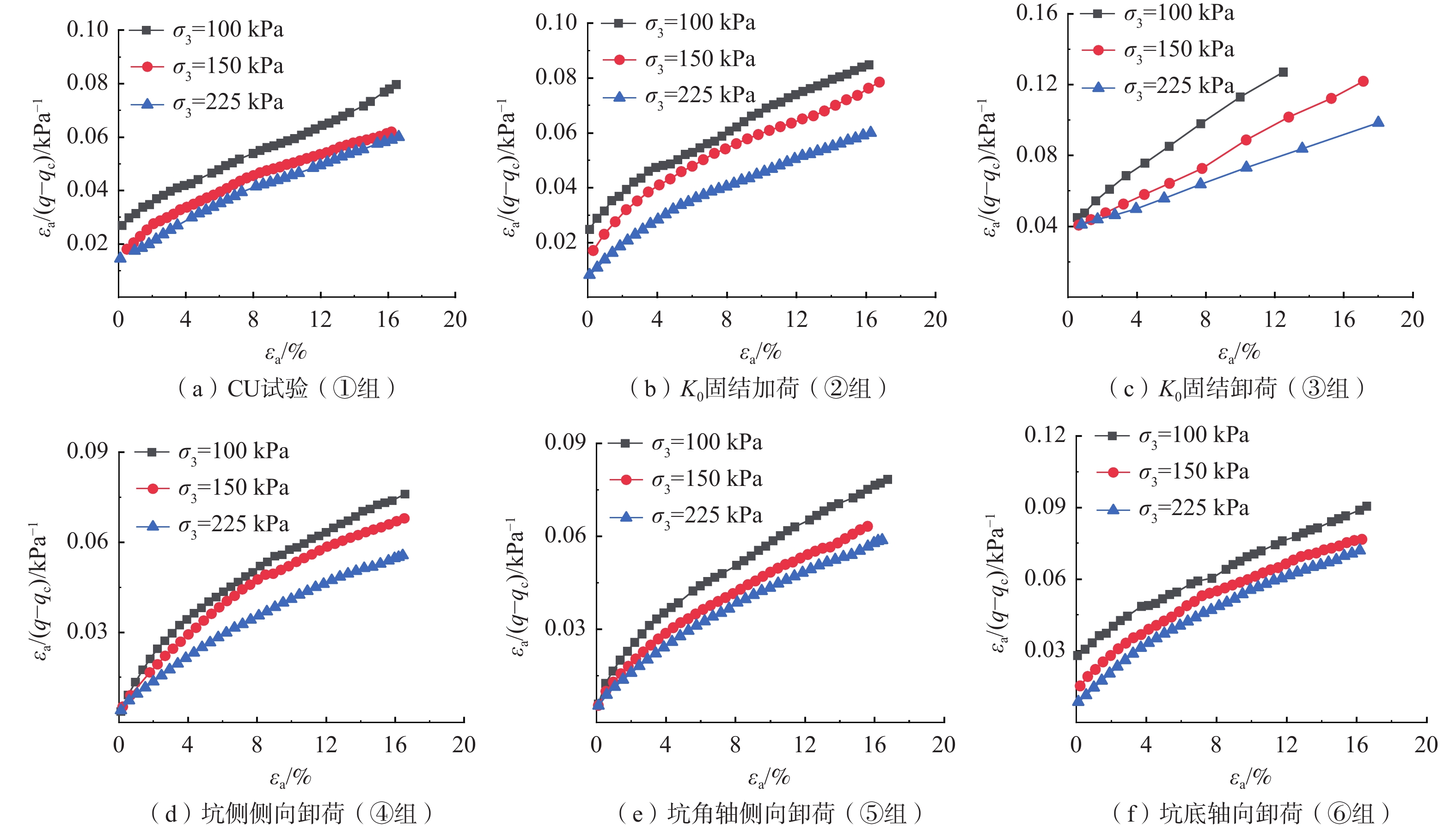
试验分组 σ3/kPa 固结方式 卸荷路径 剪切路径 ① 100 等向固结 无 σ3不变,σ1
逐渐增大150 225 ② 100 K0固结 无 150 225 ③ 100 K0固结 σ3每级减10 kPa至破坏 σ1不变,σ3
逐渐减小150 σ3每级减15 kPa至破坏 225 σ3每级减20 kPa至破坏 ④ 100 K0固结 σ3=100→90→80→70→
60→80→100σ3不变,σ1
逐渐增大150 σ3=150→135→120→
105→90→120→150225 σ3=225→205→185→
165→145→185→225⑤ 100 K0固结 每级σ3变化与④组一致,σ3减小时沿K0线减小σ1,后恢复至初始状态 150 225 ⑥ 100 K0固结 σ1=133→128→123→
118→113→123→133150 σ1=200→192→185→
177→170→185→200225 σ1=300→290→280→
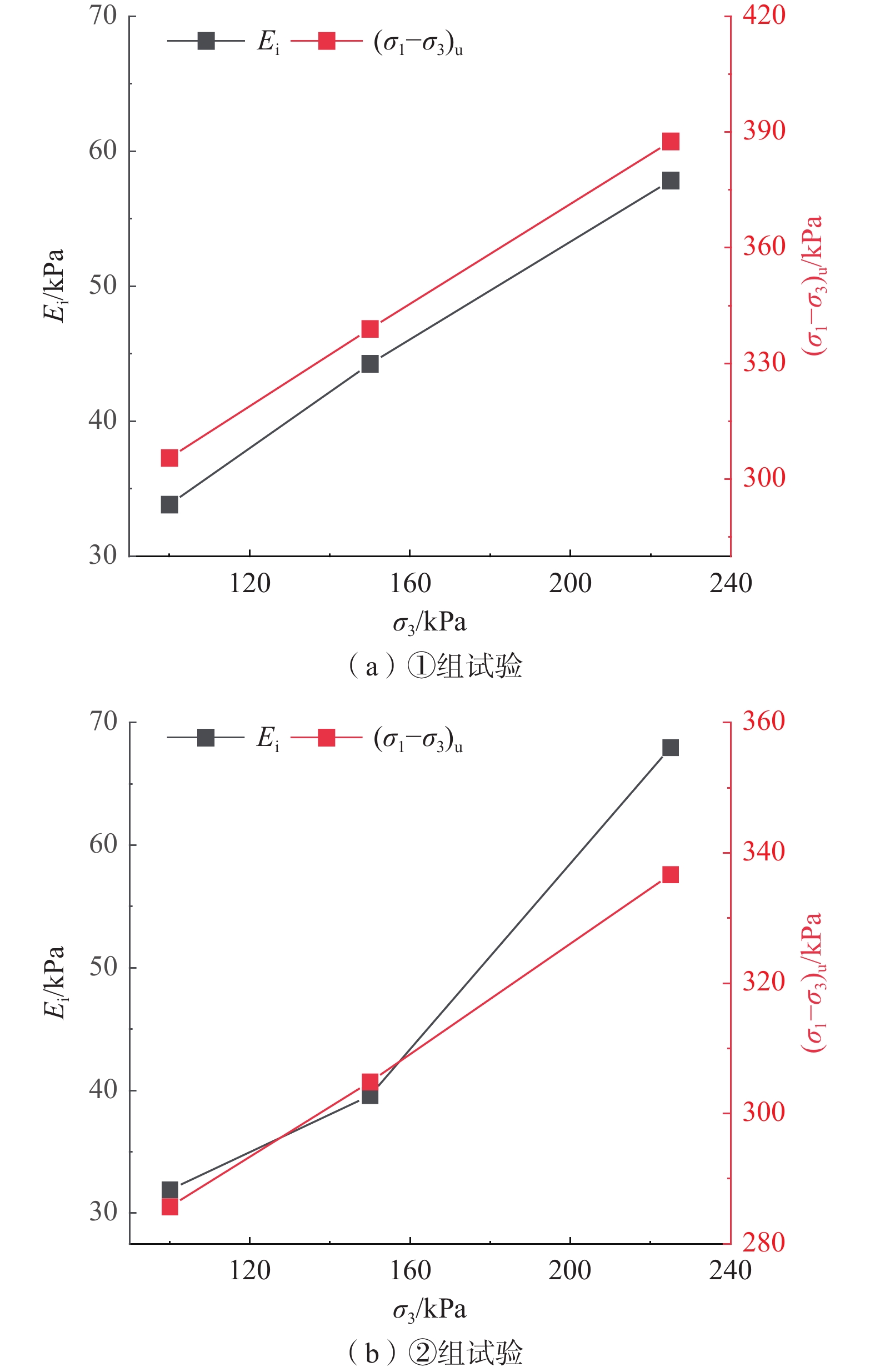
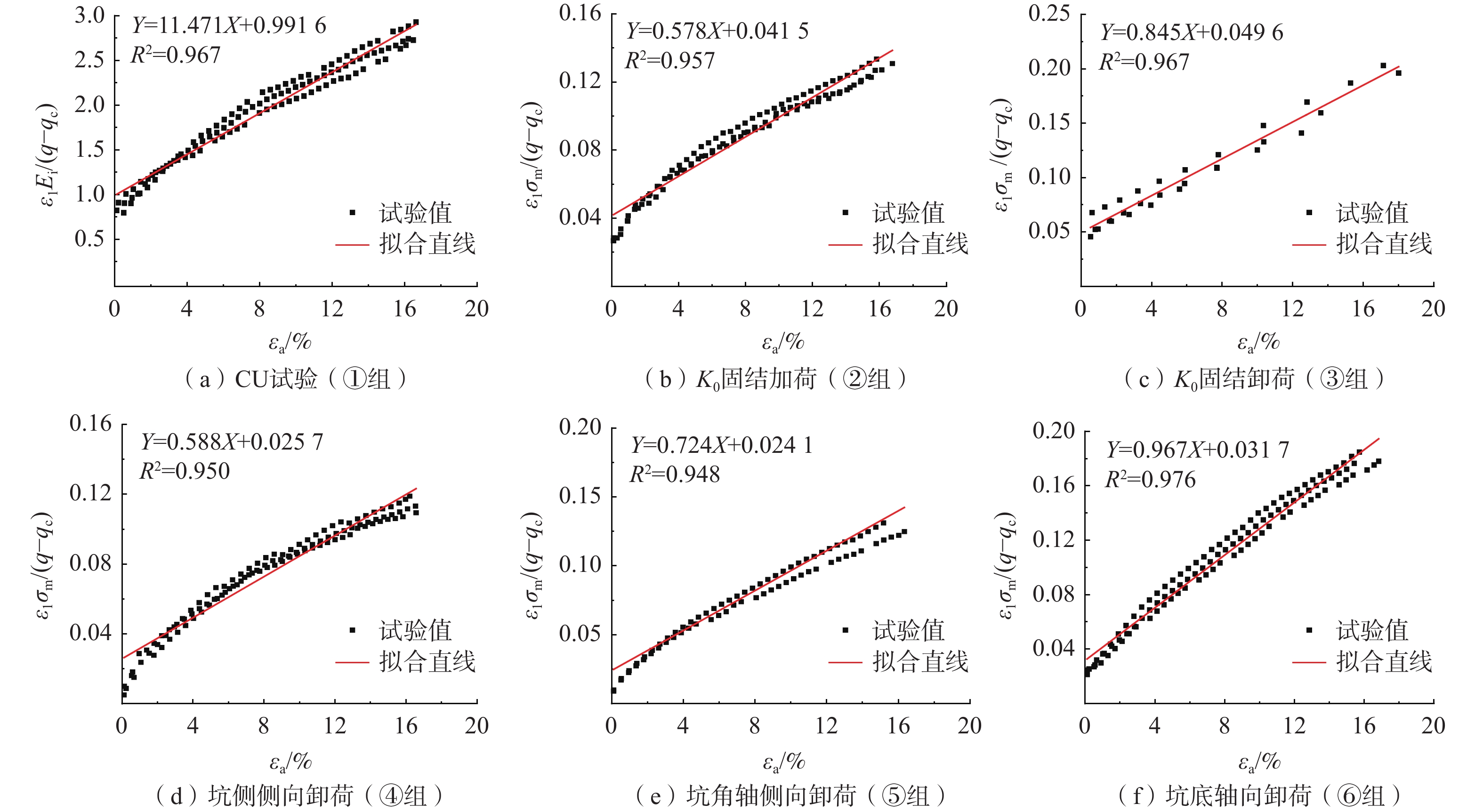
270→260→280→300注:σ1、σ3分别表示大、小主应力。 表 2 Ei与σm拟合表达式及参数值
Table 2. Ei and σm fitting expressions and parameter values
试验组 σm/kPa Ei/MPa R2 表达式 ① 100 33.84 0.998 
150 44.27 225 57.84 ② 111 31.91 0.958 
167 39.60 250 67.98 ③ 111 23.02 0.986 
167 27.37 250 31.68 ④ 111 62.77 0.945 
167 69.69 250 110.87 ⑤ 111 57.01 0.947 
167 75.76 250 88.18 ⑥ 111 30.62 0.999 
167 43.98 250 64.31 -
[1] LAMBE W T. Stress path method[J]. Journal of the Soil Mechanics and Foundations Division,1967,93(6):309 − 331. doi: 10.1061/JSFEAQ.0001058
[2] 李立云, 王子英, 王晓静, 等. 近铁路基坑通风井段变形特征及其机制分析. 吉林大学学报(地球科学版), 2021, 51(5): 1441 − 1451.
LI Liyun, WANG Ziying, WANG Xiaojing, et al. Study on deformation characteristics of ventilation shaft section in foundation pit xxcavation adjacent to railway. Journal of Jilin University (Earth Science Edition), 2021, 51(5): 1441 − 1451.(in Chinese with English abstract)
[3] 陈善雄,凌平平,何世秀,等. 粉质黏土卸荷变形特性试验研究[J]. 岩土力学,2007,28(12):2534 − 2538. [CHEN Shanxiong,LING Pingping,HE Shixiu,et al. Experimental study on deformation behavior of silty clay under unloading[J]. Rock and Soil Mechanics,2007,28(12):2534 − 2538. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-7598.2007.12.009
[4] HSIEH P G, OU C Y. Analysis of nonlinear stress and strain in clay under the undrained condition[J]. Journal of Mechanics, 2011, 27(2): 201 − 213.
[5] 李德宁, 楼晓明, 杨敏. 上海地区基坑开挖卸荷土体回弹变形试验研究[J]. 岩土力学, 2011, 32(增刊2): 244 − 249
LI Dening, LOU Xiaoming, YANG Min. Experimental researches on unloading resilient deformation properties during excavations in Shanghai area[J]. Rock and Soil Mechanics, 2011, 32(Sup2): 244 − 249. (in Chinese with English abstract)
[6] 张玉, 邵生俊. 平面应变加、卸荷条件下黄土的非线性变形特性的研究[J]. 岩土工程学报, 2015, 37(增刊1): 185 − 190
ZHANG Yu, SHAO Shengjun. Non-linear deformation behaviors of loess under plane strain state of vertical loading and lateral unloading[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(Sup1): 185 − 190. (in Chinese with English abstract)
[7] 杨爱武,杨少坤,张振东. 基于不同卸荷速率与路径影响下吹填土力学特性研究[J]. 岩土力学,2020,41(9):2891 − 2900. [YANG Aiwu,YANG Shaokun,ZHANG Zhendong. Experimental study of mechanical properties of dredger fill under different unloading rates and stress paths[J]. Rock and Soil Mechanics,2020,41(9):2891 − 2900. (in Chinese with English abstract) doi: 10.16285/j.rsm.2019.1992
[8] 李新明,孔令伟,郭爱国. 考虑卸荷速率的K0固结膨胀土应力-应变行为[J]. 岩土力学,2019,40(4):1299 − 1306. [LI Xinming,KONG Lingwei,GUO Aiguo. Stress-strain behavior of expansive soil under K0 condition with different unloading rates[J]. Rock and Soil Mechanics,2019,40(4):1299 − 1306. (in Chinese with English abstract)
[9] 梅国雄,陈浩,卢廷浩,等. 坑侧土体卸荷的侧向应力-应变关系研究[J]. 岩石力学与工程学报,2010,29(增刊1):3108 − 3112. [MEI Guoxiong,CHEN Hao,LU Tinghao,et al. Research on lateral stress-strain relation on side of foundation pit with lateral unloading[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(Sup1):3108 − 3112. (in Chinese with English abstract)
[10] 陈志波,钟理峰,蔡廉锦,等. 基坑开挖过程坑侧土体应力路径试验研究[J]. 防灾减灾工程学报,2016,36(6):943 − 949. [CHEN Zhibo,ZHONG Lifeng,CAI Lianjin,et al. Stress pathtriaxial tests on the lateral soil of foundation pit during excavation process[J]. Journal of Disaster Prevention and Mitigation Engineering,2016,36(6):943 − 949. (in Chinese with English abstract) doi: 10.13409/j.cnki.jdpme.2016.06.014
[11] 陈立国,吴昊天,陈晓斌,等. 超载预压处理软土的次固结特征及沉降计算[J]. 水文地质工程地质,2021,48(1):138 − 145. [CHEN Liguo,WU Haotian,CHEN Xiaobin,et al. Secondary consolidation characteristics and settlement calculation of soft soil treated by overload preloading[J]. Hydrogeology & Engineering Geology,2021,48(1):138 − 145. (in Chinese with English abstract) doi: 10.16030/j.cnki.issn.1000-3665.202009016
[12] 孟凡丽,娄桢桢,葛威. 长期循环荷载下卸荷粉土动力特性的试验研究[J]. 岩土力学,2022,43(增刊1):383 − 388. [MENG Fanli,LOU Zhenzhen,GE Wei. Experimental study on dynamic characters of unloading silt under long-term cyclic loading[J]. Rock and Soil Mechanics,2022,43(Sup1):383 − 388. (in Chinese with English abstract) doi: 10.16285/j.rsm.2021.0106
[13] BALASUBRAMANIAM A S,CHAUDRY A R. Deformation and strength characteristics of soft bangkok clay[J]. Journal of the Geotechnical Engineering Division,1978,104(9):1153 − 1167. doi: 10.1061/AJGEB6.0000685
[14] 李作勤. 粘土归一化性状的分析[J]. 岩土工程学报,1987,9(5):67 − 75. [LI Zuoqin. Analysis of normalized properties of clay[J]. Chinese Journal of Geotechnical Engineering,1987,9(5):67 − 75. (in Chinese with English abstract) doi: 10.3321/j.issn:1000-4548.1987.05.008
[15] 曾国熙. 正常固结黏土不排水剪切的归一化性状[C]//软土地基学术讨论会论文集. 北京: 水利出版社, 1980: 13 − 26
ZENG Guoxi. Normalized properties of normally consolidated clay soils in undrained shear[C]// Proceedings of the Symposium on Soft Ground Foundation. Beijing: Water Resources Press, 1980: 13 − 26. (in Chinese with English abstract)
[16] 余志华,桂跃,付坚,等. 轴向卸荷条件下泥炭质土回弹变形试验研究[J]. 水文地质工程地质,2015,42(5):107 − 114. [YU Zhihua,GUI Yue,FU Jian,et al. An experimental study of the rebound deformation characteristics and mechanism of peaty soil under unloading[J]. Hydrogeology & Engineering Geology,2015,42(5):107 − 114. (in Chinese with English abstract) doi: 10.16030/j.cnki.issn.1000-3665.2015.05.18
[17] 吴昳,朱俊高,黄浩然,等. 不同密度粉质粘土K0固结侧向卸荷三轴试验研究[J]. 河北工程大学学报(自然科学版),2022,39(3):49 − 55. [WU Yi,ZHU Jungao,HUANG Haoran,et al. Triaxial test study on K0 consolidation of different density silty clays with lateral unloading[J]. Journal of Hebei University of Engineering (Natural Science Edition),2022,39(3):49 − 55. (in Chinese with English abstract) doi: 10.3969/j.issn.1673-9469.2022.03.008
[18] 周洪福,冯治国,石胜伟,等. 川藏铁路某特大桥成都侧岸坡工程地质特征及稳定性评价[J]. 水文地质工程地质,2021,48(5):112 − 119. [ZHOU Hongfu,FENG Zhiguo,SHI Shengwei,et al. Slope engineering geology characteristics and stability evaluationof a grand bridge to Chengdu bank on the Sichuan-Xizang Railway[J]. Hydrogeology & Engineering Geology,2021,48(5):112 − 119. (in Chinese with English abstract) doi: 10.16030/j.cnki.issn.1000-3665.202103076
[19] 中华人民共和国住房和城乡建设部. 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019
Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for geotechnical testing method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[20] 苟富刚,龚绪龙,陆徐荣,等. 有机质对海相软土物理力学特性的影响效应分析[J]. 水文地质工程地质,2022,49(5):195 − 203. [GOU Fugang,GONG Xulong,LU Xurong,et al. Effect of organic matter content on physical-mechanical properties of sea soft soil[J]. Hydrogeology & Engineering Geology,2022,49(5):195 − 203. (in Chinese with English abstract) doi: 10.16030/j.cnki.issn.1000-3665.202109033
[21] KONDNER R L. Hyperbolic stress-strain response:Cohesive soils[J]. Journal of the Soil Mechanics and Foundations Division,1963,89(1):115 − 143. doi: 10.1061/JSFEAQ.0000479
[22] 刘熙媛. 基坑开挖过程的试验与数值模拟及土的微观结构研究[D]. 天津: 天津大学, 2004
LIU Xiyuan. Experimental and numerical simulation of excavation process and microstructure study[D]. Tianjin: Tianjin University, 2004. (in Chinese with English abstract)
[23] 蒋海飞,刘东燕,黄伟,等. 高围压下不同孔隙水压作用时岩石蠕变特性及改进西原模型[J]. 岩土工程学报,2014,36(3):443 − 451. [JIANG Haifei,LIU Dongyan,HUANG Wei,et al. Creep properties of rock under high confining pressure and different pore water pressures and a modified Nishihara model[J]. Chinese Journal of Geotechnical Engineering,2014,36(3):443 − 451. (in Chinese with English abstract)
[24] 张挺,彭世龙,曹广勇,等. 膨胀土侧向卸荷试验研究及归一化特性分析[J]. 水利水电技术(中英文),2023,54(1):175 − 186. [ZHANG Ting,PENG Shilong,CAO Guangyong,et al. Experimental study on lateral unloading of expansive soil and analysis of normalized characteristics[J]. Water Resources and Hydropower Engineering,2023,54(1):175 − 186. (in Chinese with English abstract)
[25] 郭小帅. 基坑开挖中土体侧向卸荷特性研究[D]. 北京: 北京交通大学, 2012
GUO Xiaoshuai. Research on the lateral unloading behavior of soils in deep excavation[D]. Beijing: Beijing Jiaotong University, 2012. (in Chinese with English abstract)
[26] 周秋娟,陈晓平. 侧向卸荷条件下软土典型力学特性试验研究[J]. 岩石力学与工程学报,2009,28(11):2215 − 2221. [ZHOU Qiujuan,CHEN Xiaoping. Test research on typical mechanical characteristics of soft clay under lateral unloading condition[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(11):2215 − 2221. (in Chinese with English abstract)
[27] 王大雁,马巍,常小晓,等. 深部人工冻土在小应变条件下的刚度特性[J]. 岩土力学,2006,27(9):1447 − 1451. [WANG Dayan,MA Wei,CHANG Xiaoxiao,et al. Small-strain stiffness properties of frozen soils in deep alluvium[J]. Rock and Soil Mechanics,2006,27(9):1447 − 1451. (in Chinese with English abstract) doi: 10.16285/j.rsm.2006.09.003
[28] VARDANEGA P J,BOLTON M D. Stiffness of clays and silts:Normalizing shear modulus and shear strain[J]. Journal of Geotechnical and Geoenvironmental Engineering,2013,139(9):1575 − 1589. doi: 10.1061/(ASCE)GT.1943-5606.0000887
[29] 谢飞. 基于结构性力学参数的黄土归一化性状研究: 以延安地区马兰黄土为例[D]. 西安: 长安大学, 2021
XIE Fei. Research on the normalized properties of loess based on structural parameters— A case of Malan loess in Yan’an area[D]. Xi’an: Chang’an University, 2021. (in Chinese with English abstract)
-




 下载:
下载: